标签:最优 证明 alt idt lazy ora 要求 line load
一. 算法思想
在使用best-first的搜索策略时,有时可以得到最优解,有时无法得到最优解,因此best-first只能较快的解决可行解问题。
A*算法是 重新定义代价函数,使得best-first搜索策略可以得到优化解的算法
A*算法(Best-first + 特殊代价函数~> 优化解)
a. 设计g(n)、h(n)、f(n):(带*为实际值,不带*为估计值)
g(n)=从树根到n的代价(原best-first中的代价函数)
h(n)=n到目标节点优化代价估计值(【要求】:新构造的估计函数,满足:h(n)<=h*(n) )
f(n)=g(n)+ h(n)是节点n的估计代价(A*算法的估计代价函数,满足f(n)<=f*(n) )
思想:抵达目标结点时,同时满足
(1)算法本身保证的估计值始终小于等于最优解
(2)作为可行解始终大于等于最优解
b. 根据best-first搜索策略即可得到优化解
二. 正确性证明
证明:A*算法得到的解一定是优化解
令n是任意扩展到的节点, t 是第一个抵达的目标结点.
往证:当f(t)=g(t)时,即得到优化解代价.
(1)A*算法使用Best-first策略, f(t) <= f(n)
(2).A*算法使用h(n)<=h*(n)估计规则, f(t)<=f(n)<=f*(n).
(3). {f*(n)}中必有一个为优化解的代价,令其为f*(s). 我们有f(t) <= f*(s).
(4). t是目标节点h(t)=0,所以f(t)=g(t)+h(t)=g(t) <= f*(s).
(5). f(t)=g(t)是一个可能解,g(t) >= f*(s),f(t)=g(t)=f*(s).
三. 算法应用
【最短路径问题】
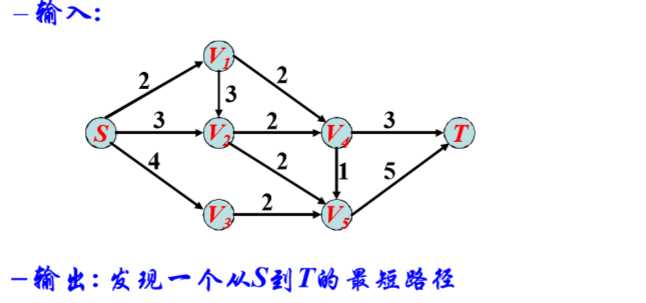
(1)设计g(n)、 h(n):
g(n):出发点到当前点的代价(构造时参考best-first策略)
h(n):当前点的最小出边权值(构造时只需满足h(n) <= h*(n)即可)
(2)Best-first策略得到最优解即可
标签:最优 证明 alt idt lazy ora 要求 line load
原文地址:https://www.cnblogs.com/duanshuai/p/13187568.html