C语言 汉诺塔问题

标签：font   写代码   ima   microsoft   style   char   size   span   汉诺塔问题   

汉诺塔运用到了分治的思想，把一个完整的塔给拆分成了两个部分：

假设一个塔有n各部分，那么将其分为两个部分：前n-1块为上半部分，第n个(即最下面一个为下半部分)

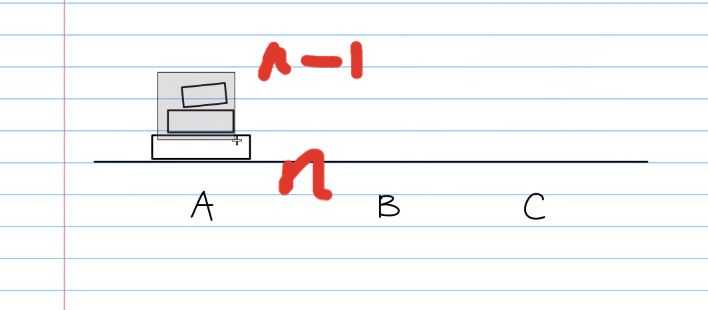
想要把上下两层的汉诺塔完整的移动到第三个轴处，只需要将上一层(n-1层)先从A柱借助C柱移动到B柱，然后把下半层(n层)移动到C柱，最后将放在B柱上的n-1层借助A柱放到C柱上，那么整个过程就成功了

第一步，先将上面n-1层（假设一共有n层）借助C柱全部放到B上：因为上层必须经过C才能按上小下大的顺序全部放到B上，所以这里强调必须经过C柱。

伪代码可表示为:hanoi(n-1,A,C,B)//n-1层从A借助C移动到B

第一步 移动结束：

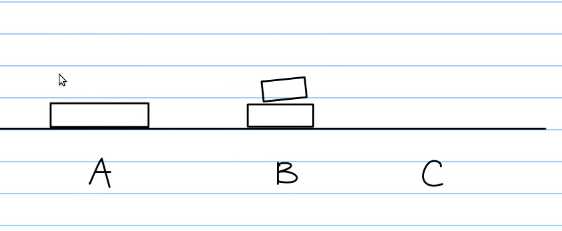
第二步：把A柱剩下的最大块直接移动到C柱:伪代码就相当于move(A,C)

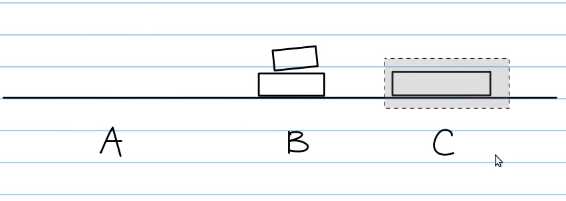
 第三步：把B柱的n-1层借助A柱全部按上小下大移动到C上面(必须说明的是因为B上的n-1块板子如要按照上小下大的顺序完整的移动到C上面一定是要经过A这个柱子的。从分治的角度出发说明，中间的某些块必定要经过B，只是由于把整体分成了两大块所以忽视了，但是写代码的时候一定是要写上的)

伪代码可表示为hanoi(n-1,B,A,C)

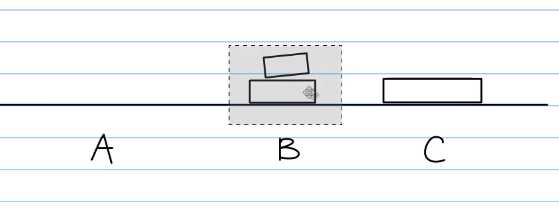
 中间必定会从A再到C

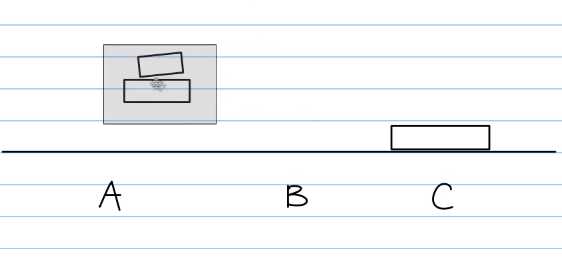
落到A以后再到C

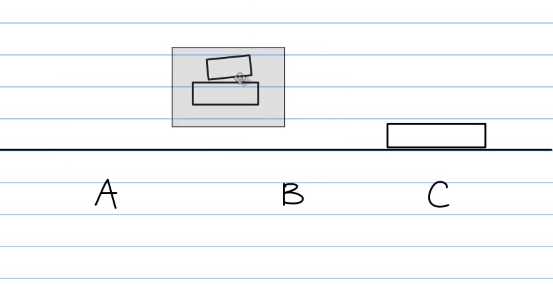
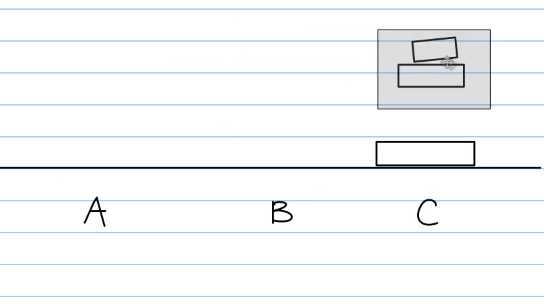
 这就是完整的汉诺塔移动规律

 代码可以写为

#include<stdio.h>
void hanoi(int n,char A,char B,char C)
{
    if(n==1)
        printf("%c->%c\n",A,C);//递归出口，如只有一个块，直接从A到C就可以了 
    else
    {
        hanoi(n-1,A,C,B);//首先把n-1块板子们全部从A借助C移动到B 
        printf("%c->%c\n",A,C);//接着再把处于A的第n层移动到C 
        hanoi(n-1,B,A,C);//最后再把处于B的n-1块板子们借助A全部移动到C 
    }//汉诺塔完成 
}
int main()
{
    hanoi(3,‘A‘,‘B‘,‘C‘);
    return 0;
}

C语言 汉诺塔问题

标签：font   写代码   ima   microsoft   style   char   size   span   汉诺塔问题   

原文地址：https://www.cnblogs.com/oldfish123/p/13209494.html