标签：指针 循环输出 最大 种类型 大小 bit 二进制 linux data-
在探求为何机器要使用补码之前, 让我们先了解原码, 反码和补码的概念.对于一个数, 计算机要使用一定的编码方式进行存储. 原码, 反码, 补码是机器存储一个具体数字的编码方式.
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:
[+1]原 = 0000 0001 [-1]原 = 1000 0001
第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:
[1111 1111 , 0111 1111]==>[-127 , 127]
反码的表示方法是:
[+1] = [00000001]原 = [00000001]反 [-1] = [10000001]原 = [11111110]反
补码的表示方法是:
[+1] = [00000001]原 = [00000001]反 = [00000001]补 [-1] = [10000001]原 = [11111110]反 = [11111111]补
计算机可以有三种编码方式表示一个数. 对于正数因为三种编码方式的结果都相同:
[+1] = [00000001]原 = [00000001]反 = [00000001]补
所以不需要过多解释. 但是对于负数:
[-1] = [10000001]原 = [11111110]反 = [11111111]补
可见原码, 反码和补码是完全不同的. 为何还会有反码和补码呢?
首先, 因为人脑可以知道第一位是符号位, 在计算的时候我们会根据符号位, 选择对真值区域的加减. (真值的概念在本文最开头).
但是对于计算机, 加减乘数已经是最基础的运算, 要设计的尽量简单. 计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法.
根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法, 这样计算机运算的设计就更简单了.
于是人们开始探索 将符号位参与运算, 并且只保留加法的方法. 首先来看原码:
计算十进制的表达式: 1-1=0
为了解决原码做减法的问题, 出现了反码:
1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0
发现用反码计算减法, 结果的真值部分是正确的. 而唯一的问题其实就出现在"0"这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的. 而且会有[0000 0000]原和[1000 0000]原两个编码表示0.
于是补码的出现, 解决了0的符号以及两个编码的问题:
1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原
这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:
(-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补
-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补 就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的)
使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127].
因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是: [-231, 231-1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.
计算机巧妙地把符号位参与运算, 并且将减法变成了加法, 背后蕴含了怎样的数学原理呢?
将钟表想象成是一个1位的12进制数. 如果当前时间是6点, 我希望将时间设置成4点, 需要怎么做呢?我们可以:
1. 往回拨2个小时: 6 - 2 = 4
2. 往前拨10个小时: (6 + 10) mod 12 = 4
3. 往前拨10+12=22个小时: (6+22) mod 12 =4
2,3方法中的mod是指取模操作, 16 mod 12 =4 即用16除以12后的余数是4.
所以钟表往回拨(减法)的结果可以用往前拨(加法)替代!
现在的焦点就落在了如何用一个正数, 来替代一个负数. 上面的例子我们能感觉出来一些端倪, 发现一些规律. 但是数学是严谨的. 不能靠感觉.
首先介绍一个数学中相关的概念: 同余
两个整数a，b，若它们除以整数m所得的余数相等，则称a，b对于模m同余
记作 a ≡ b (mod m)
读作 a 与 b 关于模 m 同余。
举例说明:
4 mod 12 = 4
16 mod 12 = 4
28 mod 12 = 4
所以4, 16, 28关于模 12 同余.
正数进行mod运算是很简单的. 但是负数呢?
下面是关于mod运算的数学定义:
上面是截图, "取下界"符号找不到如何输入(word中粘贴过来后乱码). 下面是使用"L"和"J"替换上图的"取下界"符号:
x mod y = x - y L x / y J
上面公式的意思是:
x mod y等于 x 减去 y 乘上 x与y的商的下界.
以 -3 mod 2 举例:
-3 mod 2
= -3 - 2xL -3/2 J
= -3 - 2xL-1.5J
= -3 - 2x(-2)
= -3 + 4 = 1
所以:
(-2) mod 12 = 12-2=10
(-4) mod 12 = 12-4 = 8
(-5) mod 12 = 12 - 5 = 7
负数的补码等于它的反码加1，即在其反码的最低位加1就为该数的补码，且在计算机中负数以补码形式进行存储。
已知： 1、int型占4字节（32位二进制）char型占1字节（8位二进制）
2、字符在内存中以ASCII形式存储（A的为65，C为67）
3、在内存中低地址存低位，高地址存高位
先规定一个int型负数int i= - 48829；
原码为：1 000 0000 / 0000 0000/1011 1110/1011 1101
反码为：1 111 1111/ 1111 1111/0100 0001/0100 0010
补码为：1 111 1111/ 1111 1111/0100 0001/0100 0011
即可假设该数在内存中的实际存放为：
低地址位，地址值为&i 0100 0011
0100 0001
1111 1111
高地址位，地址值为&i+3 1111 1111
然后用char型指针p1和p2分别指向地址&i和&i+1，并进行输出，分别得到p1输出字母C，p2输出字母A，即说明了&i地址中的内容为0100 0011，&i+1中的内容为0100 0001
即验证了是以补码形式存储，而不是原码或反码！
#include <stdio.h> int main(void) { int i; char *p1; char *p2; i = -48829; //假设负数存储形式为反码，即为： 1111 1111/ 1111 1111/0100 0001/0100 0011 p1 = &i; //假设p1指向 0100 0011 （67） p2 = p1 + 1;//假设p2指向 0100 0001 （65） printf("%c\n", *p1); //输出字符C（67），得证 printf("%c\n", *p2); //输出字符A（65），得证 getchar(); return 0; }
|--浮点数怎么存储在计算机中
浮点型变量是由符号位+阶码位+尾数位组成。
float型数据 二进制为32位，符号位1位，阶码8位，尾数23位
double型数据 二进制为64位，符号位1位，阶码11位，尾数52位
|--单精度32位存储
1bit 8bit 23bit
|--双精度64位存储
1bit 11bit 52bit
浮点数二进制存储形式，是符号位+阶码位+尾数位（针对有符号数）
浮点数没有无符号数(c语言)
|--阶码：
这里阶码采用移码表示，对于float型数据其规定偏置量为127,阶码有正有负，
对于8位二进制，则其表示范围为-128-127，double型规定为1023，其表示范围为-1024-1023
比如对于float型数据，若阶码的真实值为2，则加上127后为129，其阶码表示形式为10000010
|--尾数:
有效数字位，即部分二进制位(小数点后面的二进制位)，
因为规定M的整数部分恒为1(有效数字位从左边不是0的第一位算起)，所以这个1就不进行存储
|--具体步骤：
把浮点数先化为科学计数法表示形式，eg：1.1111011*2^6，然后取阶码（6）的值加上127（对于float）
计算出阶码，尾数是处小数点后的位数（1111011），如果不够23位，则在后面补0至23位。
最后，符号位+阶码位+尾数位就是其内存中二进制的存储形式
1 eg： 2 #include <stdio.h> 3 #include <stdlib.h> 4 int main(int argc, char *argv[]) 5 { 6 int x = 12; 7 char *q = (char *)&x; 8 float a=125.5; 9 char *p=(char *)&a; 10 11 printf("%d\n", *q); 12 13 printf("%d\n",*p); 14 printf("%d\n",*(p+1)); 15 printf("%d\n",*(p+2)); 16 printf("%d\n",*(p+3)); 17 return 0; 18 } 19 20 output： 21 12 22 0 23 0 24 -5 25 66
|--对于float型:
125.5二进制表示为1111101.1，由于规定尾数的整数部分恒为1，
则表示为1.1111011*2^6，阶码为6，加上127为133，则表示为10000101
而对于尾数将整数部分1去掉，为1111011，在其后面补0使其位数达到23位，
则为11110110000000000000000
内存中的表现形式为：
00000000 低地址
00000000
11111011
01000010 高地址
存储形式为： 00 00 fb 42
依次打印为： 0 0 -5 66
解释下-5,内存中是：11111011，因为是有符号变量所以符号位为1是负数，
所以其真值为符号位不变取反加一，变为：10000101化为十进制为-5.
# include <stdio.h> int main() { int a=-5; printf("a=-5: %x\n", a); return 0; }
xyy@xyy-virtual-machine:~/c_learn$ vim d02_fushu.c xyy@xyy-virtual-machine:~/c_learn$ ./a.out a=-5: fffffffb
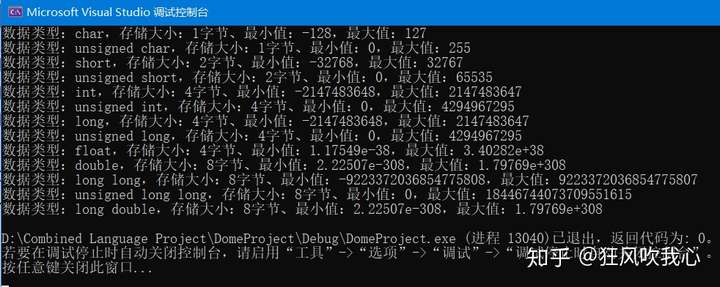
编写C程序时需要考虑每种数据类型在内存中所占的内存大小，即使同一种数据类型在不同平台下所占内存大小亦不相同。为了得到某个类型在特定平台上的准确大写，可以使用sizeof运算符，表达式sizeof(type)得到对象或类型的存储字节大小。
16位系统存储大小2字节，值范围-32768~32767，
32、64位系统存储大小4字节，值范围-2147483648~2147483647；
16位系统存储大小2字节，值范围0~65535，
32、64位系统存储大小4字节，值范围0~4294967295；
16、32位系统存储大小4字节，值范围-2147483648~2147483647，
64位系统存储大小8字节，值范围-9223372036854775808~9223372036854775807；
16、32位系统存储大小4字节，值范围0~4294967295，
64位系统存储大小8字节，值范围0~18446744073709551615；
16位系统存储大小8字节，值范围2.22507*10^-308~1.79769*10^308，
32位系统存储大小12字节（有效位10字节，为了对齐实际分配12字节），值范围3.4*10^-4932 到 1.1*10^4932，
64位系统存储大小16字节（有效位10字节，为了对齐实际分配16字节），值范围3.4*10^-4932 到 1.1*10^4932；
16位系统存储大小2字节，
32位系统存储大小4字节，
64位系统存储大小8字节。
#include <stdio.h> #include <stdlib.h> #include <float.h> int main(void) { printf("数据类型：char，存储大小：%d字节、最小值：%hhd，最大值：%hhd\n", sizeof(char), CHAR_MIN, CHAR_MAX); printf("数据类型：unsigned char，存储大小：%d字节、最小值：%hhu，最大值：%hhu\n", sizeof(unsigned char), 0U, UCHAR_MAX); printf("数据类型：short，存储大小：%d字节、最小值：%hd，最大值：%hd\n", sizeof(short), SHRT_MIN, SHRT_MAX); printf("数据类型：unsigned short，存储大小：%d字节、最小值：%hu，最大值：%hu\n", sizeof(unsigned short), 0U, USHRT_MAX); printf("数据类型：int，存储大小：%d字节、最小值：%d，最大值：%d\n", sizeof(int), INT_MIN, INT_MAX); printf("数据类型：unsigned int，存储大小：%d字节、最小值：%u，最大值：%u\n", sizeof(unsigned int), 0U, UINT_MAX); printf("数据类型：long，存储大小：%d字节、最小值：%ld，最大值：%ld\n", sizeof(long), LONG_MIN, LONG_MAX); printf("数据类型：unsigned long，存储大小：%d字节、最小值：%lu，最大值：%lu\n", sizeof(unsigned long), 0LU, ULONG_MAX); printf("数据类型：float，存储大小：%d字节、最小值：%g，最大值：%g\n", sizeof(float), FLT_MIN, FLT_MAX); printf("数据类型：double，存储大小：%d字节、最小值：%lg，最大值：%lg\n", sizeof(double), DBL_MIN, DBL_MAX); printf("数据类型：long long，存储大小：%d字节、最小值：%lld，最大值：%lld\n", sizeof(long long), LLONG_MIN, LLONG_MAX); printf("数据类型：unsigned long long，存储大小：%d字节、最小值：%llu，最大值：%llu\n", sizeof(unsigned long long), 0LLU, ULLONG_MAX); printf("数据类型：long double，存储大小：%d字节、最小值：%Lg，最大值：%Lg\n", sizeof(long double), LDBL_MIN, LDBL_MAX); return EXIT_SUCCESS; }
运行结果：
char filename[] = "memo.txt"; if ( fopen( filename, "r") == NULL ) perror( filename ); // void表达式
void *malloc( size_t size ); void *realloc( void *ptr, size_t size ); void free( void *ptr );
#include <stdio.h> #include <time.h> #include <stdlib.h> // 提供以下函数的原型 // void srand( unsigned int seed ); // int rand( void ); // void *malloc( size_t size ); // void free( void *ptr ); // void exit( int status }; enum { ARR_LEN = 100 }; int main () { int i, *pNumbers = malloc(ARR_LEN * sizeof(int)); //获得相同的存储空间 if( pNumbers == NULL ) { fprintf(stderr,"Insufficient memory.\n"); exit(1); } srand( (unsigned)time(NULL ); // 初始化随机数产生器 for ( i=0; i < ARR_LEN; ++i ) pNumbers[i] = rand() % 10000; // 存储一些随机数 printf("\n%d random numbers between 0 and 0000:\n", ARR_LEN); for ( i=0; i< ARR_LEN; ++i ) // 循环输出 { printf("%6d",pNumbers[i]); // 每次循环输出一个数字 if ( i % 10 == 9) putchar( ‘\n‘); // 每10个数字换一行 } free( pNumbers ); // 释放存储空间 return 0; }
在此之前需要先明白C语言中的变量和常量都存储在什么地方？
.data段和.bss段：局部变量是存储在栈上的，全局变量存储在.data段和.bss段，其中初始化显示为0的和未赋初值的全局变量存储在.bss段，初始化不为0的存储在.data段，静态局部变量和全局变量的存储类是一样的，其中初始化显示为0的和未赋初值的静态局部变量存储在.bss段，初始化不为0的存储在.data段。
.text段即代码段（在Linux中又叫文本段）：程序代码，const修饰的常量也可能存储在.text段（与编译环境有关）。
heap：根据需求判断要不要使用堆，用的时候自己申请，用完之后自己释放。
stack：局部变量存储在栈上，函数调用传参的过程也会用到栈。
1. auto
auto 关键字在C语言中只有一个作用就是修饰局部变量，表示这个变量是自动局部变量，分配在栈上，平时定义的局部变量就是自动局部变量，只是省略了auto。
2. static
static关键字在C语言中有两种用法
第一种就是修饰局部变量：static修饰的局部变量只是改变了存储类，其存储方式和全局变量一样（其中初始化显示为0的和未赋初值的静态局部变量存储在.bss段，初始化不为0的存储在.data段），链接属性为无链接，作用域和普通局部变量一样。
第二种就是修饰全局变量和函数：static修饰全局变量和函数只是改变了他们的链接属性由外链接变为内链接(.C文件内)，全局变量和函数默认的链接属性为外链接（可以跨文件进行链接）。
3. register
这个关键字不常用，register修饰的变量，编译器会尽量将他们分配在寄存器中，（平时分配的一般变量都是在内存中，分配在寄存器中一样的用，但是读写效率会提高很多）。所以register修饰的变量用在那种变量被反复高频率的使用，通过改善这个变量的访问效率可以极大的提升程序的运行效率。
4. extern
extern用来声明全局变量，声明的目的主要是在a.c中定义全局变量而在b.c中使用该变量。
5. volatile
volatile 可变的 易变的 C语言中volatile用来修饰一个变量，表明这个变量可以被编译器之外的东西改变（编译器不可预知的东西，比如硬件自动更改了这个变量的值，一般这个变量是一个寄存器的值，比如在多线程中在别的线程更改了这个变量的值），如果不该加时加了会降低效率。
6. restrict
C99编译器中支持，很多延续C89的编译器是不支持restrict关键字的，gcc支持。
restrict只用来修饰指针，不能修饰普通变量，用restrict修饰的指针指向的区域别的指针不能来修改。
7. typedef
typedef属于存储类关键字，但是实际上和存储类没关系。
8 const
用 const 定义的变量的值是不允许改变的，即不允许给它重新赋值，即使是赋相同的值也不可以。所以说它定义的是只读变量。这也就意味着必须在定义的时候就给它赋初值。
如果定义的时候未初始化，我们知道，对于未初始化的局部变量，程序在执行的时候会自动把一个很小的负数存放进去。这样后面再给它赋初值的话就是“改变它的值”了，即发生语法错误。
用 const 修饰的变量，无论是全局变量还是局部变量，生存周期都是程序运行的整个过程。全局变量的生存周期为程序运行的整个过程这个是理所当然的。而使用 const 修饰过的局部变量就有了静态特性，它的生存周期也是程序运行的整个过程。我们知道全局变量是静态的，静态的生存周期就是程序运行的整个过程。但是用const修饰过的局部变量只是有了静态特性，并没有说它变成了静态变量。
1.指针是const情况
表示一旦得到了某个变量的地址，不能指向其他变量
int *const q=&I; //q是const
这个意思是q不能再指向别人了
*q=26; //OK
q++; //ERROR
2.所指的值是const
表示不能通过这个指针去修改那个变量(并不能使得那个变量成为const)
Const int * p=&I
i=26，i++//i可以变
p=&j //p也可以变
*p=26//不能通过地址进行赋值
Const int a[]={1,2,3,4,5,5}
数组变量表明已经是const的指针了,这里的const表明数组的每个单元都是const int
所以必须通过初始化进行赋值
标签：指针 循环输出 最大 种类型 大小 bit 二进制 linux data-
原文地址：https://www.cnblogs.com/sd-xyy/p/13210711.html
