标签:++ 技术 site 广度优先 路径问题 sem 其他 bool 修改
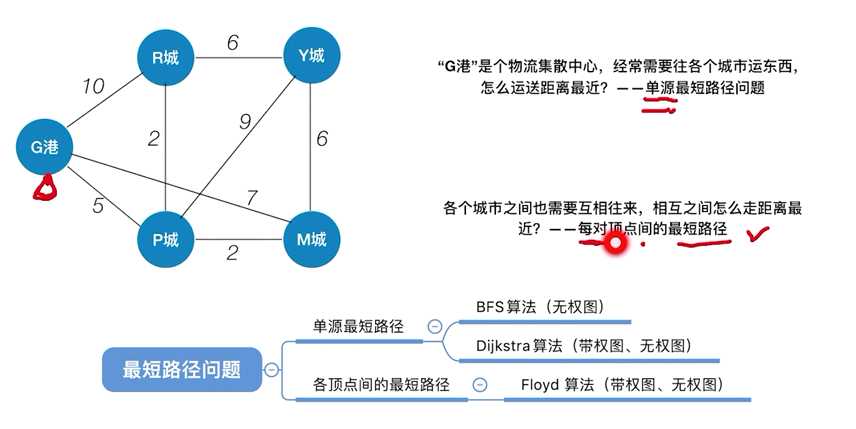
单源最短路径问题
每对顶点间的最短路径
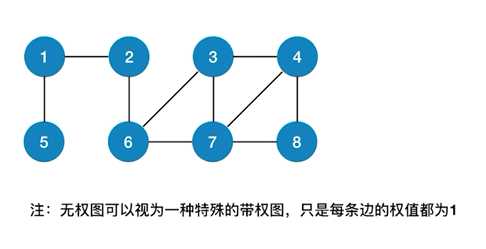

bool visited[MAX_VERTEX_NUM]; //访问标记数组
//广度优先遍历
void BFS(Graph G,int v){ //从定点出发,广度优先遍历图G
visit(v); //访问初始顶点v
visited[v]=TRUE; //对v做已访问标记
Enqueue(Q,v); //顶点v入队列Q
while(!isEmpty(Q)){
DeQueue(Q,v); //顶点v出队列
for(w=FirstNeighbor(G,v);
w>=0;w=NextNeighbor(G,v,w))
//检测v所有邻接点
if(!visited[w]){ //w为v的尚未访问的邻接顶点
visit(w); //访问顶点w
visited[w]=TRUE;//对w做已访问标记
EnQueue(Q,w); //顶点w入队列
}
}
}
//求顶点 u 到其他顶点的最短路径
void BFS_MIN_Distance(Graph G,int u){
//d[i]表示从u到i结点的最短路径
for(i=0;i<G.vexnum;++i){
d[i]=∞; //初始化路径长度
path=[i]=-1;//最短路径从哪个顶点过来
}
d[u]=0;
visited[u]=TRUE; //对v做已访问标记
Enqueue(Q,u); //顶点v入队列Q
while(!isEmpty(Q)){
DeQueue(Q,u); //顶点v出队列
for(w=FirstNeighbor(G,u);
w>=0;w=NextNeighbor(G,u,w))
//检测v所有邻接点
if(!visited[w]){ //w为v的尚未访问的邻接顶点
d[w] = d[u]+1; //路径长度加1
path[w]=u; //最短路径应从u到w
visited[w]=TRUE;//设已访问标记
EnQueue(Q,w); //顶点w入队列
}
}
}
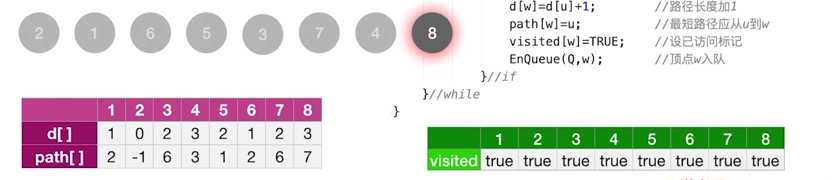
就是对BFS的小修改,在visit一个顶点时,修改最短路径长度d[]并在path[]记录前驱结点

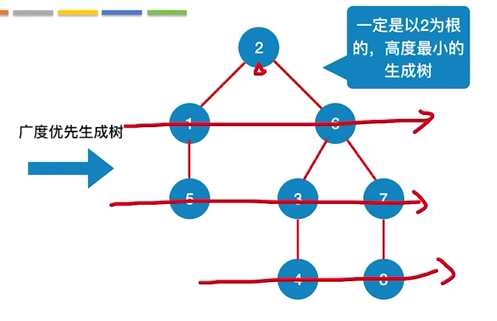
标签:++ 技术 site 广度优先 路径问题 sem 其他 bool 修改
原文地址:https://www.cnblogs.com/jev-0987/p/13213471.html