标签:info mic 练习 lan 顶点 不能 pre src 多个
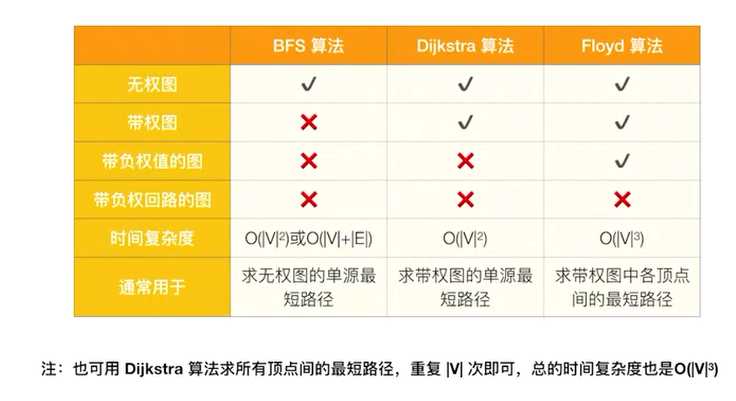
可以用来求带权图和无权图
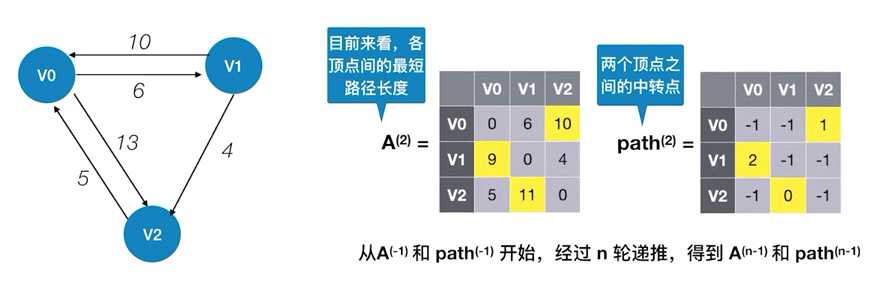
Floyd算法:求出每一对顶点之间的最短路径
使用动态规划思想,将问题的求解分为多个阶段

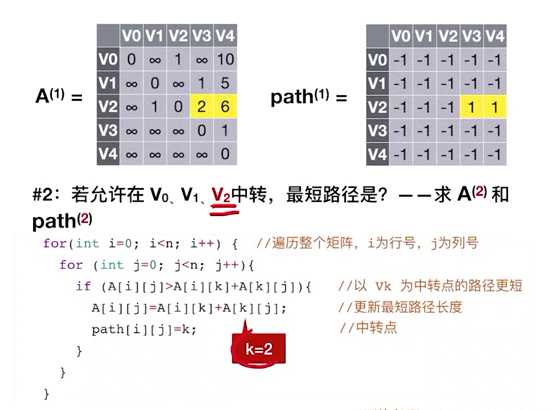
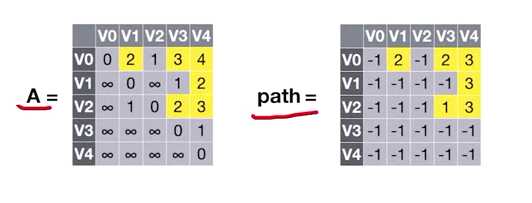
第一个矩阵就是图的邻接矩阵
第二个矩阵表示两个顶点之间的中转点
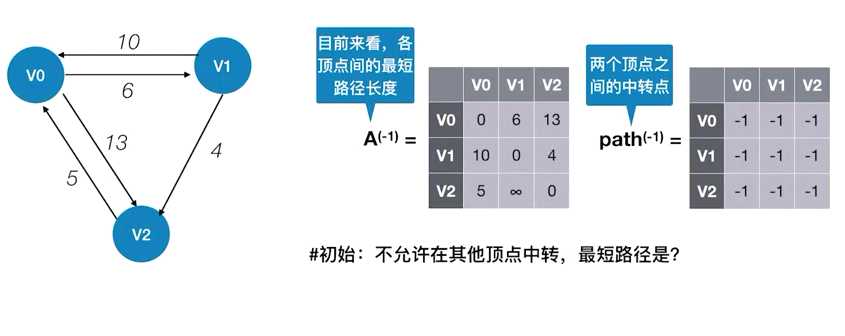
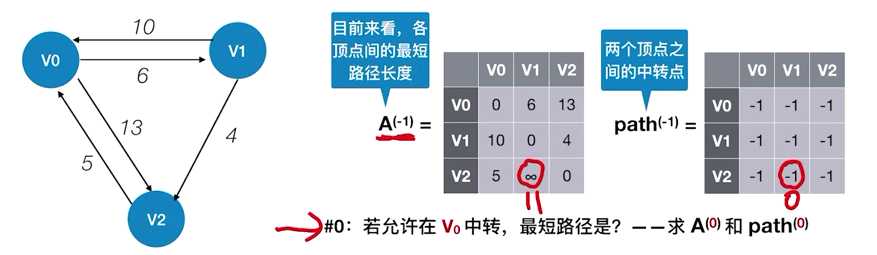
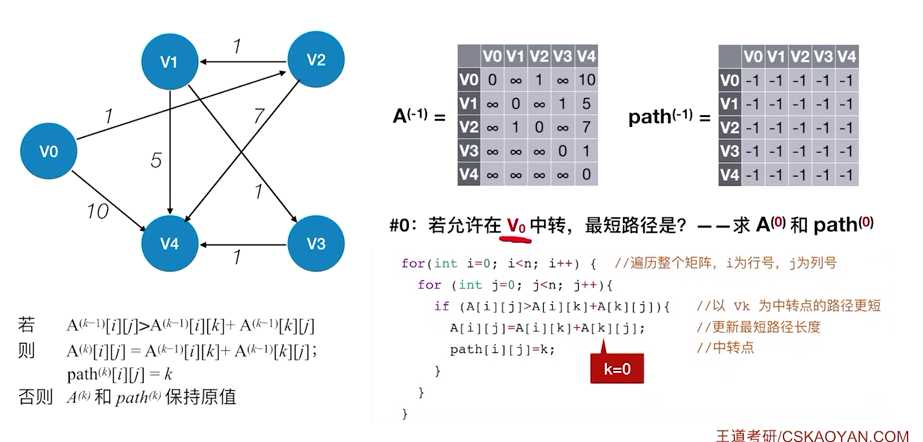
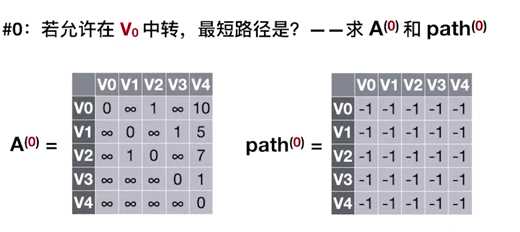
遍历上一个阶段留下来的矩阵A,对于上一个矩阵A当中的每一个具体的元素我们都进行:
若 A^(k-1)[i] [j]>A^(k-1)[i] [k]+A^(k-1)[k] [j]
则 A^(k)[i] [j] = A^(k-1)[i] [k] + A^(k-1)[k] [j];
? path^(k)[i] [j] = k
否则A^(k) 和 path^(k)保持原值
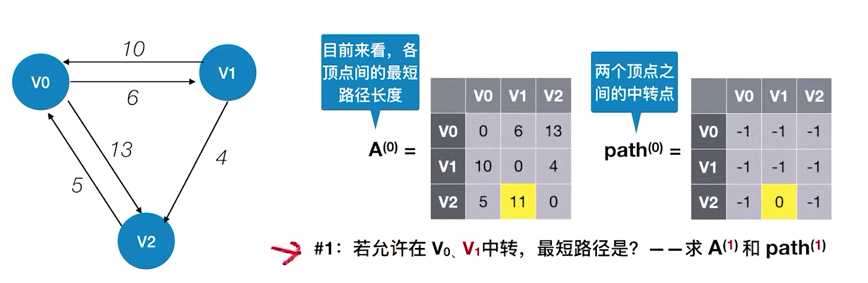
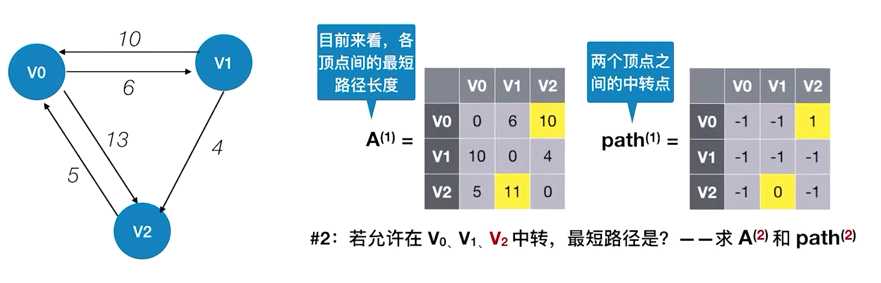


//。。。。准备工作,初始化矩阵A和path
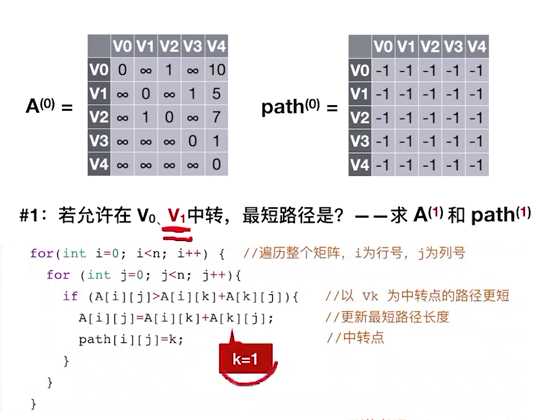
for(int k=0;k<n;k++){ //考虑以vk作为中转点
for(int i=0;i<n;i++){ //遍历整个矩阵,i为行号,j为列号
for(int j=0;j<n;j++){
if(A[i][j]>A[i][k]+A[k][j]){ //以vk作为中转点的路径更短
A[i][j] = A[i][k]+A[k][j]; //更新最短路径长度
path[i][j] = k; //中转点
}
}
}
}








//。。。。准备工作,初始化矩阵A和path
for(int k=0;k<n;k++){ //考虑以vk作为中转点
for(int i=0;i<n;i++){ //遍历整个矩阵,i为行号,j为列号
for(int j=0;j<n;j++){
if(A[i][j]>A[i][k]+A[k][j]){ //以vk作为中转点的路径更短
A[i][j] = A[i][k]+A[k][j]; //更新最短路径长度
path[i][j] = k; //中转点
}
}
}
}
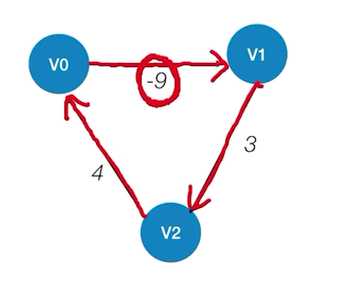
带有“负权值回路”的图
这种图可能没有最短路径
标签:info mic 练习 lan 顶点 不能 pre src 多个
原文地址:https://www.cnblogs.com/jev-0987/p/13213497.html