标签:curd 三角形 操作 oct 包含 style 打开 raw 构造
Koch曲线的构造过程是:取一条长度为L0的直线段,将其三等分,保留两端的线段,将中间的一段改换成夹角为60度的两个等长直线;再将长度为L0/3的4个直线段分别进行三等分,并将它们中间的一段均改换成夹角为60度的两段长为L0/9的直线段;重复以上操作直至无穷,可得以一条具有自相似结构的折线,如图1所示。
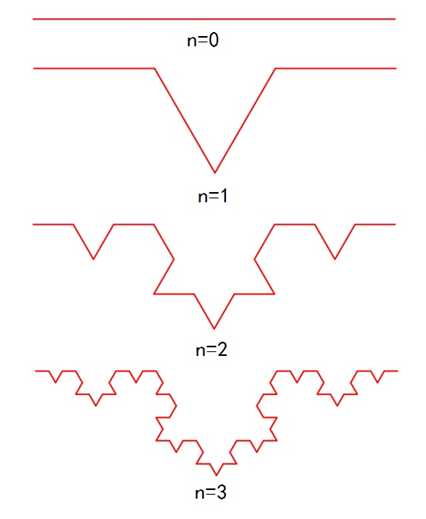
图1 Koch曲线的生成
Koch曲线采用递归过程易于实现,编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>Koch曲线</title>
</head>
<body>
<canvas id="myCanvas" width="600" height="400" style="border:3px double #996633;">
</canvas>
<script type="text/javascript">
var canvas = document.getElementById(‘myCanvas‘);
var ctx = canvas.getContext(‘2d‘);
var maxdepth =5;
var curdepth = 0;
ctx.lineWidth = 2;
Koch({x:50,y:150},{x:550,y:150},Math.PI/3);
function Koch(p1,p2,angle)
{
curdepth++;
if (curdepth<=maxdepth)
{
var x1=(2*p1.x+p2.x)/3;
var y1=(2*p1.y+p2.y)/3;
var x3=(2*p2.x+p1.x)/3;
var y3=(2*p2.y+p1.y)/3;
var x2=(x3-x1)*Math.cos(angle)-(y3-y1)*Math.sin(angle)+x1;
var y2=(x3-x1)*Math.sin(angle)+(y3-y1)*Math.cos(angle)+y1;
Koch(p1,{x:x1,y:y1},Math.PI/3);
Koch({x:x1,y:y1},{x:x2,y:y2},Math.PI/3);
Koch({x:x2,y:y2},{x:x3,y:y3},Math.PI/3);
Koch({x:x3,y:y3},p2,Math.PI/3);
}
if (curdepth>maxdepth)
draw([p1,{x:x1,y:y1},{x:x2,y:y2},{x:x3,y:y3},p2]);
curdepth--;
}
function draw(points)
{
ctx.strokeStyle = "red";
ctx.beginPath()
ctx.moveTo(points[0].x,points[0].y)
for(i=1;i<points.length;i++)
{
ctx.lineTo(points[i].x,points[i].y);
}
ctx.closePath()
ctx.stroke()
}
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出的Koch曲线,如图2所示。

图2 递归深度maxdepth =5的Koch曲线
由图1和2可知,Koch曲线的初始图元是直线,但最终结果却是一条参差不齐的曲线,很像雪花的边缘,如果将3条这样的曲线围在一起,便得到Koch雪花的图案。这样,初始图元不是一条直线,而是一个等边三角形。Koch雪花的生成示例如图3所示。
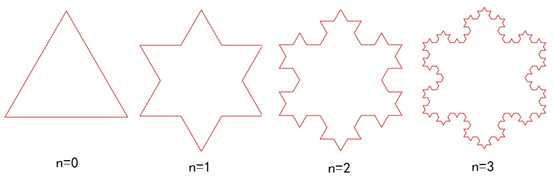
图3 Koch雪花的生成
在程序设计时,定义好等边三角形的三个顶点坐标,调用三次Koch递归过程,以实现等边三角形三条边各自的Koch曲线生成,即可得到Koch雪花图案。编写的HTML文件如下。
<!DOCTYPE html>
<head>
<title>Koch雪花</title>
</head>
<body>
<canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;">
</canvas>
<script type="text/javascript">
var canvas = document.getElementById(‘myCanvas‘);
var ctx = canvas.getContext(‘2d‘);
var maxdepth =5;
var curdepth = 0;
ctx.lineWidth = 2;
Koch({x:50,y:450},{x:500,y:450},Math.PI/3);
Koch({x:275,y:450-225*Math.sqrt(3)},{x:50,y:450},Math.PI/3);
Koch({x:500,y:450},{x:275,y:450-225*Math.sqrt(3)},Math.PI/3);
function Koch(p1,p2,angle)
{
curdepth++;
if (curdepth<=maxdepth)
{
var x1=(2*p1.x+p2.x)/3;
var y1=(2*p1.y+p2.y)/3;
var x3=(2*p2.x+p1.x)/3;
var y3=(2*p2.y+p1.y)/3;
var x2=(x3-x1)*Math.cos(angle)-(y3-y1)*Math.sin(angle)+x1;
var y2=(x3-x1)*Math.sin(angle)+(y3-y1)*Math.cos(angle)+y1;
Koch(p1,{x:x1,y:y1},Math.PI/3);
Koch({x:x1,y:y1},{x:x2,y:y2},Math.PI/3);
Koch({x:x2,y:y2},{x:x3,y:y3},Math.PI/3);
Koch({x:x3,y:y3},p2,Math.PI/3);
}
if (curdepth>maxdepth)
draw([p1,{x:x1,y:y1},{x:x2,y:y2},{x:x3,y:y3},p2]);
curdepth--;
}
function draw(points)
{
ctx.strokeStyle = "red";
ctx.beginPath()
ctx.moveTo(points[0].x,points[0].y)
for(i=1;i<points.length;i++)
{
ctx.lineTo(points[i].x,points[i].y);
}
ctx.closePath()
ctx.stroke()
}
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,在浏览器窗口中可能会绘制出如图4所示的Koch雪花图案。

图4 递归深度maxdepth =5的Koch雪花图案
标签:curd 三角形 操作 oct 包含 style 打开 raw 构造
原文地址:https://www.cnblogs.com/cs-whut/p/13226635.html