标签：链表   选择   相关   开始   ati   ima   htable   平衡二叉查找树   水平   

写在前面：今天来学习一下MySQL中的索引机制。

一、何为索引？

说到索引，第一反应就是它能够加快数据查询的效率，可它到底是个什么东西呢？

数据库的索引是一种为了加速数据表中行记录检索的数据结构

索引的本质是 数据结构

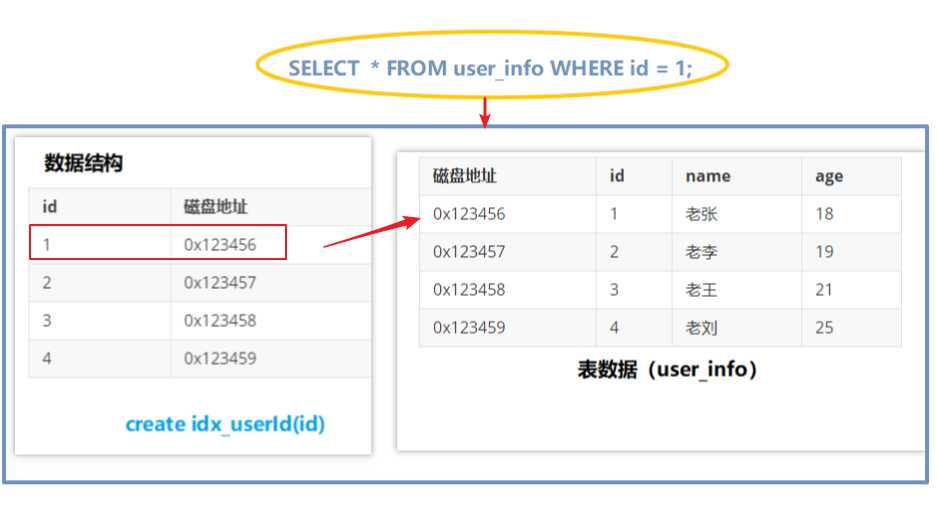
可以看到，我对ID创建了一个索引，形成了数据结构，当我要搜索ID的时候会调用我们的ID索引，直接在数据结构中扫描，找到ID对应的磁盘地址，然后快速定位，返回数据。
当然了这边的这条SQL语句很显然是全表扫描，因为是SELECT *

二、MySQL中的索引机制

我们打开navicat，到建立索引界面，

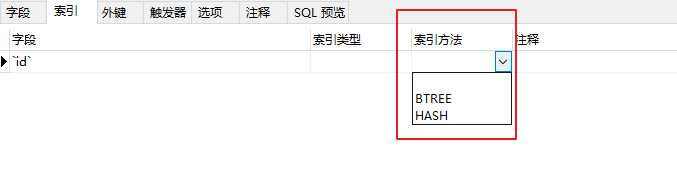
可以看到MySQL存在两种索引机制，Hash和BTREE

Hash索引

以底层数据结构为hashtable的索引结构。
我们在Hash表中进行数据的录入或者删除时,通用步骤:

1. 基于数据的key进行hashcode计算,得到int类型的数值.
2. 基于hash int值与hash表的length进行计算得到下标位置.
3. 基于数组的下标进行数据查找,若查找的下标位存在元素,再判断该存储元素的数据结构.
4. 如果存储元素是链表结构则顺序递归比对.
5. 如果存储元素是红黑树则递归二分查找.
6. 索引的底层数据结构为Hash表结构的话,我们在等值的匹配过程中只需要进行基于数组的下标查找。时间复杂度为O(1)。但是我们也发现在存储元素进行hashcode计算之后,原本可比较大小的多个元素可能得到的hash int值确并不满足原本比较需求.

索引表索引的特点：

• 关键字等值匹配效率高

• 不支持数据的范围查找

B-Tree

要讲B-Tree,就得先讲讲二叉树了

2.2.1二叉树

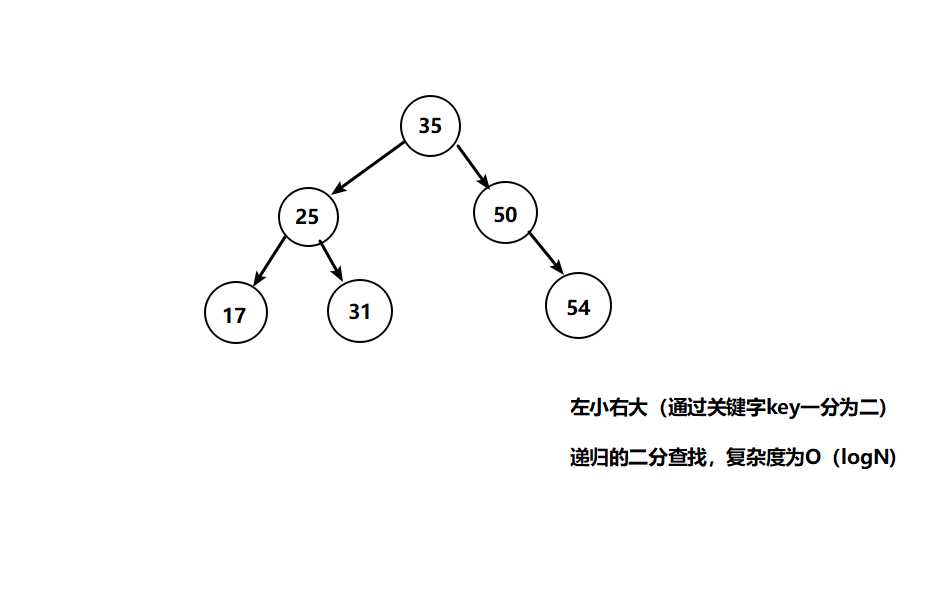
二叉树的每个节点都存储了关键字和数据，每一次查找都是从根节点开始，向下进行递归查找。但是我们发现二叉查找树结构存在数据的倾斜(不规则)性，同时由于其复杂度为O（logN),很显然在大量数据的查找时会耗费很多时间，所以便要对二叉树进行改进，于是有了平衡二叉树。

试想一下，若我针对表中ID字段建立了自增序列，然后选用二叉树作为索引的底层数据结构。

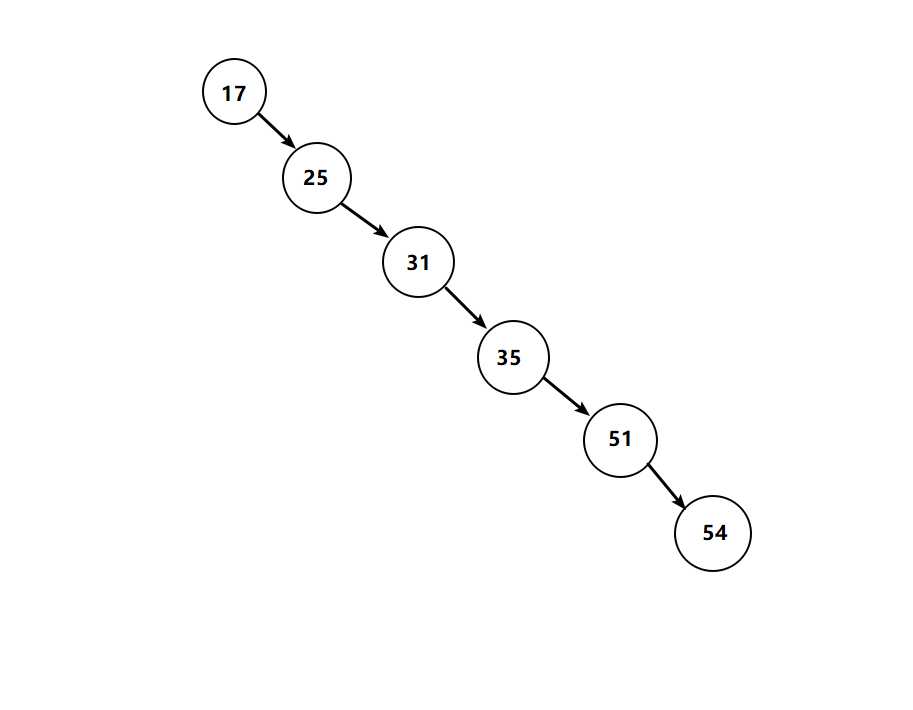
这个时候针对ID的二叉树结构将变为线性链表结构，如果我们再去查找的话就相当于全表扫描，效率很低。究其原因就是因为二叉树的高度太高了，导致查找效率不稳定。

2.2.2平衡二叉树（AVL）

这里推荐一个网页，点击此链接跳转，在其中选择比如B+Tree,然后自己添加节点，可以直观看到这棵树是怎样构成的。

AVL树是最先发明的自平衡二叉查找树,在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树.

ALV树维基百科中有这样的描述：

节点的平衡因子是它的左子树的高度减去它的右子树的高度（有时相反）。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的，并需要重新平衡这个树。

也就是说如果这棵树子树的高度差小于等于1的时候是平衡二叉树，如果大于1则不平衡，需要通过旋转操作对这棵树进行平衡。

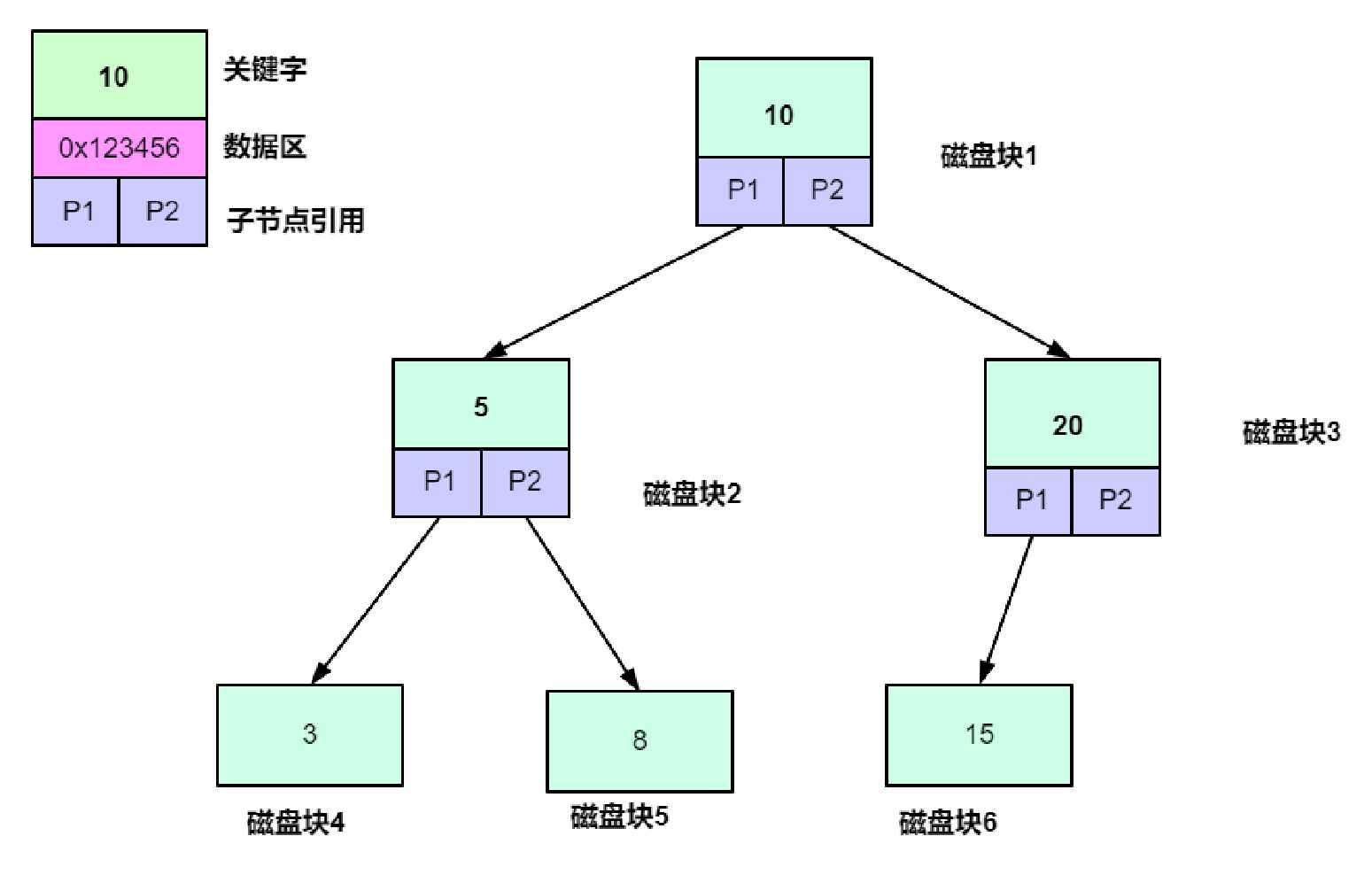
虽然平衡二叉树解决了二叉树查询不稳定的问题，但是平衡二叉树仍然存在一些问题
比如：

• AVL的树高问题.

  在树形结构中,数据的所处树的位置将带来I/O的加载次数.如上图,如果我们需要在图中查找8的数据,我们需要进行磁盘块1[10],磁盘块2[5],磁盘块5[8]的三次加载才能找到数据.AVL虽然能保证平衡,但是由于是二叉树结构必然在大数据量的情况下树高将会很高.

• 磁盘IO的利用率问题.

  在RDBMS系统中,索引都是存储在磁盘中的.操作系统与磁盘的交互是采用页为基本的交换单位.一页数据大小是4KB,再加上操作系统的预读能力[空间局部性原理],一次磁盘的IO交互将会带来N页的数据返回.但是在上图中,我们不难发现,一个磁盘块能承载的数据内容只有一个关键字,一个数据区内容,两个子节点的指针.肯定填充不满4KB或是8KB,16KB的空间.一次低性能的磁盘IO.确只能带会仅仅少量的有效数据.

2.2.3多路平衡查找树（B-Tree）

B-树又叫多路平衡查找树,是一种绝对平衡的树形结构.它的绝对平衡指的是所有的叶子节点数据都同一个水平线上.

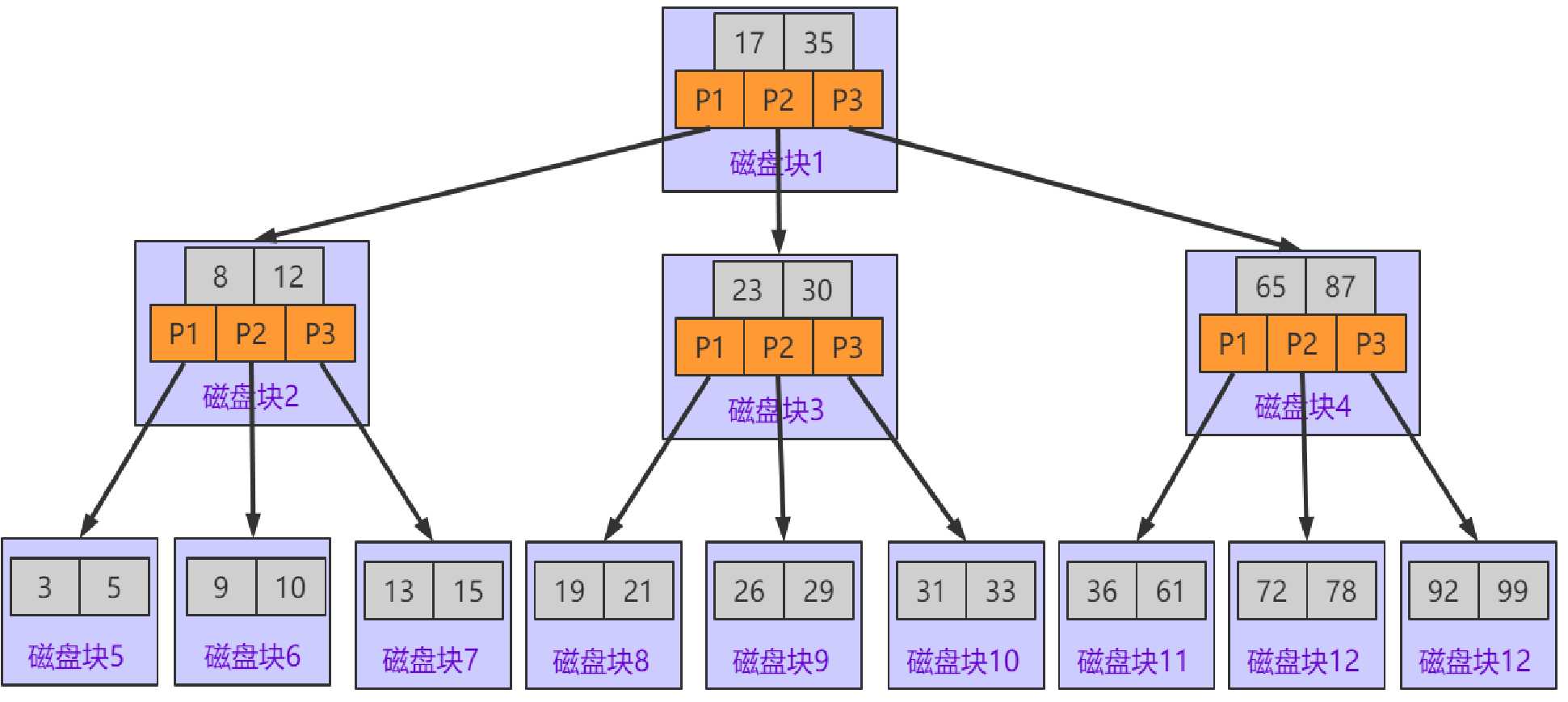
同样我们可以通过之前的网站进行模拟，通过模拟我们发现,数据在进行插入或是删除的
过程中会基于节点个数的变化进行节点的合并和分裂.以达到树的绝对平衡.

总结：B-树的优势

• 将磁盘IO的低效操作通过内存中数据比较进行替换.

  在二叉树中,一次只能加载一个关键字进行匹配.但是在B-树,一次可以加载N个关键字,若将磁盘块(节点)的空间大小固定(MySQL中定义为16KB).磁盘块能存储的关键字个数就会与单个关键字内容占用的空间相关.基于预读和操作系统磁盘交互特性.磁盘I/O一次加载的内容正好都是需要比对的内容.将内容的多次I/O加载转换成在内存中进行数据的比较.

• 合理的降低树的高度,减少IO的次数.
  在树形结构中数据的所处高度位置,将带来IO的次数不一样.B-Tree结构合理的降低了树的高度.也就意味着数据的I/O次数将降低基于以上的特点,所以很多关系型数据库都采用B-Tree,或是B-Tree的变种数据结构作为索引的底层数据结构.

2.3加强版的多路平衡查找树（B+Tree）

• B+树是基于B-树结构的加强版树形结构.
• B-树拥有的特性B+树都拥有.
• B+树的数据匹对规则采用闭合区间的方式
• B+树的非叶子节点上不保存关键字对应的数据区
• B+树的叶子节点上保存数据区
• 在叶子节点上的数据产生形成首尾相连的链式结构带来更高效的数据排序

总结

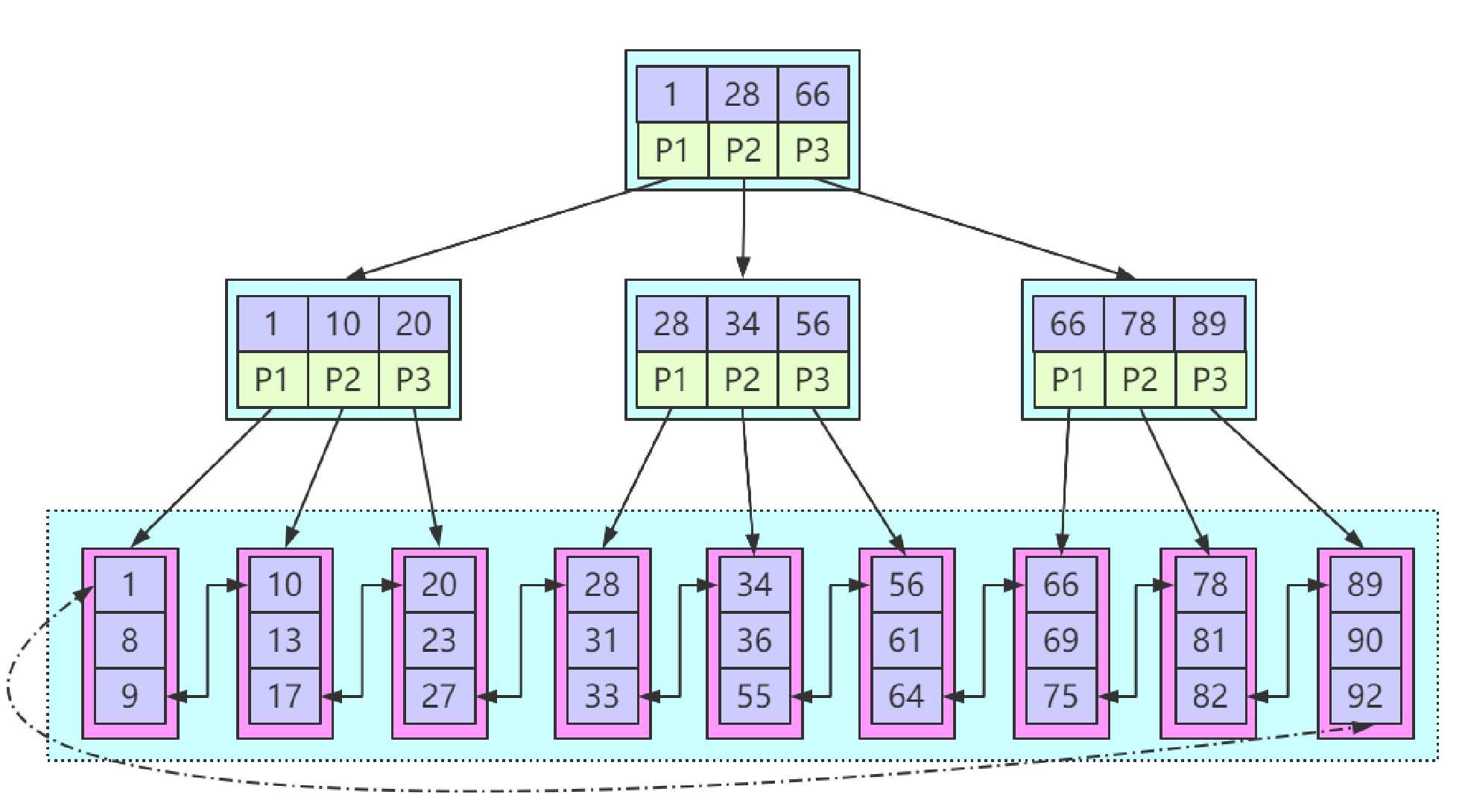
B+Tree相较于B-Tree的优势：

• B-树拥有的特性,B+树都拥有.
• B+树拥有更强劲的磁盘IO能力.在非叶子节点不存在数据区,将大大降低节点的空间占用.能存储
  更多的关键字.一次磁盘IO带回来的有效数据将更多更精准.
• B+树拥有更好的数据排序能力
  这是B+树的天然优势,在最末尾的叶子节点这一层天然即有序的链式结构.
• 基于B+树的扫表能力更强
  在B+树的数据结构中,若需要扫表,只需要扫描最末尾的叶子节点即可.
• 基于B+树结构的索引的查询,更趋于稳定
  在B-树结构中,我们发现,我们的关键字在某一个节点进行匹对成功就完成数据区内容的返回.但是在B+树结构中,我们采用的是闭合区间的比对方式即数据的最终加载一定会在叶子节点上.在B-树结构中,有可能针对一张表的查询,有些数据需要3次IO.有些只需要1次IO.前后的查询效率跌跌宕宕不稳定.但是在B+树结构中一定恒定的IO次数,带来更稳定的查询效率.

PS:本博文仅作为学习交流使用。

MySQL B+Tree索引机制

标签：链表   选择   相关   开始   ati   ima   htable   平衡二叉查找树   水平   

原文地址：https://www.cnblogs.com/jshmztl/p/13204405.html