标签:external specific overview actor ble disco env second aaaaa
Java programmers use data structures to store and organize data, and we use algorithms to manipulate the data in those structures. The more you understand about data structures and algorithms, and how they work together, the more efficient your Java programs will be.
This tutorial launches a short series introducing data structures and algorithms. In Part 1, you‘ll learn what a data structure is and how data structures are classified. You‘ll also learn what an algorithm is, how algorithms are represented, and how to use time and space complexity functions to compare similar algorithms. Once you‘ve got these basics, you‘ll be ready to learn about searching and sorting with one-dimensional arrays, in Part 2.
Data structures are based on abstract data types (ADT), which Wikipedia defines as follows:
[A] mathematical model for data types where a data type is defined by its behavior (semantics) from the point of view of a user of the data, specifically in terms of possible values, possible operations on data of this type, and the behavior of these operations.
An ADT doesn‘t care about the memory representation of its values or how its operations are implemented. It‘s like a Java interface, which is a data type that‘s disconnected from any implementation. In contrast, a data structure is a concrete implementation of one or more ADTs, similar to how Java classes implement interfaces.
Examples of ADTs include Employee, Vehicle, Array, and List. Consider the List ADT (also known as the Sequence ADT), which describes an ordered collection of elements that share a common type. Each element in this collection has its own position and duplicate elements are allowed. Basic operations supported by the List ADT include:
Data structures that can implement the List ADT include fixed-size and dynamically sized one-dimensional arrays and singly-linked lists. (You‘ll be introduced to arrays in Part 2, and linked lists in Part 3.)
There are many kinds of data structures, ranging from single variables to arrays or linked lists of objects containing multiple fields. All data structures can be classified as primitives or aggregates, and some are classified as containers.
The simplest kind of data structure stores single data items; for example, a variable that stores a Boolean value or a variable that stores an integer. I refer to such data structures as primitives.
Many data structures are capable of storing multiple data items. For example, an array can store multiple data items in its various slots, and an object can store multiple data items via its fields. I refer to these data structures as aggregates.
All of the data structures we‘ll look at in this series are aggregates.
Anything from which data items are stored and retrieved could be considered a data structure. Examples include the data structures derived from the previously mentioned Employee, Vehicle, Array, and List ADTs.
Many data structures are designed to describe various entities. Instances of an Employee class are data structures that exist to describe various employees, for instance. In contrast, some data structures exist as generic storage vessels for other data structures. For example, an array can store primitive values or object references. I refer to this latter category of data structures as containers.
As well as being aggregates, all of the data structures we‘ll look at in this series are containers.
The Java Collections Framework supports many kinds of container-oriented data structures and associated algorithms. This series will help you better understand this framework.
It‘s become fairly common to use design patterns to introduce university students to data structures. A Brown University paper surveys several design patterns that are useful for designing high-quality data structures. Among other things, the paper demonstrates that the Adapter pattern is useful for designing stacks and queues. The demonstration code is shown in Listing 1.
public class DequeStack implements Stack
{
Deque D; // holds the elements of the stack
public DequeStack()
{
D = new MyDeque();
}
@Override
public int size()
{
return D.size();
}
@Override
public boolean isEmpty()
{
return D.isEmpty();
}
@Override
public void push(Object obj)
{
D.insertLast(obj);
}
@Override
public Object top() throws StackEmptyException
{
try
{
return D.lastElement();
}
catch(DequeEmptyException err)
{
throw new StackEmptyException();
}
}
@Override
public Object pop() throws StackEmptyException
{
try
{
return D.removeLast();
}
catch(DequeEmptyException err)
{
throw new StackEmptyException();
}
}
}Listing 1 excerpts the Brown University paper‘s DequeStack class, which demonstrates the Adapter pattern. Note that Stack and Deque are interfaces that describe Stack and Deque ADTs. MyDeque is a class that implements Deque.
The original code that Listing 1 is based on didn‘t present the source code to Stack, Deque, and MyDeque. For clarity, I‘ve introduced @Override annotations to show that all of DequeStack‘s non-constructor methods override Stack methods.
DequeStack adapts MyDeque so that it can implement Stack. All of DequeStack‘s method are one-line calls to the Deque interface‘s methods. However, there is a small wrinkle in which Deque exceptions are converted into Stack exceptions.
Historically used as a tool for mathematical computation, algorithms are deeply connected with computer science, and with data structures in particular. An algorithm is a sequence of instructions that accomplishes a task in a finite period of time. Qualities of an algorithm are as follows:
Note that while programs may be algorithmic in nature, many programs do not terminate without external intervention.
Many code sequences qualify as algorithms. One example is a code sequence that prints a report. More famously, Euclid‘s algorithm is used to calculate the mathematical greatest common divisor. A case could even be made that a data structure‘s basic operations (such as store value in array slot) are algorithms. In this series, for the most part, I‘ll focus on higher-level algorithms used to process data structures, such as the Binary Search and Matrix Multiplication algorithms.
How do you represent an algorithm? Writing code before fully understanding its underlying algorithm can lead to bugs, so what‘s a better alternative? Two options are flowcharts and pseudocode.
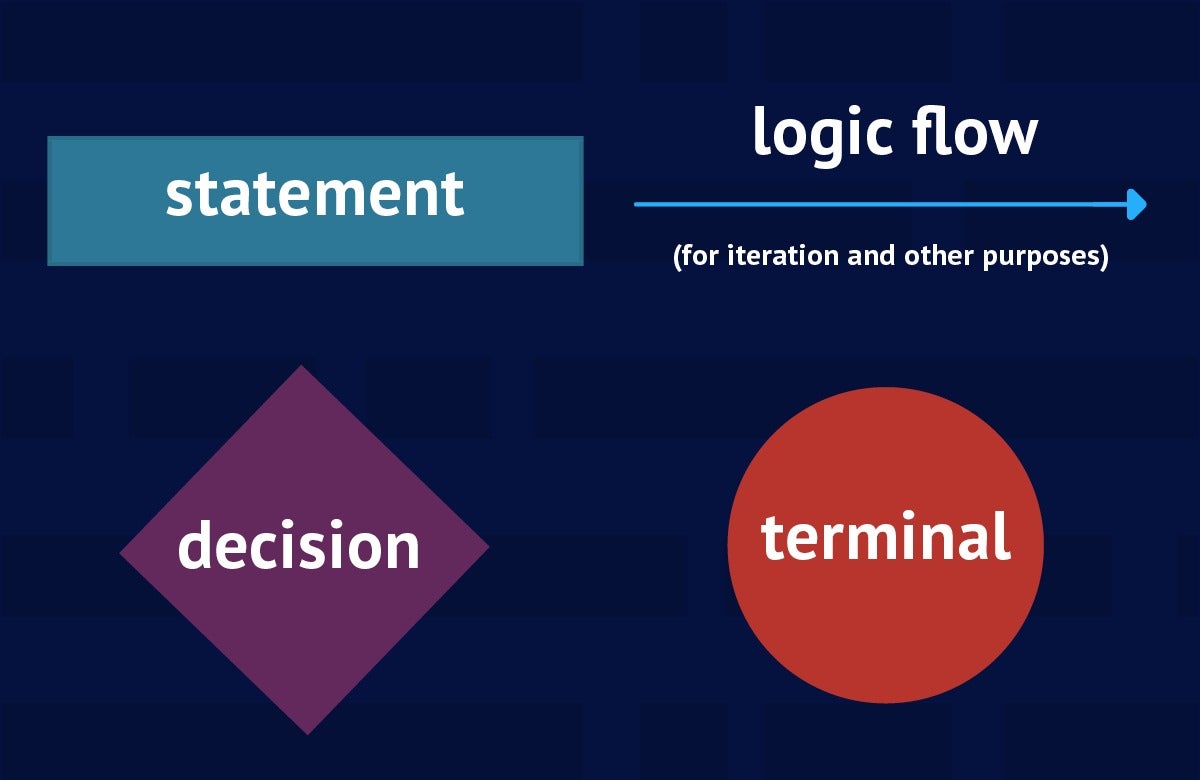
A flowchart is a visual representation of an algorithm‘s control flow. This representation illustrates statements that need to be executed, decisions that need to be made, logic flow (for iteration and other purposes), and terminals that indicate start and end points. Figure 1 reveals the various symbols that flowcharts use to visualize algorithms.
 IDG
IDG
Figure 1. Flowcharts use symbols to represent statements, decisions, logic flow, and terminals
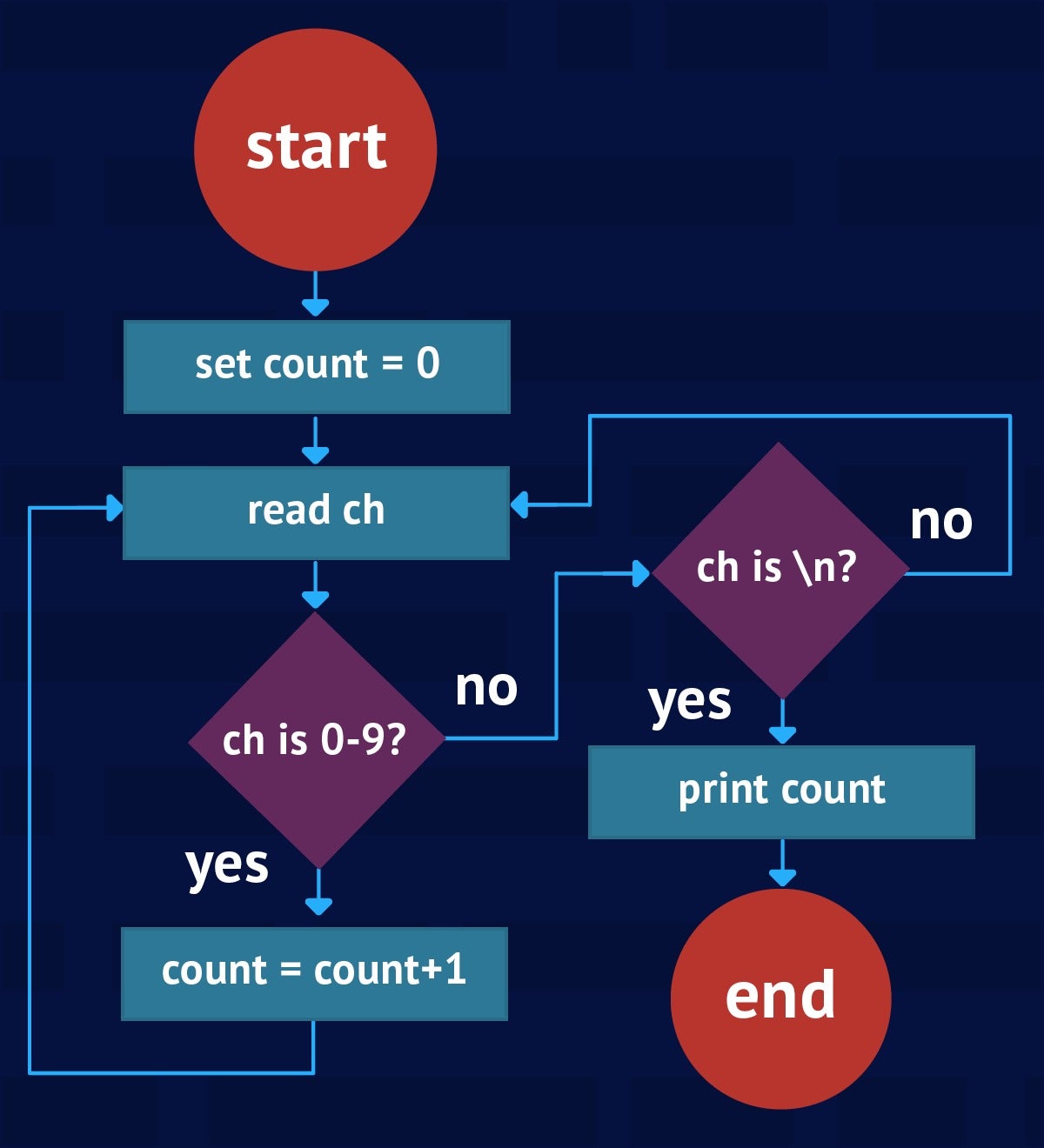
Consider an algorithm that initializes a counter to 0, reads characters until a newline (\n) character is seen, increments the counter for each digit character that‘s been read, and prints the counter‘s value after the newline character has been read. The flowchart in Figure 2 illustrates this algorithm‘s control flow.
 IDG
IDG
Figure 2. This flowchart shows how to count from 0 to 9
A flowchart‘s simplicity and its ability to present an algorithm‘s control flow visually (so that it‘s is easy to follow) are its major advantages. Flowcharts also have several disadvantages, however:
An alternative to flowcharts is pseudocode, which is a textual representation of an algorithm that approximates the final source code. Pseudocode is useful for quickly writing down an algorithm‘s representation. Because syntax is not a concern, there are no hard-and-fast rules for writing pseudocode.
You should strive for consistency when writing pseudocode. Being consistent will make it much easier to translate the pseudocode into actual source code. For example, consider the following pseudocode representation of the previous counter-oriented flowchart:
DECLARE CHARACTER ch = ‘‘
DECLARE INTEGER count = 0
DO
READ ch
IF ch GE ‘0‘ AND ch LE ‘9‘ THEN
count = count + 1
END IF
UNTIL ch EQ ‘\n‘
PRINT count
ENDThe pseudocode first presents a couple of DECLARE statements that introduce variables ch and count, initialized to default values. It then presents a DO loop that executes UNTIL ch contains \n (the newline character), at which point the loop ends and a PRINT statement outputs count‘s value.
For each loop iteration, READ causes a character to be read from the keyboard (or perhaps a file--in this case it doesn‘t matter what constitutes the underlying input source) and assigned to ch. If this character is a digit (one of 0 through 9), count is incremented by 1.
The data structures and algorithms you use critically affect two factors in your applications:
It follows that you should be especially mindful of the algorithms and data structures you use for applications that will process lots of data. These include applications used for big data and the Internet of Things.
When choosing a data structure or algorithm, you will sometimes discover an inverse relationship between memory usage and CPU time: the less memory a data structure uses, the more CPU time associated algorithms need to process the data structure‘s data items. Also, the more memory a data structure uses, the less CPU time associated algorithms will need to process the data items–leading to faster algorithm results.
As much as possible, you should strive to balance memory use with CPU time. You can simplify this task by analyzing algorithms to determine their efficiency. How well does one algorithm perform against another of similar nature? Answering this question will help you make good choices given a choice between multiple algorithms.
Some algorithms perform better than others. For example, the Binary Search algorithm is almost always more efficient than the Linear Search algorithm–something you‘ll see for yourself in Part 2. You want to choose the most efficient algorithm for your application‘s needs, but that choice might not be as obvious as you would think.
For instance, what does it mean if the Selection Sort algorithm (introduced in Part 2) takes 0.4 seconds to sort 10,000 integers on a given machine? That benchmark is only valid for that particular machine, that particular implementation of the algorithm, and for the size of the input data.
As computer scientist, we use time complexity and space complexity to measure an algorithm‘s efficiency, distilling these into complexity functions to abstract implementation and runtime environment details. Complexity functions reveal the variance in an algorithm‘s time and space requirements based on the amount of input data:
Both complexity functions are based on the size of input (n), which somehow reflects the amount of input data. Consider the following pseudocode for array printing:
DECLARE INTEGER i, x[] = [ 10, 15, -1, 32 ]
FOR i = 0 TO LENGTH(x) - 1
PRINT x[i]
NEXT i
ENDYou can express the time complexity of this algorithm by specifying the time-complexity function t(n) = an+b, where a (a constant multiplier) represents the amount of time to complete one loop iteration, and b represents the algorithm‘s setup time. In this example, the time complexity is linear.
Data structures and algorithms in Java, Part 1: Overview
标签:external specific overview actor ble disco env second aaaaa
原文地址:https://www.cnblogs.com/zhijicompanyethan/p/13229533.html