标签：rap svd handler text 必须 笛卡尔 intercept 点击 att
?
在精算科学和保险费率制定中，考虑到风险敞口可能是一场噩梦。不知何故，简单的结果是因为计算起来更加复杂，只是因为我们必须考虑到暴露是一个异构变量这一事实。
保险费率制定中的风险敞口可以看作是审查数据的问题（在我的数据集中，风险敞口始终小于1，因为观察结果是合同，而不是保单持有人），利息变量是未观察到的变量，因为我们必须为保险合同定价一年（整年）的保险期。因此，我们必须对保险索赔的年度频率进行建模。
?
在我们的数据集中，我们考虑索赔总数与总风险承担比率。例如，如果我们考虑泊松过程，可能性是
?
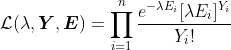
即
?
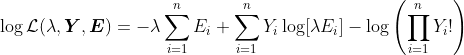
因此，我们有一个预期值的估算，一个自然估算 。
现在，我们需要估算方差，更准确地说是条件变量。
这可以用来检验泊松假设是否对频率建模有效。考虑以下数据集，
> nombre=rbind(nombre1,nombre2)
> baseFREQ = merge(contrat,nombre)在这里，我们确实有两个感兴趣的变量，即每张合约的敞口，
> E <- baseFREQ$exposition和（观察到的）索赔数量（在该时间段内）
> Y <- baseFREQ$nbre无需协变量，可以计算每个合同的平均（每年）索赔数量以及相关的方差
> (mean=weighted.mean(Y/E,E))
[1] 0.07279295
> (variance=sum((Y-mean*E)^2)/sum(E))
[1] 0.08778567看起来方差（略）大于平均值（我们将在几周后看到如何更正式地对其进行测试）。可以在保单持有人居住的地区添加协变量，例如人口密度，
Density, zone 11 average = 0.07962411 variance = 0.08711477
Density, zone 21 average = 0.05294927 variance = 0.07378567
Density, zone 22 average = 0.09330982 variance = 0.09582698
Density, zone 23 average = 0.06918033 variance = 0.07641805
Density, zone 24 average = 0.06004009 variance = 0.06293811
Density, zone 25 average = 0.06577788 variance = 0.06726093
Density, zone 26 average = 0.0688496 variance = 0.07126078
Density, zone 31 average = 0.07725273 variance = 0.09067
Density, zone 41 average = 0.03649222 variance = 0.03914317
Density, zone 42 average = 0.08333333 variance = 0.1004027
Density, zone 43 average = 0.07304602 variance = 0.07209618
Density, zone 52 average = 0.06893741 variance = 0.07178091
Density, zone 53 average = 0.07725661 variance = 0.07811935
Density, zone 54 average = 0.07816105 variance = 0.08947993
Density, zone 72 average = 0.08579731 variance = 0.09693305
Density, zone 73 average = 0.04943033 variance = 0.04835521
Density, zone 74 average = 0.1188611 variance = 0.1221675
Density, zone 82 average = 0.09345635 variance = 0.09917425
Density, zone 83 average = 0.04299708 variance = 0.05259835
Density, zone 91 average = 0.07468126 variance = 0.3045718
Density, zone 93 average = 0.08197912 variance = 0.09350102
Density, zone 94 average = 0.03140971 variance = 0.04672329可以可视化该信息
> plot(meani,variancei,cex=sqrt(Ei),col="grey",pch=19,
+ xlab="Empirical average",ylab="Empirical variance")
> points(meani,variancei,cex=sqrt(Ei))
?
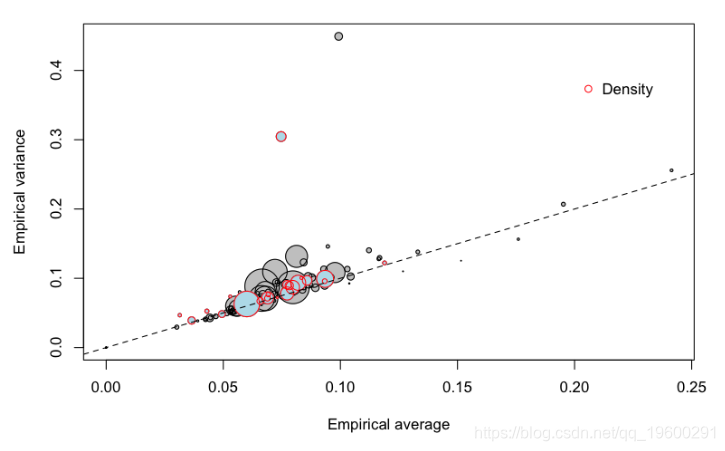
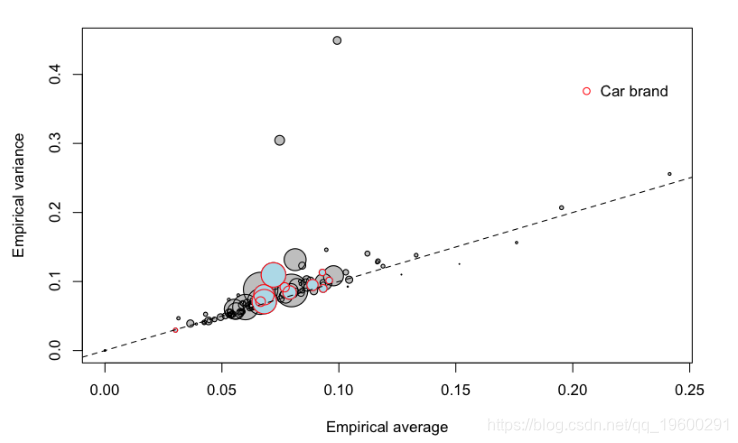
圆圈的大小与组的大小有关（面积与组内的总暴露量成正比）。第一个对角线对应于泊松模型，即方差应等于均值。也可以考虑其他协变量
?
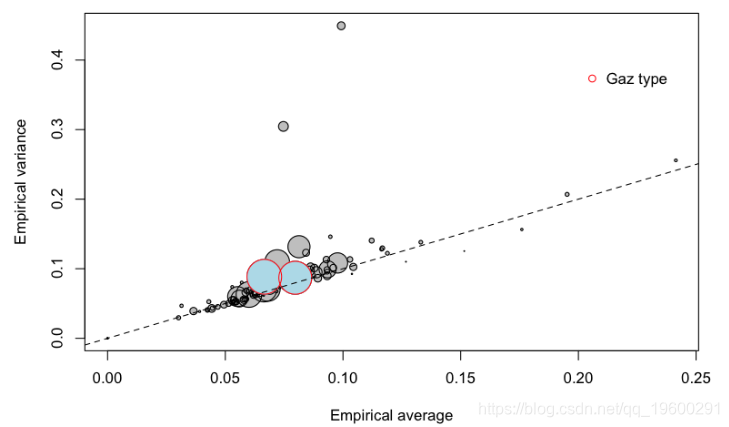
或汽车品牌，
?
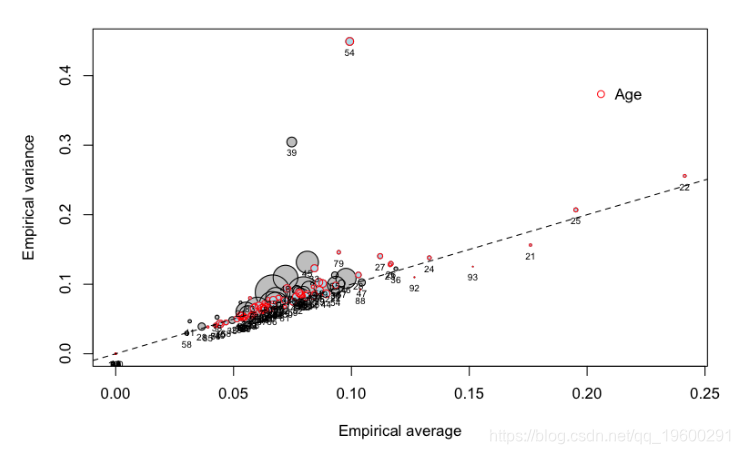
也可以将驾驶员的年龄视为分类变量
?
让我们更仔细地看一下不同年龄段的人，
?
在右边，我们可以观察到年轻的（没有经验的）驾驶员。那是预料之中的。但是有些类别 低于 第一个对角线：期望的频率很大，但方差不大。也就是说，我们 可以肯定的 是，年轻的驾驶员会发生更多的车祸。相反，它不是一个异类：年轻的驾驶员可以看作是一个相对同质的类，发生车祸的频率很高。
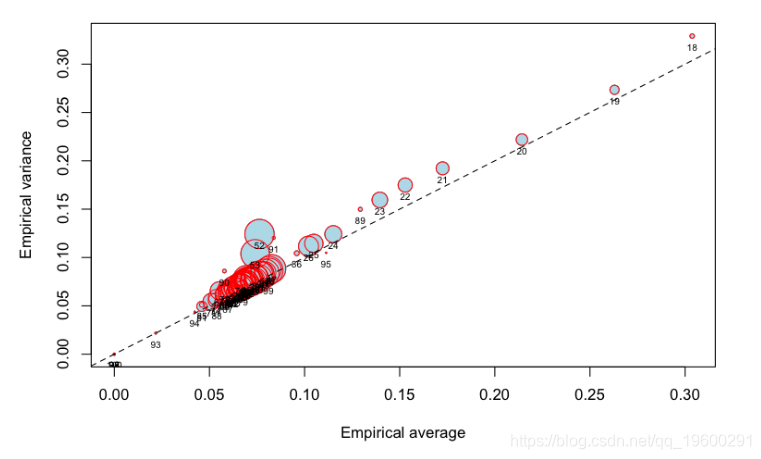
使用原始数据集（在这里，我仅使用具有50,000个客户的子集），我们确实获得了以下图形：
?
由于圈正在从18岁下降到25岁，因此具有明显的经验影响。
同时我们可以发现有可能将曝光量视为标准变量，并查看系数实际上是否等于1。如果没有任何协变量，
Call:
glm(formula = Y ~ log(E), family = poisson("log"))
Deviance Residuals:
Min 1Q Median 3Q Max
-0.3988 -0.3388 -0.2786 -0.1981 12.9036
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.83045 0.02822 -100.31 <2e-16 ***
log(E) 0.53950 0.02905 18.57 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 12931 on 49999 degrees of freedom
Residual deviance: 12475 on 49998 degrees of freedom
AIC: 16150
Number of Fisher Scoring iterations: 6也就是说，该参数显然严格小于1。它与重要性均不相关，
Linear hypothesis test
Hypothesis:
log(E) = 1
Model 1: restricted model
Model 2: Y ~ log(E)
Res.Df Df Chisq Pr(>Chisq)
1 49999
2 49998 1 251.19 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1我也没有考虑协变量，
Deviance Residuals:
Min 1Q Median 3Q Max
-0.7114 -0.3200 -0.2637 -0.1896 12.7104
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -14.07321 181.04892 -0.078 0.938042
log(exposition) 0.56781 0.03029 18.744 < 2e-16 ***
carburantE -0.17979 0.04630 -3.883 0.000103 ***
as.factor(ageconducteur)19 12.18354 181.04915 0.067 0.946348
as.factor(ageconducteur)20 12.48752 181.04902 0.069 0.945011因此，假设暴露是此处的外生变量可能是一个过强的假设。
接下来我们开始讨论建模索赔频率时的过度分散。在前面，我讨论了具有不同暴露程度的经验方差的计算。但是我只使用一个因素来计算类。当然，可以使用更多的因素。例如，使用因子的笛卡尔积，
Class D A (17,24] average = 0.06274415 variance = 0.06174966
Class D A (24,40] average = 0.07271905 variance = 0.07675049
Class D A (40,65] average = 0.05432262 variance = 0.06556844
Class D A (65,101] average = 0.03026999 variance = 0.02960885
Class D B (17,24] average = 0.2383109 variance = 0.2442396
Class D B (24,40] average = 0.06662015 variance = 0.07121064
Class D B (40,65] average = 0.05551854 variance = 0.05543831
Class D B (65,101] average = 0.0556386 variance = 0.0540786
Class D C (17,24] average = 0.1524552 variance = 0.1592623
Class D C (24,40] average = 0.0795852 variance = 0.09091435
Class D C (40,65] average = 0.07554481 variance = 0.08263404
Class D C (65,101] average = 0.06936605 variance = 0.06684982
Class D D (17,24] average = 0.1584052 variance = 0.1552583
Class D D (24,40] average = 0.1079038 variance = 0.121747
Class D D (40,65] average = 0.06989518 variance = 0.07780811
Class D D (65,101] average = 0.0470501 variance = 0.04575461
Class D E (17,24] average = 0.2007164 variance = 0.2647663
Class D E (24,40] average = 0.1121569 variance = 0.1172205
Class D E (40,65] average = 0.106563 variance = 0.1068348
Class D E (65,101] average = 0.1572701 variance = 0.2126338
Class D F (17,24] average = 0.2314815 variance = 0.1616788
Class D F (24,40] average = 0.1690485 variance = 0.1443094
Class D F (40,65] average = 0.08496827 variance = 0.07914423
Class D F (65,101] average = 0.1547769 variance = 0.1442915
Class E A (17,24] average = 0.1275345 variance = 0.1171678
Class E A (24,40] average = 0.04523504 variance = 0.04741449
Class E A (40,65] average = 0.05402834 variance = 0.05427582
Class E A (65,101] average = 0.04176129 variance = 0.04539265
Class E B (17,24] average = 0.1114712 variance = 0.1059153
Class E B (24,40] average = 0.04211314 variance = 0.04068724
Class E B (40,65] average = 0.04987117 variance = 0.05096601
Class E B (65,101] average = 0.03123003 variance = 0.03041192
Class E C (17,24] average = 0.1256302 variance = 0.1310862
Class E C (24,40] average = 0.05118006 variance = 0.05122782
Class E C (40,65] average = 0.05394576 variance = 0.05594004
Class E C (65,101] average = 0.04570239 variance = 0.04422991
Class E D (17,24] average = 0.1777142 variance = 0.1917696
Class E D (24,40] average = 0.06293331 variance = 0.06738658
Class E D (40,65] average = 0.08532688 variance = 0.2378571
Class E D (65,101] average = 0.05442916 variance = 0.05724951
Class E E (17,24] average = 0.1826558 variance = 0.2085505
Class E E (24,40] average = 0.07804062 variance = 0.09637156
Class E E (40,65] average = 0.08191469 variance = 0.08791804
Class E E (65,101] average = 0.1017367 variance = 0.1141004
Class E F (17,24] average = 0 variance = 0
Class E F (24,40] average = 0.07731177 variance = 0.07415932
Class E F (40,65] average = 0.1081142 variance = 0.1074324
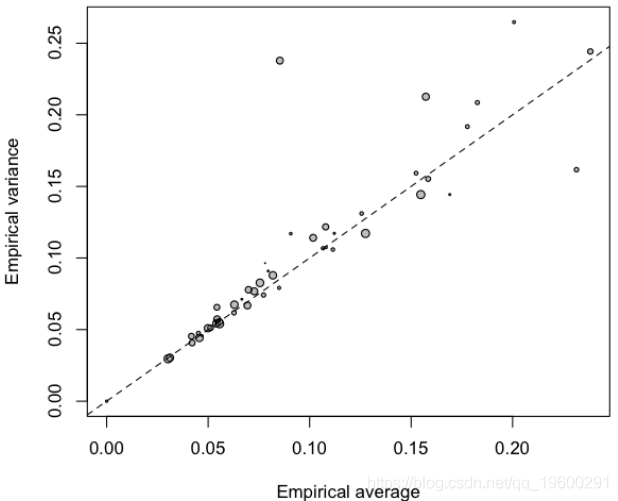
Class E F (65,101] average = 0.09071118 variance = 0.1170159同样，可以将方差与平均值作图，
> plot(vm,vv,cex=sqrt(ve),col="grey",pch=19,
+ xlab="Empirical average",ylab="Empirical variance")
> points(vm,vv,cex=sqrt(ve))
> abline(a=0,b=1,lty=2)
?
一种替代方法是使用树。树可以从其他变量获得，但它应该是相当接近我们理想的模型。在这里，我确实使用了整个数据库（超过60万行）
树如下
> plot(T)
> text(T)
?
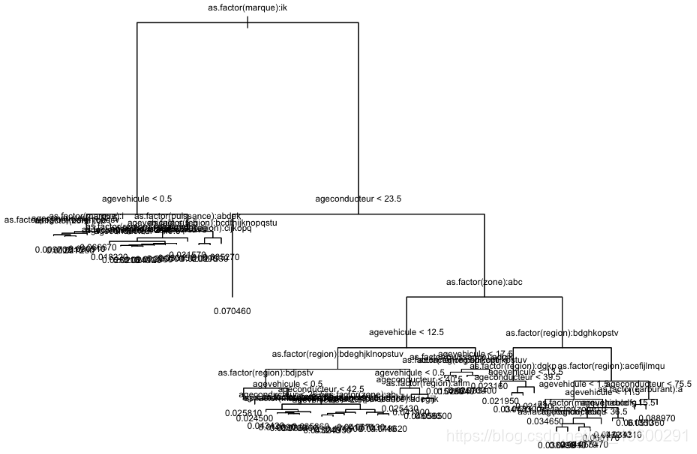
现在，每个分支都定义了一个类，可以使用它来定义一个类。应该被认为是同质的。
Class 6 average = 0.04010406 variance = 0.04424163
Class 8 average = 0.05191127 variance = 0.05948133
Class 9 average = 0.07442635 variance = 0.08694552
Class 10 average = 0.4143646 variance = 0.4494002
Class 11 average = 0.1917445 variance = 0.1744355
Class 15 average = 0.04754595 variance = 0.05389675
Class 20 average = 0.08129577 variance = 0.0906322
Class 22 average = 0.05813419 variance = 0.07089811
Class 23 average = 0.06123807 variance = 0.07010473
Class 24 average = 0.06707301 variance = 0.07270995
Class 25 average = 0.3164557 variance = 0.2026906
Class 26 average = 0.08705041 variance = 0.108456
Class 27 average = 0.06705214 variance = 0.07174673
Class 30 average = 0.05292652 variance = 0.06127301
Class 31 average = 0.07195285 variance = 0.08620593
Class 32 average = 0.08133722 variance = 0.08960552
Class 34 average = 0.1831559 variance = 0.2010849
Class 39 average = 0.06173885 variance = 0.06573939
Class 41 average = 0.07089419 variance = 0.07102932
Class 44 average = 0.09426152 variance = 0.1032255
Class 47 average = 0.03641669 variance = 0.03869702
Class 49 average = 0.0506601 variance = 0.05089276
Class 50 average = 0.06373107 variance = 0.06536792
Class 51 average = 0.06762947 variance = 0.06926191
Class 56 average = 0.06771764 variance = 0.07122379
Class 57 average = 0.04949142 variance = 0.05086885
Class 58 average = 0.2459016 variance = 0.2451116
Class 59 average = 0.05996851 variance = 0.0615773
Class 61 average = 0.07458053 variance = 0.0818608
Class 63 average = 0.06203737 variance = 0.06249892
Class 64 average = 0.07321618 variance = 0.07603106
Class 66 average = 0.07332127 variance = 0.07262425
Class 68 average = 0.07478147 variance = 0.07884597
Class 70 average = 0.06566728 variance = 0.06749411
Class 71 average = 0.09159605 variance = 0.09434413
Class 75 average = 0.03228927 variance = 0.03403198
Class 76 average = 0.04630848 variance = 0.04861813
Class 78 average = 0.05342351 variance = 0.05626653
Class 79 average = 0.05778622 variance = 0.05987139
Class 80 average = 0.0374993 variance = 0.0385351
Class 83 average = 0.06721729 variance = 0.07295168
Class 86 average = 0.09888492 variance = 0.1131409
Class 87 average = 0.1019186 variance = 0.2051122
Class 88 average = 0.05281703 variance = 0.0635244
Class 91 average = 0.08332136 variance = 0.09067632
Class 96 average = 0.07682093 variance = 0.08144446
Class 97 average = 0.0792268 variance = 0.08092019
Class 99 average = 0.1019089 variance = 0.1072126
Class 100 average = 0.1018262 variance = 0.1081117
Class 101 average = 0.1106647 variance = 0.1151819
Class 103 average = 0.08147644 variance = 0.08411685
Class 104 average = 0.06456508 variance = 0.06801061
Class 107 average = 0.1197225 variance = 0.1250056
Class 108 average = 0.0924619 variance = 0.09845582
Class 109 average = 0.1198932 variance = 0.1209162在这里，当根据索赔的经验平均值绘制经验方差时，我们得到
?
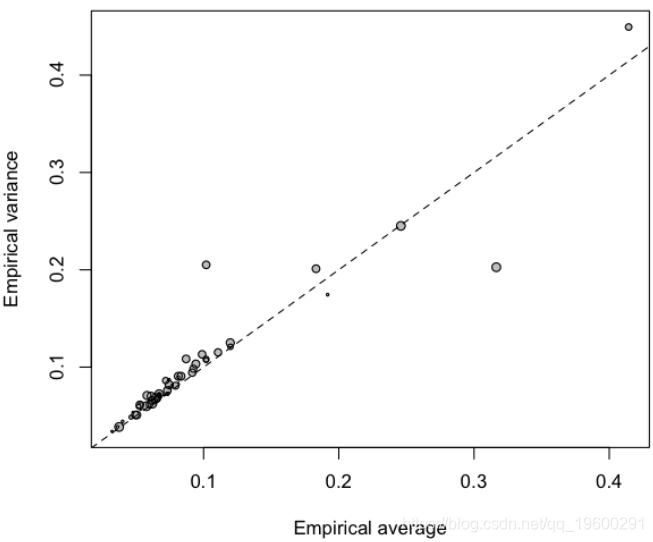
在这里，我们可以识别剩余异质性的类。
R语言广义线性模型索赔频率预测：过度分散、风险暴露数和树状图可视化
标签：rap svd handler text 必须 笛卡尔 intercept 点击 att
原文地址：https://www.cnblogs.com/tecdat/p/13230032.html
