标签:alt cup can 选择 就是 lower lse 比较 操作
引言:笔者看过几篇网上的扫描线算法教程,但是总觉得网上的博客讲的有疏漏。有一些性质博客作者认为它们显然成立,忽略了它们,而读者不明白这些性质的原理,被蒙在鼓里。扫描线算法的核心在于线段树的构建(毕竟要利用线段树加速计算),而线段树的构建是很多作者所没有介绍清楚的。扫描线的基本思想相对容易理解,而要想彻底弄清楚线段树的细节,可能会比较困难。本篇文章重点介绍扫描线线段树的构建,希望能让读者有更深入的理解。
本文的描述比较具体,但是过于形式化,尤其是算法有效性证明的部分。如果读者对代码中的每一句话都深信不疑,那么大可不用看算法有效性证明的部分。
在\(xOy\)平面,有\(n\)个矩形,它们的四边都平行于坐标轴
设每个矩形的左下角是\((x1,y1)\),右上角是\((x2,y2)\)
输入\(n\),以及\(n\)组\(x1,y1,x2,y2\)
输出这\(n\)个矩形的并的面积
矩形的坐标为\(double\)范围内的实数,\(n\le 100000\),限时\(1s\)解决
为了避免歧义,以下讨论的问题中,在直角坐标系中,以\(x\)轴的正方向为右,\(y\)轴的正方向为上。
平行于\(x\)轴的边叫上下边或水平边,平行于\(y\)轴的边叫左右边或竖直边。
所有的数组角标从\(1\)开始。
本文在推理时用了一些逻辑符号,其中\(\forall , \exists,\in\)分别表示任意...,存在...,...属于...
\(and,or\)分别是逻辑与和逻辑或,\(\to\)是蕴含运算,习惯上称为若...则...
逻辑表达式的值是\(true\)和\(false\),但是本文为了方便,令\(true=1,false=0\)
用线段树优化的扫描线算法时间复杂度为\(O(nlogn)\),空间复杂度为\(O(n)\)
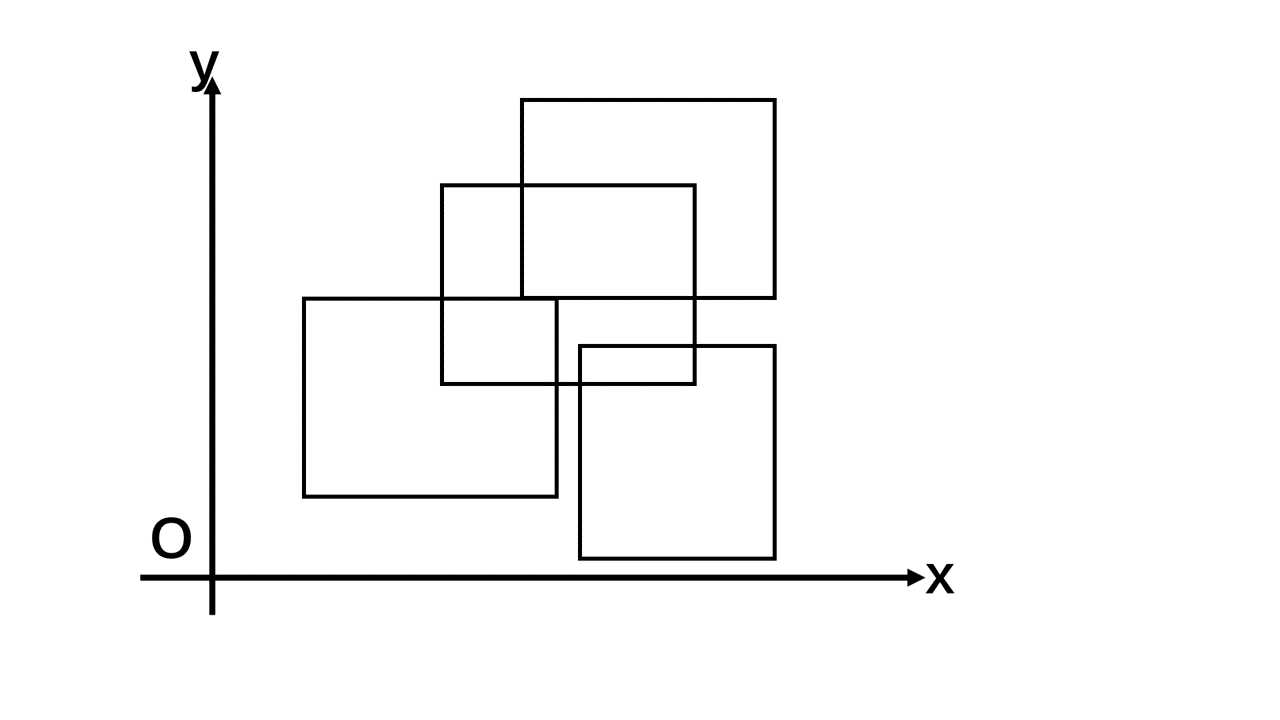
首先,我们要把二维的问题化为一维问题,即将矩形问题化为线段问题,学习过扫描线思想的读者可以选择性跳过。
定义如下结构体数组,数组大小>\(2n\)即可
struct edge
{
double x1,x2,y;
int flag;
}e[200010];
我们把矩形的左下角和右上角的信息转化为矩形的上下边的信息,即一个矩形可以由上边\((x1,x2,y1,-1)\)和下边\((x1,x2,y1,1)\)确定,那么一共有\(2n\)个这样的数对。
for(int i=1;i<=n;i++)
{
double x1,y1,x2,y2;
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);//左边横坐标、
e[2*i-1]=mp(x1,x2,y2,-1);//上边
e[2*i]=mp(x1,x2,y1,1);//下边
x[2*i-1]=x1;
x[2*i]=x2;
}
\(mp\)是一个生成4元数对的函数
edge mp(double x1,double x2,double y,int flag)
{
edge re;
re.x1=x1,re.x2=x2,re.y=y,re.flag=flag;
return re;
}
\(x1,x2,y\)分别对应水平线段的左端点横坐标、右端点横坐标、线段纵坐标
\(flag\)是上/下边属性,1意味着这是矩形的下边,-1意味着这是矩形的上边。
现在,我们对这\(2n\)个4元数对按照第三项升序排列。
int all=2*n;
sort(e+1,e+all+1,cmp_y);//按照y升序排列
注:
bool cmp_y(const edge a,const edge b)//定义"<"
{
return a.y<b.y;
}
我们把这\(2n\)条水平边所在直线称为扫描线,接下来要从下往上遍历\(2n\)条扫描线,我们可以直观地想象有一条水平的直线从下向上运动,这个运动的过程被称为扫描。这就是扫描线算法名字的由来。
扫描线算法的思路是沿着所有的扫描线 (共\(2n\)条),将矩形的并切成若干份图形,每一份图形都是若干个不相交的矩形,而且它们的上下边都分别共线。
我们可以用每一份图形在\(x\)轴上的投影长度*这一份对应的高度。其中对应的高度是比较好求的,只要用上下边的纵坐标相减即可,关键是每一份在\(x\)轴上的投影的长度。我们也可以把投影一词称为线段覆盖,简称覆盖,因为从一维的\(x\)轴上看,一个矩形的投影就好比一条与该矩形的宽相等长的线段覆盖在\(x\)轴上。我们认为一个区间可以被多条线段覆盖,这对应了多个矩形相交的情形。
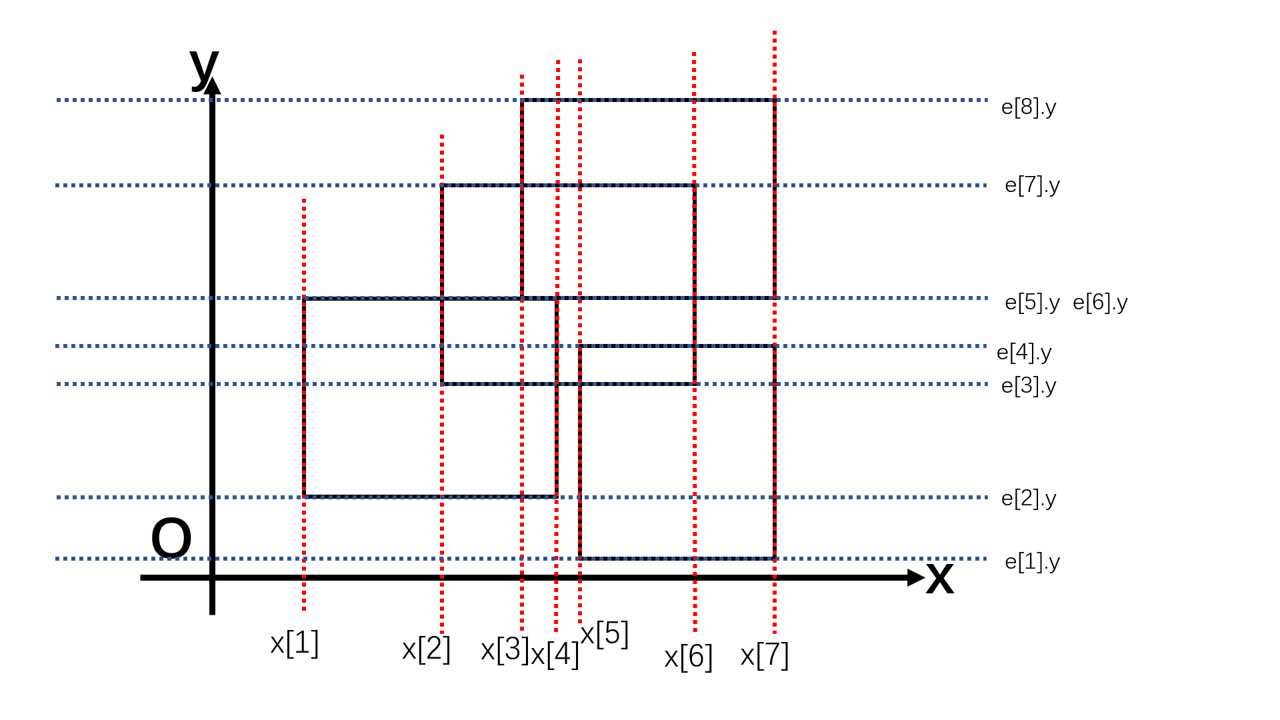
如图:将矩形面积并沿着7根蓝色水平虚线切割(当然,严格来说只有中间的5条线起了切割的作用)
第1份的面积是\((x[7]-x[5])*(e[2].y-e[1].y)\)
第2份的面积是\((x[4]-x[1]+x[7]-x[5])*(e[3].y-e[2].y)\)
第3份的面积是\((x[7]-x[1])*(e[4].y-e[3].y)\)
第4份的面积是\((x[6]-x[1])*(e[6].y-e[4].y)\)
第5份的面积是\((x[7]-x[2])*(e[7].y-e[6].y)\)
第6份的面积是\((x[7]-x[3])*(e[8].y-e[7].y)\)
累加求和即可
注意,图中\(e[5].y==e[6].y\),意味着两条扫描线共线,我们可以认为第5份面积是0。
我们可以把每一份图形的面积写成
第1份的面积是\((x[7]-x[5])*(e[2].y-e[1].y)\)
第2份的面积是\((x[4]-x[1]+x[7]-x[5])*(e[3].y-e[2].y)\)
第3份的面积是\((x[7]-x[1])*(e[4].y-e[3].y)\)
第4份的面积是\((x[6]-x[1])*(e[5].y-e[4].y)\)
第5份的面积是\((x[7]-x[2])*(e[6].y-e[5].y)=0\)
第6份的面积是\((x[7]-x[2])*(e[7].y-e[6].y)\)
第7份的面积是\((x[7]-x[3])*(e[8].y-e[7].y)\)
这样做保证严格有\(2n-1\)份图形,便于处理
\(x\)数组代表了竖直边的坐标,将所有的\(x1,x2\)加入到\(x\)数组中,排序,并去重即可
for(int i=1;i<=n;i++)
{
double x1,y1,x2,y2;
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);//左边横坐标、
e[2*i-1]=mp(x1,x2,y2,-1);//上边
e[2*i]=mp(x1,x2,y1,1);//下边
x[2*i-1]=x1;
x[2*i]=x2;
}
sort(x+1,x+all+1);//对横坐标排序
int k=1;//去重后x数组的元素个数
for(int i=2;i<=all;i++)
{
if(x[i]!=x[i-1])//去重
{
x[++k]=x[i];
}
}
之后取\(x\)数组的前\(k\)个元素即可,它们对应了\(x\)轴上的\(k\)个点
由\(k\)个点可以确定\(k-1\)个区间,称为单位区间
令\(a_i=[x[i],x[i+1]]\),称为第\(i\)单位区间
定义\(a_i=[x[i],x[i+1]],i<k\),用\(a_i\)表示第\(i\)单位区间,不考虑区间
我们在计算每一份图形在\(x\)轴上的投影,需要考虑\(a_i\)是否被覆盖
被覆盖就计算\(a_i\)的长度,即\(x[i+1]-x[i]\)
计算面积的程序是这样的:
double ans=0;
for(int i=1;i<all;i++)//不管最后一条边,因为最后一条边的上方没有矩形,对面积没有贡献
{
int l=lower_bound(x+1,x+k+1,e[i].x1)-x;
int r=lower_bound(x+1,x+k+1,e[i].x2)-x;
update(k,l,r-1,e[i].flag);
ans+=(e[i+1].y-e[i].y)*sum;
}
在主函数之外,还要定义\(update\)函数,这个放到后面讲。
int l=lower_bound(x+1,x+k+1,e[i].x1)-x;
int r=lower_bound(x+1,x+k+1,e[i].x2)-x;
这两句代码是在计算某条水平边的左、右端点分别对应\(x\)数组的第几个元素
即区间\([e[i].x1,e[i].x2]=\bigcup_{i=l}^{r-1} a_i\),换言之就是找到\([e[i].x1,e[i].x2]\)对应的是哪些连续的单位区间
然后我们修改这\(r-l\)个单位区间的“覆盖数量”
“覆盖数量”用\(cover\)数组来表达,\(cover\)是一个随\(i\)变化的数组
\(cover\)数组的定义为:
在用\(update\)函数处理完第\(i\)条扫描线的时候,\(cover[j]\)等于
\(x\in a_j\, and\, y\in [e[i].y,e[i+1].y]\)这个矩形区域被\(cover[j]\)个题目给定的矩形所覆盖,或者说单位区间\(a_j\)被\(cover[j]\)个线段所覆盖。

如图,在用\(update\)函数处理完第\(3\)条扫描线的时候
\(cover[1]=1,cover[2]=2,cover[3]=2,cover[4]=1,cover[5]=2,cover[6]=1\)
可以从图中看出,\(a_1,a_4,a_6\)只出现了一个矩形的投影,而\(a_2,a_3,a_5\)出现了两个矩形的投影
那么\(cover[j]>0\)即是被覆盖,\(cover[j]=0\)即是没有被覆盖。
\(cover\)的更新利用了差分求和的思想。
如果\(flag=1\),意味着遇到了一条矩形的下边,那么这个矩形在该下边的上方,即在
\(x\in [x[l],x[r]]\,and\,y\in [e[i].y,e[i+1].y]\)区域被一个新的矩形所覆盖,也可以想象区间\([x[l],x[r]]\)上增加了一条线段。
所以对于\(\forall \,l\le j<r,cover[j]++\)即可
如果\(flag=-1\),意味着遇到了一条矩形的上边,那么这个矩形在该上边的下方,即在
\(x\in [x[l],x[r]]\,and\,y\in [e[i].y,e[i+1].y]\)区域没有被这个矩形所覆盖,而在
\(x\in [x[l],x[r]]\,and\,y\in [e[i-1].y,e[i].y]\)区域被这个矩形所覆盖,也可以想象一条覆盖\([x[l],x[r]]\)区间的线段被删除了。
所以对于\(\forall \,l\le j<r,cover[j]--\)即可
将两种情况统一起来就是对于\(\forall \,l\le j<r,cover[j]+=flag\)
更新完\(cover\)数组,统计哪些区间被覆盖(\(cover[j]>0\)),计算长度即可
\(update\)的代码如下:
double sum=0;
int cover[200010];
void update(int k,int l,int r,int flag)
{
for(int i=l;i<=r;i++)
{
cover[i]+=flag;
}
sum=0;
for(int i=1;i<k;i++)
{
if(cover[i]>0)
{
sum+=x[i+1]-x[i];
}
}
}
以下是未优化的扫描线求矩形面积并的代码
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
struct edge
{
double x1,x2,y;
int flag;
}e[200010];
edge mp(double x1,double x2,double y,int flag)
{
edge re;
re.x1=x1,re.x2=x2,re.y=y,re.flag=flag;
return re;
}
bool cmp_y(const edge a,const edge b)
{
return a.y<b.y;
}
double x[200010];
double sum=0;
int cover[200010];
void update(int k,int l,int r,int flag)
{
for(int i=l;i<=r;i++)
{
cover[i]+=flag;
}
sum=0;
for(int i=1;i<k;i++)
{
if(cover[i]>0)
{
sum+=x[i+1]-x[i];
}
}
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
double x1,y1,x2,y2;
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
e[2*i-1]=mp(x1,x2,y2,-1);//上边
e[2*i]=mp(x1,x2,y1,1);//下边
x[2*i-1]=x1;
x[2*i]=x2;
}
int all=2*n;
sort(e+1,e+all+1,cmp_y);//按照y升序排列
sort(x+1,x+all+1);//对横坐标排序,以备离散化使用
int k=1;//去重后x数组的元素个数
for(int i=2;i<=all;i++)
{
if(x[i]!=x[i-1])
{
x[++k]=x[i];
}
}
//假设第i个单位区间为区间[ x[i],x[i+1] ]
//离散化后k个不同的端点横坐标映射到1~k共k个整数,一共k-1个单位区间
double ans=0;
for(int i=1;i<all;i++)//不管最后一条边,因为最后一条边的上方没有矩形,对面积没有贡献
{
int l=lower_bound(x+1,x+k+1,e[i].x1)-x;
int r=lower_bound(x+1,x+k+1,e[i].x2)-x;
update(k,l,r-1,e[i].flag);
ans+=(e[i+1].y-e[i].y)*sum;
}
printf("%.2lf\n",ans);
}
纵观上述代码,\(update\)这个函数是耗时的关键,每次\(update\)的时间复杂度为\(O(n)\),累计为\(O(n^2)\)
所以我们可以设计一个数据结构来处理这个问题,用线段树即可。我们需要把所有\(cover[j]>0\)的区间\(a_j\)的长度累加求和。
本问题所用线段树与常见的线段树不同,没有接触过线段树的读者可以先学习支持单点修改、区间求和的线段树,了解线段树的基本性质。
设有一个序列\(cover_j\),还有一个序列\(weight_j\)(代表单位区间的长度)
1.定义第\(i\)次更新操作($ l_i,r_i,flag_i \(),\)l \le r$
为\(\forall j \in [l_i,r_i],cover_j+=flag_i\),其中\(flag_i=1,-1\)
2.定义查找操作,该操作没有参数
为求\(\sum_{j=1}^{k-1}weight_j*(cover_j>0)\),其中\(cover_j>0\)为逻辑表达式,真值为实数1,假值为实数0
(注:\(k-1\)即单位区间的个数,\(k\)是区间的端点总数,两者差1)
3.每一次操作的时间复杂度为\(O(log\,n)\)
其中操作1对应着更新单位区间的线段覆盖状况以及单位区间的线段覆盖长度,操作2对应着求总区间的线段覆盖长度。
设有一个序列\(cover_j\),还有一个序列\(weight_j\)
1.定义第\(i\)次更新操作($ l_i,r_i,flag_i \(),\)l \le r$
为\(\forall j \in [l_i,r_i],cover_j+=flag_i\),其中\(flag_i=1,-1\)
该条件对应着一个矩形具有上下两条边,它们的左右端点横坐标是对应相等的,而标记上下边的 \(flag\) 又是相反的。
注:\(\to\)是若...则...的意思
2.定义查找操作,该操作没有参数
为求\(\sum_{j=1}^{k-1}weight_j*(cover_j>0)\),其中\(cover_j>0\)为逻辑表达式,真值为实数1,假值为实数0
3.每一次操作的时间复杂度为\(O(log\,n)\)
也就是说,追加的那个条件对线段树有着重要的影响。
我们要设计的线段树基于后者的追加条件。
下面给出线段树的代码以及原理说明
struct tree
{
double sum;
int cover;
int l,r;
}seg[800010];//数组大小>单位区间数量的4倍
void build(int o,int l,int r)
{
seg[o].cover=0;
seg[o].sum=0;
seg[o].l=l;
seg[o].r=r;
if(l==r)return;
int mid=(l+r)/2;
build(o*2,l,mid);
build(o*2+1,mid+1,r);
}
void pushup(int o)
{
if(seg[o].cover)
{
seg[o].sum=x[seg[o].r+1]-x[seg[o].l];//第r单位区间的右端点是x[r+1]
}
else if(seg[o].l<seg[o].r)//不是线段树的叶节点
{
seg[o].sum=seg[o*2].sum+seg[o*2+1].sum;
}
else//是线段树的叶节点
{
seg[o].sum=0;
}
}
void update(int o,int l,int r,int flag)
{
if(seg[o].l==l&&seg[o].r==r)
{
seg[o].cover+=flag;
pushup(o);
return ;
}
int mid=(seg[o].l+seg[o].r)/2;
if(r<=mid)
{
update(o*2,l,r,flag);
}
else if(l<=mid)
{
update(o*2,l,mid,flag);
update(o*2+1,mid+1,r,flag);
}
else
{
update(o*2+1,l,r,flag);
}
pushup(o);
}
线段树在\(main()\)中的调用
build(1,1,k-1);//构建线段树
double ans=0;
for(int i=1;i<all;i++)//不管最后一条边,因为最后一条边的上方没有矩形,对面积没有贡献
{
int l=lower_bound(x+1,x+k+1,e[i].x1)-x;
int r=lower_bound(x+1,x+k+1,e[i].x2)-x;
//对应单位区间l~r-1的并
update(1,l,r-1,e[i].flag);
ans+=(e[i+1].y-e[i].y)*seg[1].sum;
}
一次\(update\)可以更新\(seg[1].sum\)的值,该值就是我们希望求解的全部\(k-1\)个区间上的覆盖长度。
这里要声明一下,在结构体 \(seg[o]\) 中,\(o\)代表线段树节点的编号,它的成员变量\(l,r\)代表这个节点对应第\(l\)到\(r\)号单位区间。\(cover\)与\(sum\)的定义相对复杂,以下是相关的定义。
先定义线段树访问集\(A_i\):
在\(main()\)中第\(i\)次调用\(update\)之后,\(update\)自身递归有限多次。
若某一次\(update(o,l,r,flag)\)的参数满足\(seg[o].l=l\,and\,seg[o].r=r\)时,即触发\(return\)时
则令\(o\in A_i\)
形象地说\(A_i\)里面的元素就是线段树上的节点编号,这些节点对应的区间是连续的,它体现了线段树如何用\(O(log\,n)\)的时间复杂度去分割单位区间\(l\)到\(r-1\)

比如,第1次在\(main()\)中调用\(update(1,5,6,1)\),修改的单位区间是5,6
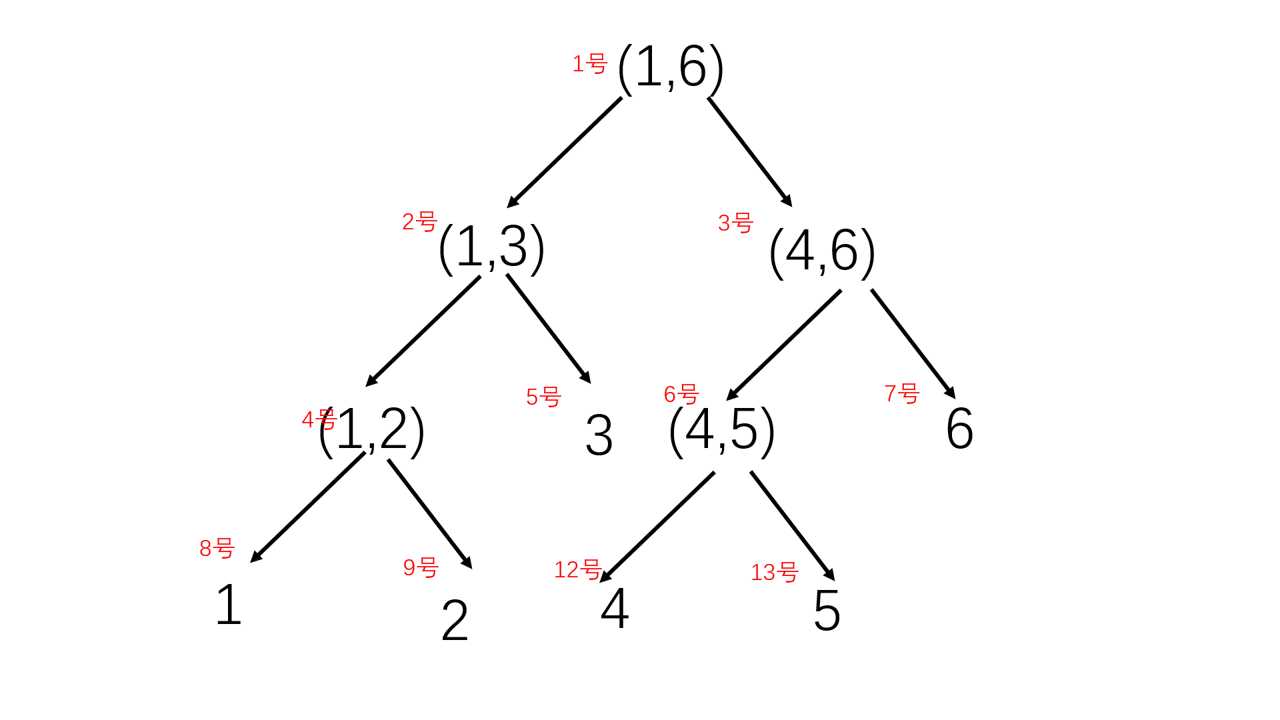
由图,对应的\(A_1=\{7,13\}\),表示线段树的7号节点对应\(a_6\),13号节点对应\(a_5\)
第2次\(update(1,1,3,1)\) \(A_2=\{2\}\)
第3次\(update(1,2,5,1)\) \(A_3=\{5,6,9\}\)
第4次\(update(1,5,6,-1)\) \(A_4=\{7,13\}\)
第5次\(update(1,1,3,-1)\) \(A_5=\{2\}\)
第6次\(update(1,3,6,1)\) \(A_6=\{3,5\}\)
第7次\(update(1,2,5,-1)\) \(A_7=\{5,6,9\}\)
第8条边上方没有图形,在算法中不予考虑,假如考虑第8条边,\(A_8=\{3,5\}\)
可以发现\(A_1=A_4\),\(A_2=A_5\),\(A_3=A_7\),\(A_6=A_8\),这体现了每一个矩形都有两条对称的上下边。
有了\(A_i\)的定义,我们可以定义\(seg[o].cover\)。
由于\(seg[o].cover\)与\(seg[o].sum\)都是不断更新的,所以它们的定义是动态的。
假设程序在\(main()\)中调用了\(now\)次\(update\),即在\(for\)循环中,当前的\(i=now\)、
\(seg[o].cover\)的定义:
\(seg[o].cover=\sum_{i=1}^{now}(o\in A_i)e[i].flag\)
\((o\in A_i)\)是逻辑表达式,真值为实数1,假值为实数0
为了简便地说明\(seg[o].sum\),再引入关系$sub(x,y)=\exists t\in N,x=\lfloor \frac{y}{2^t} \rfloor $
表示以\(x\)节点为根的子树中有\(y\)节点(\(y\)可以为\(x\)),或者说\(x\)是\(y\)的祖先(或自身)
定义函数\(leaf(l)\):\(\forall o\,seg[o].l=seg[o].r\to leaf(l)=o\)
表示一个叶节点\(o\)对应单位区间\(a_l\),该映射的反函数是\(leaf(l)\)
\(seg[o].sum\)的定义:
\(seg[o].sum=\sum_{i=seg[o].l}^{seg[o].r} \exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
其中\(\exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))\)是一个逻辑表达式
$seg[o].sum $的定义比较复杂,形象地来说就是:
假设现在编号\(seg[o].l\)到\(seg[o].r\)的单位区间都没有被覆盖,对于\(o\)的所有子孙节点\(j\)(含自身),如果\(seg[j].cover>0\),那么对编号\(seg[j].l\)到\(seg[j].r\)的单位区间进行一次覆盖,
最后\(seg[o].sum\)是上述所有区间的覆盖长度,保证每次用\(update\)修改后\(seg[o].sum\)都满足定义。
也就是说\(seg[o].sum\)只关心以\(o\)为根的子树的情况,不关心\(o\)节点的祖先所对应区间是否被某一线段完全覆盖。假如某一线段覆盖了节点1对应的区间\(a_1\)到\(a_6\),那么\(seg[2].sum\)不会更新,而真实的覆盖情况是\(a_1\)到\(a_3\)全被覆盖。
如果\(o \ne 1\),那么\(seg[o].sum\)不能反映单位区间\(a_{seg[o].l}\)到\(a_{seg[o].r}\)上真实的覆盖长度。如果\(o=1\),\(seg[1].sum\)可以反映全部区间的覆盖长度。
下面将根据代码来证明相关函数可以维护\(cover\)和\(sum\)两个参数。
if(seg[o].l==l&&seg[o].r==r)
{
seg[o].cover+=flag;
pushup(o,l,r);
return ;
}
从\(update\)函数的代码中可以看出,只有满足\(seg[o].l=l\,and\,seg[o].r=r\)时,\(seg[o].cover+=flag\)
与\(seg[o].cover\)定义相符
\(seg[o].cover=\sum_{i=1}^{now}(o\in A_i)e[i].flag\)
由于\(\forall i\,e[i].flag=-1 \to \exists m<i\,e[m].flag=1\,and\,l_i=l_m,r_i=r_m\)
这意味着\(seg[o].cover=\sum_{i=1}^{now}(o\in A_i)e[i].flag \ge 0\),这体现了区间覆盖的非负性
设区间\(a_j\)所对应的叶节点为\(o^{‘}\),即\(o^{‘}=leaf(j)\)
则区间\(a_j\)真实的覆盖数量为:
\(\sum_{\forall o\,sub(o,o^{‘})}\sum_{i=1}^{now}(o\in A_i)e[i].flag\)
\(=\sum_{\forall o\,sub(o,o^{‘})}seg[o].cover\)
\(\ge seg[o].cover\)
其中,\(o\)是\(o^{’}\)的任意一个祖先(含自身)
从\(pushup\)的代码可以看出\(seg[o].sum\)具有递归结构,我们可以用结构归纳法证明,证明的规则有2条:
1.任取一个有子命题的命题,若递归的子命题成立,则原命题成立
2.任取一个没有子命题的命题,都成立
满足这2条,所有的命题都成立。
证明:
void pushup(int o)
{
if(seg[o].cover)//cover不为0
{
seg[o].sum=x[seg[o].r+1]-x[seg[o].l];//第r单位区间的右端点是x[r+1]
}
else if(seg[o].l<seg[o].r)//cover=0且o不是线段树的叶节点
{
seg[o].sum=seg[o*2].sum+seg[o*2+1].sum;
}
else//cover=0且o是线段树的叶节点
{
seg[o].sum=0;
}
}
这\(pushup\)虽然没有用到递归,但是如果我们把\(seg[o].sum\)看成一个一元函数,根据代码可以递归地写出它的定义:
先证明规则1:
如果\(o\)不是叶节点,即\(seg[o].l<seg[o].r\)
(1)如果\(seg[o].cover>0\),说明
\(\forall\,i\,seg[o].l\le i\le seg[o].r\),令\(o^{‘}=leaf(i)\),那么\(o^{‘}\)是一个叶节点,一定在以\(o\)为根的子树中,此时\(sub(o,o^{‘})\)成立
则
\(\sum_{i=seg[o].l}^{seg[o].r} \exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
\(\because (sub(o,o)\,and\,sub(o,leaf(i))\,and\,(seg[o].cover>0))=1\)
\(\therefore \exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))=1\)
上式\(=\sum_{i=seg[o].l}^{seg[o].r} (x[i+1]-x[i])\)
\(=\sum_{i=seg[o].l}^{seg[o].r}(x[i+1]-x[i])\)
\(=x[seg[o].r+1]-x[seg[o].l]\)
那么根剧\(seg[o].sum\)的递归定义
可知\(seg[o].sum=x[seg[o].r+1]-x[seg[o].l]\)
即
\(seg[o].sum=\sum_{i=seg[o].l}^{seg[o].r} \exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
(2)如果\(seg[o].cover=0\)
假设\(o_1=o*2,o_2=o*2+1\),为\(o\)节点的两个子节点
那么若\(o_1,o_2\)满足条件
即
\(seg[o_1].sum=\sum_{i=seg[o_1].l}^{seg[o_1].r} \exists j(\,sub(o_1,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
\(seg[o_2].sum=\sum_{i=seg[o_2].l}^{seg[o_2].r} \exists j(\,sub(o_2,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
我们不妨先计算下列求和式:
\(\sum_{i=seg[o].l}^{seg[o].r} \exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
\(=\sum_{i=seg[o_1].l}^{seg[o_1].r} \exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
\(+\sum_{i=seg[o_2].l}^{seg[o_2].r} \exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
对等号后面的第一个求和式中的\(\exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))\)等价变换
\(\Leftrightarrow \exists j(\,(sub(o_1,j)or\,j=o)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))\)
\(\Leftrightarrow \exists j(\,(sub(o_1,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))or((j=o)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))\)
\(\Leftrightarrow \exists j(\,(sub(o_1,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))or(sub(o,leaf(i))\,and\,(seg[o].cover>0))\)
\(\because seg[o].cover=0\)
\(\therefore (sub(o,leaf(i))\,and\,(seg[o].cover>0))=0\)
\(\exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))\)
\(\Leftrightarrow (\exists j\,(sub(o_1,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))or(sub(o,leaf(i))\,and\,(seg[o].cover>0))\)
\(=\exists j\,(sub(o_1,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))\)
\(\therefore \sum_{i=seg[o_1].l}^{seg[o_1].r} \exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
\(=\sum_{i=seg[o_1].l}^{seg[o_1].r} \exists j(\,(sub(o_1,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0)) (x[i+1]-x[i])\)
\(=seg[o_1].sum\)
同理
\(\therefore \sum_{i=seg[o_2].l}^{seg[o_2].r} \exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
\(=seg[o_2].sum\)
那么根剧\(seg[o].sum\)的递归定义
可知\(seg[o].sum=seg[o_1].sum+seg[o_2].sum\)
即
\(seg[o].sum=\sum_{i=seg[o].l}^{seg[o].r} \exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
然后证明规则2:
如果\(o\)是叶子节点
(1)\(cover[o]>0\)
与规则1的(1)同理,可以证明
\(seg[o].sum =\sum_{i=seg[o].l}^{seg[o].r} \exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
(2)\(cover[o]=0\)
\(\sum_{i=seg[o].l}^{seg[o].r} \exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
\(=\exists j(\,sub(o,j)\,and\,sub(j,leaf(seg[o].l))\,and\,(seg[j].cover>0))(x[seg[o].l+1]-x[seg[o].l])\)
\(\because o\)是叶节点
$\therefore \(上式\)=(seg[j].cover>0)(x[seg[o].l+1]-x[seg[o].l])=0$
那么根剧\(seg[o].sum\)的递归定义
可知
\(seg[o].sum=0=\sum_{i=seg[o].l}^{seg[o].r} \exists j(\,sub(o,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
综上两条规则均成立
所以这个算法可以正确维护\(seg[o].sum\)的值
\(seg[1].sum=\sum_{i=seg[1].l}^{seg[1].r} \exists j(\,sub(1,j)\,and\,sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
\(=\sum_{i=1}^{k-1} \exists j(sub(j,leaf(i))\,and\,(seg[j].cover>0))(x[i+1]-x[i])\)
将求和式中的逻辑表达式单独拿出来分析
\(\exists j(sub(j,leaf(i))\,and\,(seg[j].cover>0))\)
对于扫描线问题来说,我们关心每一个单位区间\(a_i\)的真实覆盖数量
它的值是:
\(\sum_{\forall o\,sub(o,o^{‘})}seg[o].cover\)
其中,\(o^{‘}=leaf(i)\)
若该值\(>0\)则该区间被覆盖,\(=0\)则没有覆盖
若该值\(>0\),则
\(\sum_{\forall o\,sub(o,o^{‘})}seg[o].cover>0\)
\(\therefore \exists j,sub(j,leaf(i))and(seg[j].cover>0)\)成立
即该区间被覆盖时,表达式的值为1
若该值\(=0\),则
\(\sum_{\forall o\,sub(o,o^{‘})}seg[o].cover=0\)
\(\therefore \forall j,sub(j,leaf(i))and(seg[j].cover=0)\)成立
\(\therefore \exists j,sub(j,leaf(i))and(seg[j].cover>0)\)不成立
即该区间未被覆盖时,表达式的值为0
\(\therefore a_i区间被覆盖\Leftrightarrow \exists j,sub(j,leaf(i))and(seg[j].cover>0)\)
\(\therefore seg[1].sum=\sum_{i=1}^{k-1} (a_i区间被覆盖)(x[i+1]-x[i])\)
即为所求
以上证明了算法的有效性,基本的思路是观察代码,然后给\(seg[o].sum\)和\(seg[o].cover\)提出数学意义上的解释。笔者实在是没有找到更好的解释办法,尝试过的简单的解释都出现了错误。最后贴出详细的代码。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
struct edge
{
double x1,x2,y;
int flag;
}e[200010];
edge mp(double x1,double x2,double y,int flag)
{
edge re;
re.x1=x1,re.x2=x2,re.y=y,re.flag=flag;
return re;
}
bool cmp_y(const edge a,const edge b)
{
return a.y<b.y;
}
double x[200010];
struct tree
{
double sum;
int cover;
int l,r;
}seg[800010];
void build(int o,int l,int r)
{
seg[o].cover=0;
seg[o].sum=0;
seg[o].l=l;
seg[o].r=r;
if(l==r)return;
int mid=(l+r)/2;
build(o*2,l,mid);
build(o*2+1,mid+1,r);
}
void pushup(int o)
{
if(seg[o].cover)
{
seg[o].sum=x[seg[o].r+1]-x[seg[o].l];//第r单位区间的右端点是x[r+1]
}
else if(seg[o].l<seg[o].r)//不是线段树的叶节点
{
seg[o].sum=seg[o*2].sum+seg[o*2+1].sum;
}
else//是线段树的叶节点
{
seg[o].sum=0;
}
}
void update(int o,int l,int r,int flag)
{
if(seg[o].l==l&&seg[o].r==r)
{
seg[o].cover+=flag;
pushup(o);
return ;
}
int mid=(seg[o].l+seg[o].r)/2;
if(r<=mid)
{
update(o*2,l,r,flag);
}
else if(l<=mid)
{
update(o*2,l,mid,flag);
update(o*2+1,mid+1,r,flag);
}
else
{
update(o*2+1,l,r,flag);
}
pushup(o);
}
int main()
{
freopen("rectangle.txt","r",stdin);
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
double x1,y1,x2,y2;
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
e[2*i-1]=mp(x1,x2,y2,-1);//上边
e[2*i]=mp(x1,x2,y1,1);//下边
x[2*i-1]=x1;
x[2*i]=x2;
}
int all=2*n;
sort(e+1,e+all+1,cmp_y);//按照y升序排列
sort(x+1,x+all+1);//对横坐标排序,以备离散化使用
int k=1;//去重后x数组的元素个数
for(int i=2;i<=all;i++)
{
if(x[i]!=x[i-1])
{
x[++k]=x[i];
}
}
//假设第i个单位区间为区间[ x[i],x[i+1] ]
//离散化后k个不同的端点横坐标映射到1~k共k个整数,一共k-1个单位区间
build(1,1,k-1);
double ans=0;
for(int i=1;i<all;i++)//不管最后一条边,因为最后一条边的上方没有矩形,对面积没有贡献
{
int l=lower_bound(x+1,x+k+1,e[i].x1)-x;
int r=lower_bound(x+1,x+k+1,e[i].x2)-x;
//对应单位区间l~r-1的并
update(1,l,r-1,e[i].flag);
ans+=(e[i+1].y-e[i].y)*seg[1].sum;
}
printf("%.2lf\n",ans);
}
标签:alt cup can 选择 就是 lower lse 比较 操作
原文地址:https://www.cnblogs.com/ssdfzhyf/p/13236273.html