标签:ima 不同的 一个 包含 要求 arch 关系 sql 生产
?
?
二分查找的时间复杂度是O(log2n),是一种很高效的查询方式。在一系类树种使用二分查找的树有很多,但并不是所有树都适合作为索引的结构。
?
性质:
但二叉搜索树不一定是"平衡的",它有可能退化成一条链表,那么他的搜索时间就变成了O(n)。
?
为了避免退化成一条链表,人们提出了二叉搜索树,AVL在二叉搜索树的基础上增加了约束:
每个节点的左子树和右子树的高度差不能超过1
也就是说要求节点的左右子树仍然为平衡二叉树。
常见的平衡二叉树有很多种,包括了AVL树、红黑树、数堆、伸展树。AVL树是最早提出来的自AVL树,当我们提到平衡二叉树时一般指的就是AVL树
左右平衡后就使得搜索时间复杂度能稳定在O(log2n)。
但是即便在理论上它的搜索效率高且比较稳定,但是由于“每访问一次节点就需要进行一次磁盘I/O操作”,在实际情况中只有两个子节点的情况下,树的高度依然有可能会很高,比如说现有一个五层共31个节点的树,那么我们需要进行5次I/O操作。
?
既然"二叉"结构可能让树变得很高,那么我们自然而然地就明白可以让子节点数变得更多来减少I/O次数。在文件系统和部分数据库系统中,B树就已经得到了实际的应用。
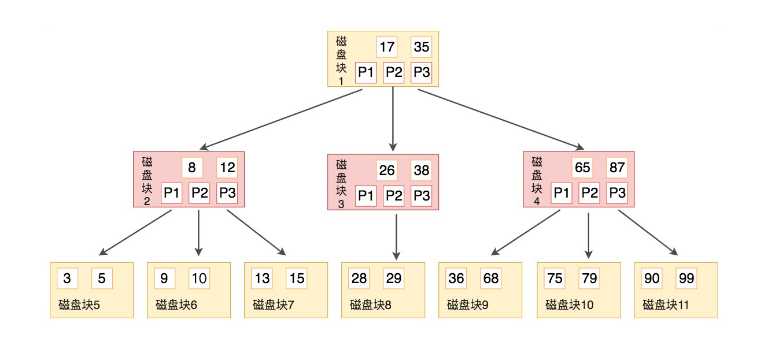
如图所示,B树有如下性质
B树也是平衡的,每个节点可以有M个子节点,M也称为B树的阶
每个磁盘块都包含着关键字和指针,有k-1个关键字,那么就有k个指针,也就是k个子节点。也就等同于子节点的数量=关键字数量+1
所有子节点都在同一层,且每个叶子节点没有子节点,只包含k-1个关键字
子节点和非子节点都即保存数据记录又保存索引。
k-1个关键字相当于划分出了k个范围,每个范围对应一个指针。
例如,有关键字Key[1], Key[2], …, Key[k-1],且关键字按照升序排序
它们划分出k个范围对应k个指针,P[1], P[2], …, P[k]
对应关系就是:P[1]指向关键字小于 Key[1]的子树,P[i]指向关键字属于 (Key[i-1], Key[i]) 的子树,P[k]指向关键字大于 Key[k-1]的子树
在B树上的搜索过程就是:
这里说的关键字在实际的数据库中,其实就是一条实际的数据或者主键值,详细可见此处
MongoDB内部使用的就是B树
?
主流的RDMS大多采用B+树作为索引结构,包括MySQL的InnoDB引擎(不同存储引擎的索引的工作方式并不一样。而即使多个存储引擎支持同一种类型的索引,其底层的实现也可能不同)
在数据结构性质上与B树不同的是:
?
上面说了两种数据结构性质上的不同,下面里对比下实际生产中两种索引结构的区别。
B+树查询效率更稳定。
B+树所有的数据记录都在叶子节点,而B树的数据记录可能在叶子节点也可能在非叶子节点,这样就会导致查询效率的不稳定。
B+树查询效率更高。
B+树的内部节点并没有指向关键字具体信息的指针,因此其内部节点相对B树更小。那么盘块所能容纳的关键字数量也越多,一次性读入内存的需要查找的关键字也就越多,相对IO读写次数就降低了。
B+树的范围查询效率更高。
B+树所有叶子节点都通过双向链表进行查询,方便范围查询。
而B树因为在非叶子节点中也存有数据记录,因此范围查询时需要通过对树的中序遍历才能完成
?
标签:ima 不同的 一个 包含 要求 arch 关系 sql 生产
原文地址:https://www.cnblogs.com/G-Aurora/p/13243476.html