标签：use oid 归并 algo lld ++ ons for ima
算法时间复杂度：妥妥的nlogn
步骤：
1.确定分界点 mid = (l+r) >> 1
2.递归排序左右两边
3.归并——合二为一（用两个指针，分别指向两个序列）
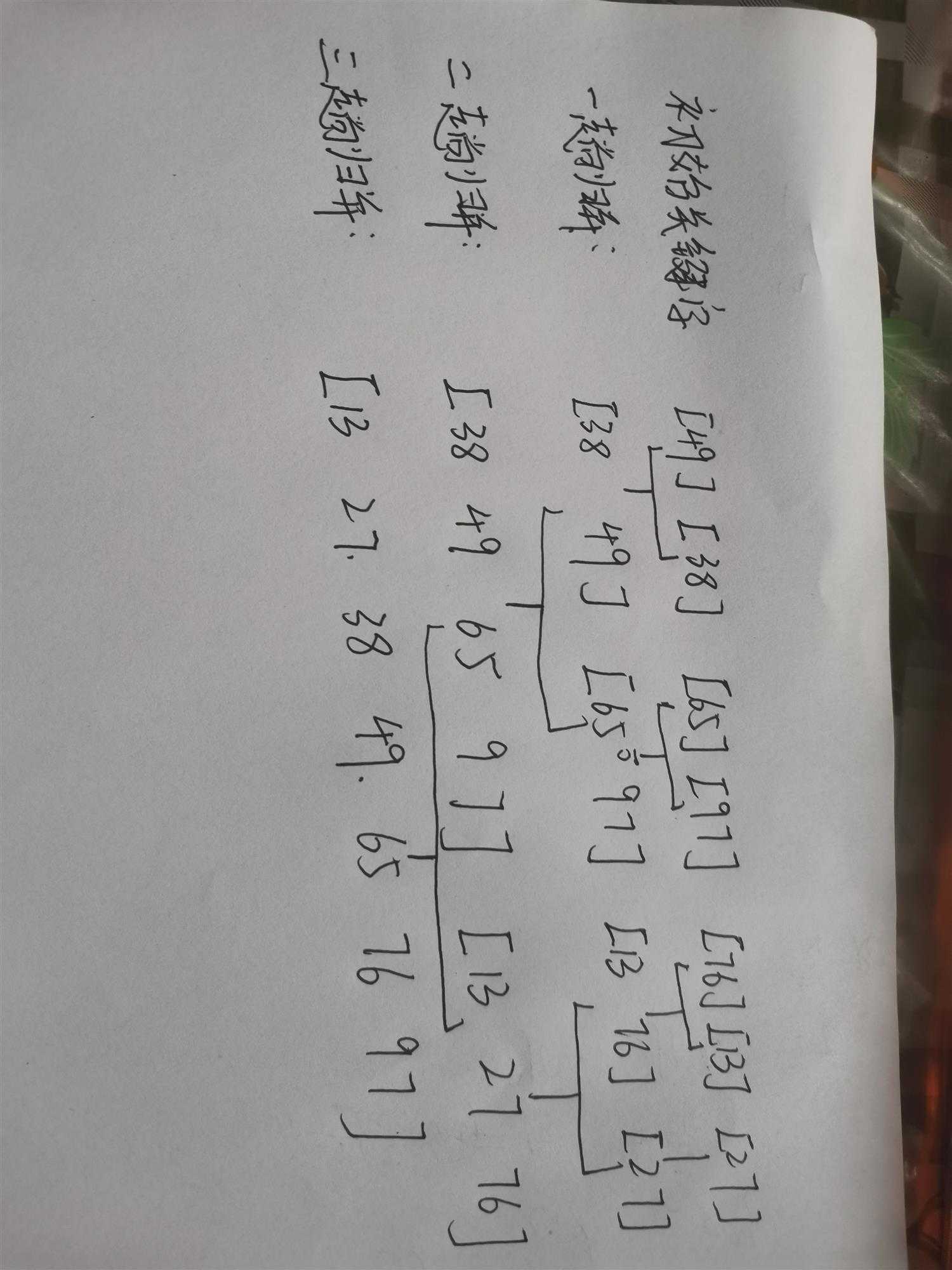就是递归到最底部，然后对小部分排序，归并为大部分。
代码模板：
1 void merge_sort(int q[], int l, int r) 2 { 3 if(l >= r) return; 4 5 int mid = (l + r) >> 1; 6 merge_sort(q, l, mid), merge_sort(q, mid+1, r); //递归两路 7 8 int k = 0, i = l, j = mid+1; 9 while(i <= mid && j <= r) 10 { 11 if(q[i] <= q[j]) tmp[k++] = q[i++]; 12 else tmp[k++] = q[j++]; 13 } 14 15 while(i <= mid) tmp[k++] = q[i++]; //补全剩余的 16 while(j <= r) tmp[k++] = q[j++]; 17 for(int i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j]; 18 }
总的代码：
1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 5 const int n = 5000000; 6 int q[n], tmp[n]; 7 8 void merge_sort(int q[], int l, int r) 9 { 10 if(l >= r) return; 11 12 int mid = (l + r) >> 1; 13 merge_sort(q, l, mid), merge_sort(q, mid+1, r); 14 15 int k = 0, i = l, j = mid+1; 16 while(i <= mid && j <= r) 17 { 18 if(q[i] <= q[j]) tmp[k++] = q[i++]; 19 else tmp[k++] = q[j++]; 20 } 21 22 while(i <= mid) tmp[k++] = q[i++]; 23 while(j <= r) tmp[k++] = q[j++]; 24 for(int i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j]; 25 } 26 27 int main() 28 { 29 int a, t; 30 31 scanf("%d %d", &a, &t); 32 for(int i = 0; i < a; i++) scanf("%d", &q[i]); 33 34 merge_sort(q, 0, a-1); 35 36 printf("%d", q[t]); 37 system("pause"); 38 return 0; 39 }
还发现了一个黑科技， nth_element() 函数
第二个参数是一个指向第 n 个元素的迭代器。如果这个范围内的元素是完全有序的，nth_dement() 的执行会导致第 n 个元素被放置在适当的位置。这个范围内，在第 n 个元素之前的元素都小于第 n 个元素，而且它后面的每个元素都会比它大。算法默认用 < 运算符来生成这个结果, 第 n 个元素之前的元素都小于它，但不必是有序的。同样，第 n 个元素后的元素都大于它，但也不必是有序的。
例如模板题：
第k小的数
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 6 long long q[5000010]; 7 8 int main() 9 { 10 long long a, t; 11 12 scanf("%lld %lld", &a, &t); 13 for(int i = 0; i < a; i++) scanf("%lld", &q[i]); 14 15 nth_element(q, q+t, q+a); 16 17 printf("%lld", q[t]); 18 return 0; 19 }
这个题因为数据有点大，所以用归并与快排都超时了，用这个函数却不会。
标签：use oid 归并 algo lld ++ ons for ima
原文地址：https://www.cnblogs.com/ZhengLijie/p/13246568.html
