标签:一起 binary 存在 计算机 back mamicode 产生 原码 问题
一、所有相关的码解释
(1)正数的原码=反码=补码
负数原码=>最高位表示符号位,其余位为真值
负数反码=>符号位不变,其他位取反
负数补码=>反码+1
移码=>移码(又叫增码)是符号位取反的补码,一般用指数的移码减去1来做浮点数的阶码,引入的目的是为了保证浮点数的机器零为全0.
综合练习: 求-11的原码、补码、反码(8位表示)

二、浮点数运算失去精度原因
(1)浮点数的表示方法

(2)IEEE754(英语发音读I tri for E)标准浮点数
因为读IEEE很难发音且容易读错,所以学术界一般读做 I triple for E(意思是IEEE); IEEE二进制浮点数算术标准(IEEE 754)是20世纪80年代以来最广泛使用的浮点数运算标准,为许多CPU与浮点运算器所采用。Reference: https://zh.wikipedia.org/wiki/IEEE_754

(3)IEEE754标准浮点数例题1

(4)IEEE754标准浮点数例题2

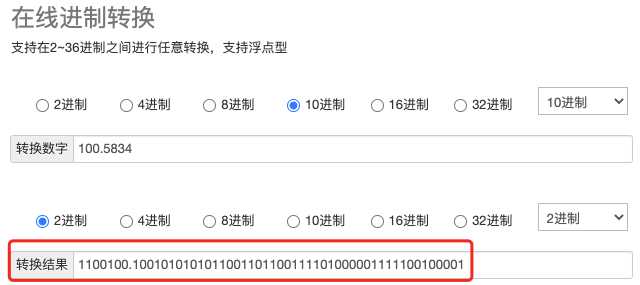
(5)练习题1: 将100.5834化为IEEE754标准单精度浮点数?
<1>首先把100.5834转成二进制为1100100.1001(为了便于手动运算,所以取小数点后四位,但为存在精度损失,取的越多精度越高,取四位后其实变成了100.5625),
这就是为什么浮点数在运算时不同的编程语言都会存在精度损失的原因!!!
https://tool.oschina.net/hexconvert
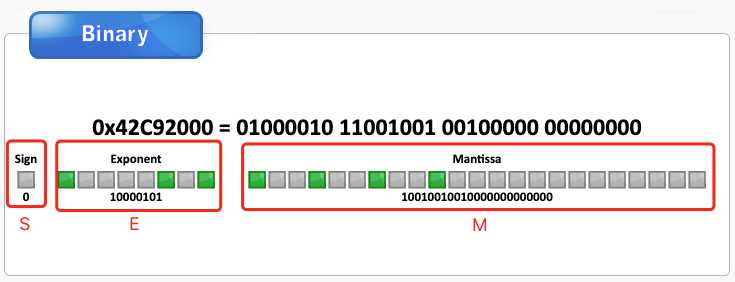
答案:

验证网站: http://www.binaryconvert.com/result_float.html?decimal=049048048046053054050053
附:浮点数的表示范围和溢出

<1>标准
http://grouper.ieee.org/groups/754/
<2>单精度浮点数内存中编码:
https://www.h-schmidt.net/FloatConverter/IEEE754.html
<3>双精度浮点数内存中编码:
http://www.binaryconvert.com/convert_double.html
标签:一起 binary 存在 计算机 back mamicode 产生 原码 问题
原文地址:https://www.cnblogs.com/arun-python/p/13247033.html