重新整理数据结构与算法(c#)—— 堆排序[二十一]

标签：数据结构   大顶堆   lang   public   制作   load   最大的   key   第一个   

前言

将下面按照从小到大排序:

int[] arr = { 4, 6, 8, 5, 9 };

这时候可以通过冒泡排序，计数排序等。

但是一但数据arr很大，那么会产生排序过于缓慢，堆排序就是一个很好的解决方案。

树的堆，有最大堆和最小堆。

看下最大堆:

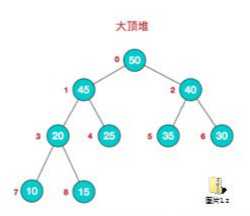
它是这样子的，就是说一个节点的大小一定大于它的左节点和右节点大小。

如何利用最大堆。进行从大到小的排序呢?

细节

细节如下:

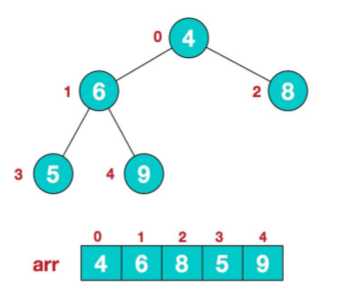
假如堆排序后：

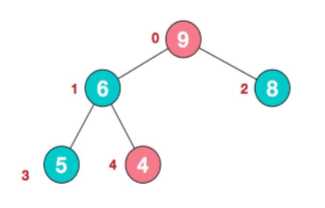
那么用root(根节点，最大节点)和最后一个数组元素进行交换，那么下次进行堆排序的元素就是length-1个，就不用管最后一个元素，因为最后一个元素已经排好序，且最大。

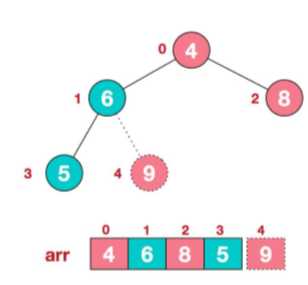
那么现在回到一个问题上了，就是如何进行最大堆排序呢？

有如下步骤:

1.找到树的最后非叶子节点。arr.length/2-1

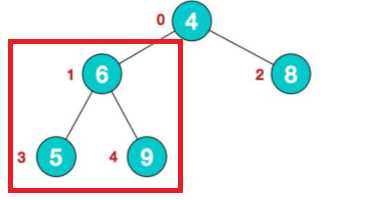
现在只需要关注红框的子树。

2.先把最后一个非叶子节点作为子树，进行堆排序。（比较他们的左右节点，把最大的和根节点进行交换）

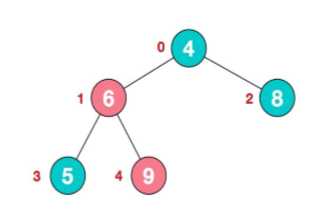
那么也就是下面已经是最大堆了。

然后在往上比较:

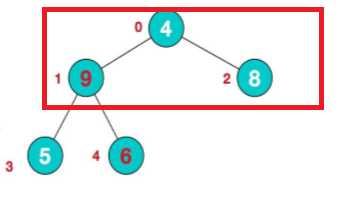
分为两种情况，一个就是加入有节点和根节点进行交换的话，那个节点就要作为子树进行堆排序。

比如这里，4和9要进行交换了，那么下面就不是最大堆了，所以左子树要再次进行最大堆结构化。

代码

static void Main(string[] args)
{
	int[] arr = { 4, 6, 8, 5, 9 };
	//制作成第一个大顶堆
	for (int i=arr.Length/2-1;i>=0;i--)
	{
		adjustHeap(arr,i,arr.Length);
	}
	int temp = 0;
	for (int j = arr.Length - 1; j > 0; j--)
	{
		//交换
		temp = arr[j];
		arr[j] = arr[0];
		arr[0] = temp;
		// j 为需要比较元素的个数为:j-1+1=j
		adjustHeap(arr, 0, j);
	}
	foreach (var i in arr)
	{
		Console.WriteLine(i);
	}
	Console.ReadKey();
}

public static void adjustHeap(int[] arr,int i,int lenght)
{
	int temp = arr[i];

	for (int k= 2*i+1;k < lenght; k=2*k+1)
	{
		if (k + 1 < lenght)
		{
			if (arr[k] < arr[k + 1])
			{
				k++;
			}
		}
		if (arr[k] > arr[i])
		{
			arr[i] = arr[k];
			i = k;
		}
		else
		{
			//因为下面都是排序好了的
			break;
		}
	}
	arr[i] = temp;
}

结果:

性能测试

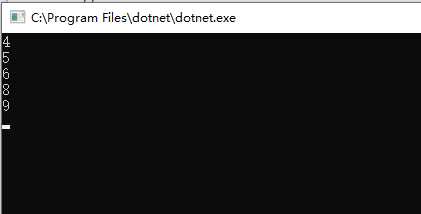
static void Main(string[] args)
{
	//int[] arr = { 4, 6, 8, 5, 9 };

	int[] arr = new int[8000000];
	for (int i = 0; i < 8000000; i++)
	{
		arr[i] = (int)((new Random().Next()) * 8000000); // 生成一个[0, 8000000) 数
	}
	Stopwatch stopwatch = new Stopwatch();
	stopwatch.Start();
	//制作成第一个大顶堆
	for (int i=arr.Length/2-1;i>=0;i--)
	{
		adjustHeap(arr,i,arr.Length);
	}
	int temp = 0;
	for (int j = arr.Length - 1; j > 0; j--)
	{
		//交换
		temp = arr[j];
		arr[j] = arr[0];
		arr[0] = temp;
		// j 为需要比较元素的个数为:j-1+1=j
		adjustHeap(arr, 0, j);
	}
	stopwatch.Stop();
	Console.WriteLine(stopwatch.ElapsedMilliseconds);
	
	Console.ReadKey();
}

public static void adjustHeap(int[] arr,int i,int lenght)
{
	int temp = arr[i];

	for (int k= 2*i+1;k < lenght; k=2*k+1)
	{
		if (k + 1 < lenght)
		{
			if (arr[k] < arr[k + 1])
			{
				k++;
			}
		}
		if (arr[k] > arr[i])
		{
			arr[i] = arr[k];
			i = k;
		}
		else
		{
			//因为下面都是排序好了的
			break;
		}
	}
	arr[i] = temp;
}

测试的时间为:

重新整理数据结构与算法(c#)—— 堆排序[二十一]

标签：数据结构   大顶堆   lang   public   制作   load   最大的   key   第一个   

原文地址：https://www.cnblogs.com/aoximin/p/13260098.html