重新整理数据结构与算法(c#)—— 二叉树排序树补删除节点[二十二]

标签：假设   null   技术   length   二叉树   最小值   add   main   正文   

前言

续前一章。

正文

删除节点规则:

1.假如删除的是叶子节点，让他的父节点，断开和它的联系。

2.如果删除节点右左子树或者右子树的话，那么应该这样。

如果删除节点是它的父节点的左节点，而删除节点有左节点，那么删除节点的父节点的左节点就等于删除节点的左节点。

举个栗子哈:

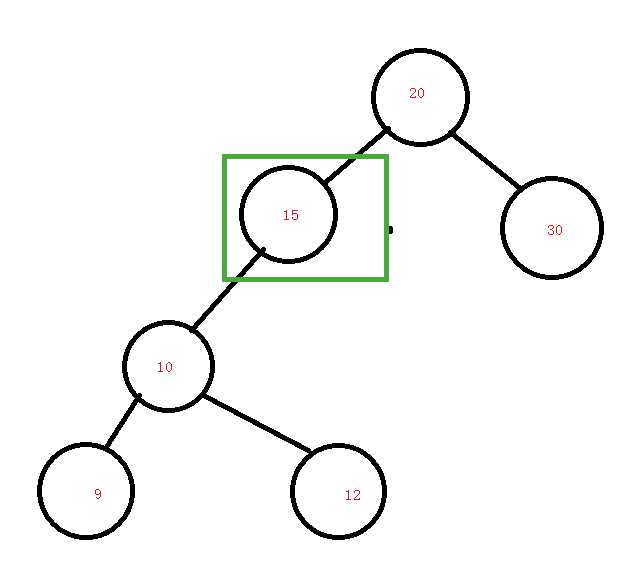
假如要删除的是15，那么20的左节点指向10。

为什么可以这样呢？其实我们的目的是什么呢？就是删除后还能保持原有的规则，20>15,就一定大于10，那么这个时候就是符合的。

如果删除节点是它的父节点的左节点，而删除节点有右节点，那么删除节点的父节点的左节点就等于删除节点的右节点。

为什么可以这样呢？

看图:

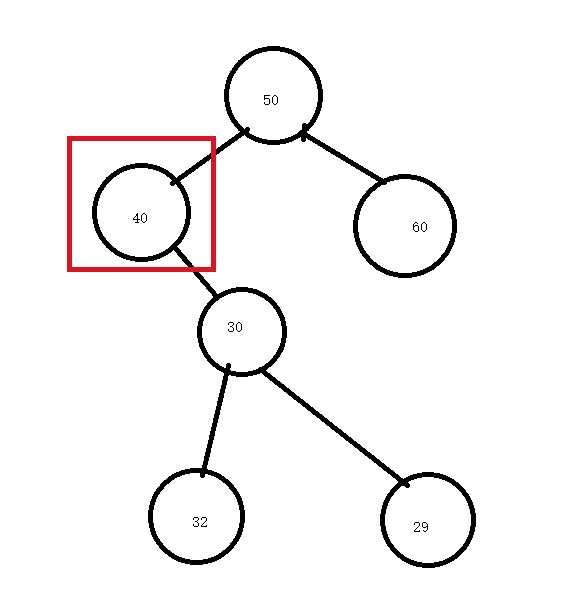
假设删除40，而40的左节点一定小于50，如果不小于是不会到左边的，这里是50>30,所以成立。

后面如果删除节点是父节点的右子树，怎么样，按照这样类推。

3.如果删除节点有左子树还有右子树。

规则是这样子的，有两种办法：
1.将删除节点的左子树最小的删除，然后删除节点的值等于左子树删除最小的那个值。
2.将删除节点右子树最大的值，然后删除节点的值等于右子树删除最大的那个值。

为什么是这样呢？可以按照上面画图就明白，以前的图丢了。

代码和测试

这里贴树模型，节点模型上一节的一样。
代码:

public class BinarySortTree
{
	//根节点
	Node root;
	public BinarySortTree(Node root)
	{
		this.root = root;
	}

	public BinarySortTree() : this(null)
	{

	}

	public void add(Node node)
	{
		if (root == null)
		{
			root = node;
		}
		else
		{
			this.root.addNode(node);
		}
	}

	public void infixOrder()
	{
		if (root == null)
		{
			Console.WriteLine("root 为空");
		}
		else
		{
			root.infixOrder();
		}
	}

	public Node searchNode(int value)
	{
		if (root==null)
		{
			Console.WriteLine("root 为空");
		}
		return root.searchNode(value);
	}

	public int delRightTreeMin(Node node)
	{
		Node tagert = node;
		while (tagert.left!=null)
		{
			tagert = tagert.left;
		}
		delNode(tagert.Value);
		return tagert.Value;
	}

	public Node searchParentNode(int value)
	{
		if (root != null)
		{
			return root.searchParentNode(value);
		}
		return null;
	}

	public void delNode(int value)
	{
		if (root == null)
		{
			return;
		}
		Node node=searchNode(value);
		if (node == null)
		{
			return;
		}
		if (node.Value == root.Value)
		{
			root = null;
			return;
		}
		Node parent = searchParentNode(value);
		if (node.left == null && node.right == null)
		{
			if (parent.left.Value == value)
			{
				parent.left = null;
			}
			else
			{
				parent.right = null;
			}
		}
		else if (node.left != null && node.right != null)
		{
			 //删除左边最大值或者右边最小值,然后修改值为删除的值
			 parent.right.Value=delRightTreeMin(node.right);
		}
		else
		{
			if (node.left != null)
			{
				if (parent.left.Value == value)
				{
					parent.left = node.left;
				}
				else
				{
					parent.right = node.left;
				}
			}
			else {
				if (parent.left.Value == value)
				{
					parent.left = node.right;
				}
				else
				{
					parent.right = node.right;
				}
			}
		}
	}
}

测试:

static void Main(string[] args)
{
	int[] arr = { 7, 3, 10, 12, 5, 1, 9, 2 };
	BinarySortTree binarySortTree = new BinarySortTree();
	//循环的添加结点到二叉排序树
	for (int i = 0; i < arr.Length; i++)
	{
		binarySortTree.add(new Node(arr[i]));
	}
	//中序遍历后的数据
	binarySortTree.infixOrder();
	binarySortTree.delNode(12);
	binarySortTree.delNode(5);
	binarySortTree.delNode(10);
	binarySortTree.delNode(2);
	binarySortTree.delNode(3);
	binarySortTree.delNode(9);
	binarySortTree.delNode(1);
	binarySortTree.delNode(7);
	Console.WriteLine("删除后的元素");
	binarySortTree.infixOrder();
	Console.Read();
}

测试结果:

重新整理数据结构与算法(c#)—— 二叉树排序树补删除节点[二十二]

标签：假设   null   技术   length   二叉树   最小值   add   main   正文   

原文地址：https://www.cnblogs.com/aoximin/p/13281844.html