标签:line info 不同 bsp omega 就是 包含 src 曲线
阿基米德螺线亦称“等速螺线”。当一点P沿动射线OP以等速率运动的同时,该射线又以等角速度绕点O旋转,点P的轨迹称为“阿基米德螺线”。
阿基米德螺线的笛卡尔坐标方程式为:
r=10*(1+t)
x=r*cos(t * 360)
y=r*sin(t *360)
编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>阿基米德螺线</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext(‘2d‘);
context.fillStyle="#EEEEFF";
context.fillRect(0,0,300,300);
context.strokeStyle="red";
context.lineWidth=2;
var dig=Math.PI/32;
context.beginPath();
context.moveTo(150,150);
for (var i=1;i<=256;i++)
{
x=150+5*i*dig*Math.sin(i*dig);
y=150+5*i*dig*Math.cos(i*dig);
context.lineTo(x,y);
}
context.stroke();
}
</script>
</head>
<body onload="draw(‘myCanvas‘);">
<canvas id="myCanvas" width="300" height="300"></canvas>
</body>
</html>
将上述HTML代码保存到一个html文本文件中,再在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出一条阿基米德螺线,如图1所示。

图1 阿基米德螺线
一个质点同时在X轴和Y轴上作简谐运动形成的图形就是李萨如曲线。
李萨如曲线上的每一个点都可以用如下的公式进行表示:
X=A1sin(ω1t+ψ1)
Y=A2sin(ω2t+ψ2)
为绘制李萨如曲线,编写如下的HTML文件。
在程序中,设定 X=R*SIN(n*θ),Y= R*SIN(k*θ) (0≤θ≤2π)
<!DOCTYPE html>
<head>
<title>李萨如曲线</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext(‘2d‘);
context.fillStyle="#EEEEFF";
context.fillRect(0,0,450,450);
context.strokeStyle="red";
context.lineWidth=1;
var dig=Math.PI/64;
context.beginPath();
n=0;
b=30;
for (py=50;py<=450;py+=70)
{
n=n+1; k=0;
for (px=50;px<=450;px+=70)
{
k++;
for (var i=0;i<=128;i++)
{
x=px+b*Math.sin(n*i*dig);
y=py-b*Math.sin(k*i*dig);
if (i==0)
{
context.moveTo(x,y);
bx=x; by=y;
}
else
context.lineTo(x,y);
}
context.lineTo(bx,by);
context.closePath();
context.fill();
context.stroke();
}
}
}
</script>
</head>
<body onload="draw(‘myCanvas‘);">
<canvas id="myCanvas" width="450" height="450"></canvas>
</body>
</html>
将上述HTML代码保存到一个html文本文件中,再在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出6种李萨如曲线,如图2所示。

图2 李萨如曲线
由图2看出,当n=1,k=1时,李萨如曲线为一条直线。如果在Y坐标计算时加上一个相位,如修改为“y=py-b*Math.sin(k*i*dig+Math.PI/4);”,则绘制的李萨如曲线如图3所示。

图3 李萨如曲线
设李萨如曲线上的点(x,y)计算式为:
X=A1sin(mθ)
Y=A2sin(nθ) (0≤θ≤2π)
我们可以设置不同的参数A1、A2、m、n,绘制出不同的李萨如曲线。
编写的HTML代码如下。
<!DOCTYPE html>
<head>
<title>可设置参数的李萨如曲线</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext(‘2d‘);
context.fillStyle="#EEEEFF";
context.fillRect(0,0,300,300);
context.strokeStyle="red";
context.lineWidth=1;
var dig=Math.PI/64;
context.beginPath();
var a1=eval(document.myForm.A1.value);
var a2=eval(document.myForm.A2.value);
var n=eval(document.myForm.N.value);
var m=eval(document.myForm.M.value);
px=150; py=150;
for (var i=0;i<=128;i++)
{
x=px+a1*Math.sin(m*i*dig);
y=py-a2*Math.sin(n*i*dig);
if (i==0)
{
context.moveTo(x,y);
bx=x; by=y;
}
else
context.lineTo(x,y);
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
}
</script>
</head>
<body>
<form name="myForm">李萨如曲线上的点(x,y)计算式为:<br>
X=A1sin(mθ) <br> Y=A2sin(nθ) (0≤θ≤2π) <br>
A1<input type=number name="A1" value=100 size=3>
A2<input type=number name="A2" value=100 size=3><br>
M <input type=number name="M" value=3 size=3>
N <input type=number name="N" value=5 size=3>
<input type=button value="确定" onClick="draw(‘myCanvas‘);">
</form><br>
<canvas id="myCanvas" width="300" height="300">
</canvas>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中,设置相应的参数后,单击“确定”按钮,可绘制出相应的李萨如曲线,如图4所示。
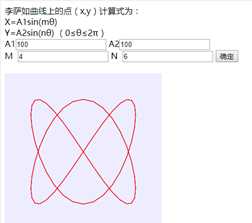
图4 李萨如曲线
在0~6π的螺线上取72个点,在这72个点的位置绘制72个李萨如曲线,并且李萨如曲线随着R值的变大而逐渐变大。编写HTML文件如下。
<!DOCTYPE html>
<head>
<title>阿基米德螺线和李萨如曲线</title>
<script type="text/javascript">
function draw(id)
{
var canvas=document.getElementById(id);
if (canvas==null)
return false;
var context=canvas.getContext(‘2d‘);
context.fillStyle="#EEEEFF";
context.fillRect(0,0,500,300);
context.strokeStyle="red";
context.lineWidth=2;
var r=0;
for (var i=0;i<6*Math.PI;i+=Math.PI/12)
{
r+=3;
px=265+(r+40)*Math.sin(i);
py=150+(r/2+25)*Math.cos(i);
var dig=Math.PI/64;
context.beginPath();
for (var j=0;j<=128;j++)
{
x=px+r/7*Math.sin(j*dig);
y=py-r/14*Math.sin(j*dig+Math.PI/5);
if (j==0)
{
context.moveTo(x,y);
bx=x; by=y;
}
else
context.lineTo(x,y);
}
context.lineTo(bx,by);
context.closePath();
context.stroke();
}
}
</script>
</head>
<body onload="draw(‘myCanvas‘);">
<canvas id="myCanvas" width="500" height="300"></canvas>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出如图5所示的由李萨如曲线构成的螺线图案。

图5 由李萨如曲线构成的螺线
标签:line info 不同 bsp omega 就是 包含 src 曲线
原文地址:https://www.cnblogs.com/cs-whut/p/13298377.html