标签：code   ++   开始   while   答案   strong   ide   sort   归并   

归并排序

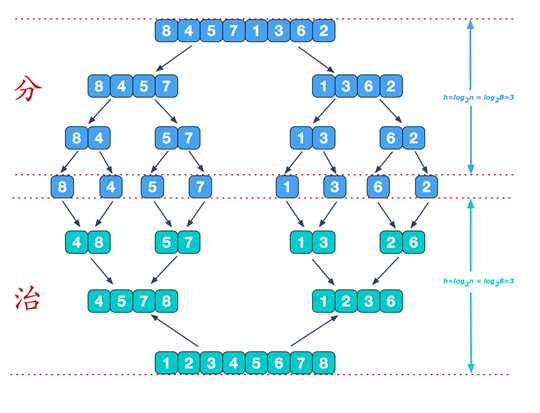
归并排序介绍:归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

 /**
     * 分解
     *
     * @param arr   数组
     * @param left  左边起点
     * @param right 右边终点
     * @param temp  转换数组
     */
    public static void mergeSort(int[] arr, int left, int right, int[] temp) {
        int mid = (left + right) / 2;
        if (left < right) {
            //左分
            mergeSort(arr, left, mid, temp);
            //右分
            mergeSort(arr, mid + 1, right, temp);
            //左右合并
            merge(arr, left, mid, right, temp);

        }
        //合并

    }

    /**
     * 合并
     *
     * @param arr   数组
     * @param left  左边开始
     * @param mid   右边开始
     * @param right 右边结束
     * @param temp  转换数组
     */

    public static void merge(int[] arr, int left, int mid, int right, int[] temp) {

        int t = 0;//临时数组开始下标
        int leftIndex=left;//左边开始下标
        int midIndex=mid+1;//右边开始下标
        while (leftIndex <= mid&&midIndex<=right) {
            //两边进行比较 小的放入临时数组
            if (arr[leftIndex] <= arr[midIndex]) {
                temp[t] = arr[leftIndex];
                t++;
                leftIndex++;
            } else {
                temp[t] = arr[midIndex];
                t++;
                midIndex++;
            }
        }
        //右边全部比较完毕左边有剩余
        while (leftIndex<=mid){
            temp[t] = arr[leftIndex];
            t++;
            leftIndex++;
        }
        //左边全部比较完毕右边有剩余
        while (midIndex<=right){
            temp[t] = arr[midIndex];
            t++;
            midIndex++;
        }

        //全部比较完毕 从临时数组放入到arr中
        t=0;
        for (int i=left;i<=right;i++){
            arr[i]=temp[t++];
        }


    }

归并排序

标签：code   ++   开始   while   答案   strong   ide   sort   归并   

原文地址：https://www.cnblogs.com/huangshen/p/13339598.html