排序算法之 '归并排序'

标签：原理图   ==   turn   包含   ali   归并   存储   pointer   顺序   

归并排序

归并排序（Merge Sort）是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

归并排序采用分而治之的原理：

• 将一个序列从中间位置分成两个序列；

• 再将这两个子序列按照第一步继续二分下去；

  • 直到所有子序列的长度都为1，也就是不可以再二分截止。这时候再两两合并成一个有序序列即可。
    • 如何合并？
      • 下图中的倒数第三行表示为第一次合并后的数据。其中一组数据为 4 8 ， 5 7。该两组数据合并方式为：每一小组数据中指定一个指针，指针指向每小组数据的第一个元素，通过指针的偏移指定数据进行有序排列。排列情况如下：
        • left_pointer指向4，right_pointer指向5，left_pointer和right_pointer指向的元素4和5进行比较，较小的数据归并到一个新的列表中。经过比较left_pointer指向的4会被添加到新的列表中，则left_pointer向后偏移一位，指向了8，right_pointer不变。
        • left_pointer和right_pointer指向的元素8，5继续比较，则right_pointer指向的5较小，添加到新列表中，right_pointer向后偏移一位，指向了7。
        • left_pointer和right_pointer指向的元素8，7继续比较，7添加到新列表中，right_pointer偏移指向NULL，比较结束。
        • 最后剩下的指针指向的数据（包含该指针指向数据后面所有的数据）直接添加到新列表中即可。

原理图示

稳定性

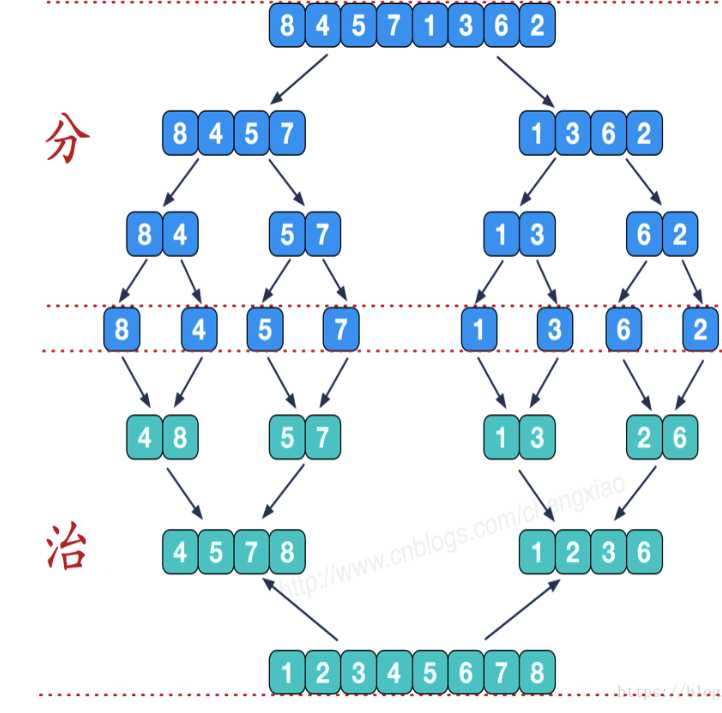
相同元素在顺序重排之后，其前后顺序不会发生变化，故归并排序是一种稳定的排序算法

Python实现

def merge_sort(alist):
    n = len(alist)
    # 结束递归的条件
    if n <= 1:
        return alist
    # 中间索引
    mid = n // 2

    left_li = merge_sort(alist[:mid])
    right_li = merge_sort(alist[mid:])

    # 指向左右表中第一个元素的指针
    left_pointer, right_pointer = 0, 0

    # 合并数据对应的列表：该表中存储的为排序后的数据
    result = []

    while left_pointer < len(left_li) and right_pointer < len(right_li):
        # 比较最小集合中的元素，将最小元素添加到result列表中
        if left_li[left_pointer] < right_li[right_pointer]:
            result.append(left_li[left_pointer])
            left_pointer += 1
        else:
            result.append(right_li[right_pointer])
            right_pointer += 1

    # 当左右表的某一个表的指针偏移到末尾的时候，比较大小结束，将另一张表中的数据（有序）添加到result中
    result += left_li[left_pointer:]
    result += right_li[right_pointer:]

    return result


if __name__ == ‘__main__‘:
    alist = [8, 4, 5, 7, 1, 3, 6, 2]
    print(merge_sort(alist))

# [1, 2, 3, 4, 5, 6, 7, 8]

排序算法之 '归并排序'

标签：原理图   ==   turn   包含   ali   归并   存储   pointer   顺序   

原文地址：https://www.cnblogs.com/fengting0913/p/13341423.html