three.js 数学方法之Vector3

时间：2020-07-22 11:21:04 阅读：360 评论：0 收藏：0 [点我收藏+]

标签：cetos nsf oar rect 地址等于 random make sla

今天郭先生来说一说three.js的Vector3，该类表示的是一个三维向量（3D vector）。一个三维向量表示的是一个有顺序的、三个为一组的数字组合（标记为x、y和z），可被用来表示很多事物，它的构造函数为Vector3( x : Float, y : Float, z : Float )x - 向量的x值，默认为0。y - 向量的y值，默认为0。z - 向量的z值，默认为0。创建一个新的Vector3。我仍然从它的属性，方法说起。

1. Vector3的属性

1. isVector3

用于测试这个类或者派生类是否为Vector3，默认为true。

2. Vector3的方法

1. set( x: number, y: number, z: number ): this

设置该向量的x、y 和 z 分量。很简单，就不说了

2. setScalar( scalar: number ): this

将该向量的x、y和z值同时设置为等于传入的scalar。也很简单。

3. setX( x: number ): Vector3;

将向量中的x值替换为x。

var vec1 = new THREE.Vector3(1,1,1);
var vec2 = new THREE.Vector3(1,2,3);
vec1.setX(2);//替换后返回新的Vector3，同时修改原Vector3

4. setY( y: number ): Vector3

将向量中的y值替换为y。同上。

5. setZ( z: number ): Vector3

将向量中的z值替换为z。同上。

6. setComponent( index: number, value: number ): this

若index为 0 则设置 x 值为 value。若index为 1 则设置 y 值为 value。若index为 2 则设置 z 值为 value。

var vec1 = new THREE.Vector3(1,1,1);
var vec2 = new THREE.Vector3(1,2,3);
vec1.setComponent(0, 2);//返回Vector3 {x: 2, y: 1, z: 1}

7. getComponent( index: number ): number

如果index值为0返回x值。如果index值为1返回y值。如果index值为2返回z值。就不多讲。

8. clone(): this

返回一个新的Vector3，其具有和当前这个向量相同的x、y和z。

var vec1 = new THREE.Vector3(1,2,3); 
var vec2 = vec1.clone()

9. copy( v: Vector3 ): this

将所传入Vector3的x、y和z属性复制给这一Vector3。

var vec1 = new THREE.Vector3(1,2,3); 
var vec2 = new THREE.Vector3().copy(vec1);

10. add( v: Vector3, w?: Vector3 ): this

将传入的向量v和这个向量相加。

var vec1 = new THREE.Vector3(1,1,1); 
var vec2 = new THREE.Vector3(1,2,3); 
vec1.add(vec2);//返回Vector3 {x: 2, y: 3, z: 4}

11. addScalar( s: number ): this

将传入的标量s和这个向量的x值、y值以及z值相加

var vec1 = new THREE.Vector3(1,2,3); 
var vec2 = vec1.addScalar(1);//返回Vector3 {x: 2, y: 3, z: 4}

12. addScaledVector( v: Vector3, s: number ): this

将所传入的v与s相乘所得的乘积和这个向量相加。

var vec1 = new THREE.Vector3(1,0,0); 
var vec2 = new THREE.Vector3(0,1,0); 
var vec3 = vec1.addScaledVector(vec2, 3);//返回Vector3 {x: 1, y: 3, z: 0}

13. addVectors( a: Vector3, b: Vector3 ): this

将该向量设置为a + b。

var vec1 = new THREE.Vector3(1,2,3); 
var vec2 = new THREE.Vector3(2,3,4); 
new THREE.Vector3().addVectors(vec1, vec2);//返回Vector3 {x: 3, y: 5, z: 7}

14. sub( a: Vector3 ): this

从该向量减去向量v。

var vec1 = new THREE.Vector3(1,2,3); 
var vec2 = new THREE.Vector3(2,3,4); 
vec2.sub(vec1);//Vector3 {x: 1, y: 1, z: 1}

14. subScalar( s: number ): this

从该向量的x、y和z中减去标量s。

var vec1 = new THREE.Vector3(1,2,3); 
var vec2 = new THREE.Vector3(2,3,4); 
var vec3 = vec2.subScalar(1);//返回Vector3 {x: 1, y: 2, z: 3}

15. subVectors( a: Vector3, b: Vector3 ): this

将该向量设置为a - b。

var vec1 = new THREE.Vector3(1,2,3); 
var vec2 = new THREE.Vector3(2,3,4); 
new THREE.Vector3().subVectors(vec2, vec1);//返回Vector3 {x: 1, y: 1, z: 1}

16. multiply( v: Vector3 ): this

将该向量与所传入的向量v进行相乘。

var vec1 = new THREE.Vector3(1,2,3); 
var vec2 = new THREE.Vector3(2,3,4); 
vec1.multiply(vec2);//返回Vector3 {x: 2, y: 6, z: 12}

17. multiplyScalar( s: number ): this

将该向量与所传入的标量s进行相乘。

var vec1 = new THREE.Vector3(1,2,3); 
vec1.multiplyScalar(2);//返回Vector3 {x: 2, y: 4, z: 6}

18. multiplyVectors( a: Vector3, b: Vector3 ): this

按照分量顺序，将该向量设置为和a * b相等。

var vec1 = new THREE.Vector3(1,2,3); 
var vec2 = new THREE.Vector3(2,3,4); 
new THREE.Vector3().multiplyVectors(vec1, vec2);//返回Vector3 {x: 2, y: 6, z: 12}

19. applyEuler( euler: Euler ): this

通过将Euler（欧拉）对象转换为Quaternion（四元数）并应用，将欧拉变换应用到这一向量上。

var vec1 = new THREE.Vector3(1,0,0); 
var euler = new THREE.Euler(0,0,Math.PI/4); 
vec1.applyEuler(euler);//返回Vector3 {x: 0.7071067811865475, y: 0.7071067811865476, z: 0}

20. applyAxisAngle( axis: Vector3, angle: number ): this

将轴和角度所指定的旋转应用到该向量上。同样是将旋转应用到Vector3上。

var vec1 = new THREE.Vector3(1,0,0); 
vec1.applyAxisAngle(new THREE.Vector3(0,0,1), Math.PI/4);//效果同上

21. applyMatrix3( m: Matrix3 ): this

将该向量乘以三阶矩阵m。

x
var vec1 = new THREE.Vector3(1,0,0); 
var matrix = new THREE.Matrix3().setFromMatrix4(new THREE.Matrix4().makeRotationZ(-Math.PI/6)); 
vec1.applyMatrix3(matrix)//返回Vector3 {x: 0.8660254037844387, y: -0.49999999999999994, z: 0}

22. applyMatrix4( m: Matrix4 ): this

将该向量乘以四阶矩阵m（第四个维度隐式地为1）

var vec1 = new THREE.Vector3(1,0,0); 
var matrix = new THREE.Matrix4().makeRotationZ(-Math.PI/6);
vec1.applyMatrix4(matrix);//返回值和上面相同

23. applyQuaternion( q: Quaternion ): this

将Quaternion变换应用到该向量。

var vec1 = new THREE.Vector3(1,0,0); 
var quaternion = new THREE.Quaternion().setFromAxisAngle(new THREE.Vector3(0,0,1), Math.PI/2) 
vec1.applyQuaternion(quaternion);//返回Vector3 {x: 0, y: 1, z: 0}

24. project( camera: Camera ): this

使用所传入的摄像机来投影（projects）该向量。

//three.js源码为 
new THREE.Vector3().applyMatrix4( camera.matrixWorldInverse ).applyMatrix4( camera.projectionMatrix );

25. unproject( camera: Camera ): this

使用所传入的摄像机来反投影（projects）该向量。

//three.js源码为 
new THREE.Vector3().applyMatrix4( camera.projectionMatrixInverse ).applyMatrix4( camera.matrixWorld );

26. transformDirection( m: Matrix4 ): this;

通过传入的矩阵（m的左上角3 x 3子矩阵）变换向量的方向，并将结果进行normalizes（归一化）。

var vec1 = new THREE.Vector3(1,1,0); 
var matrix = new THREE.Matrix4().makeRotationZ(Math.PI/4); 
vec1.transformDirection(matrix)//返回Vector3(0,1,0);

27. divide( v: Vector3 ): this

将该向量除以向量v。

var vec1 = new THREE.Vector3(2,3,4); 
var vec2 = new THREE.Vector3(3,4,5); 
vec1.divide(vec2)//向量相除就是将各个维度相除，返回Vector3 {x: 0.6666666666666666, y: 0.75, z: 0.8}

28. divideScalar( s: number ): this

将该向量除以标量s。如果传入的s = 0，则向量将被设置为( 0, 0, 0 )各个维度除以s，不多说

29. min( v: Vector3 ): this

如果该向量的x值、y值或z值大于所传入v的x值、y值或z值，则将该值替换为对应的最小值。

var vec1 = new THREE.Vector3(2,3,4); 
var vec2 = new THREE.Vector3(1,2,5); 
vec1.min(vec2)//返回各个维度的最小值Vector3 {x: 1, y: 2, z: 4}

30. max( v: Vector3 ): this

如果该向量的x值、y值或z值小于所传入v的x值、y值或z值，则将该值替换为对应的最大值。

var vec1 = new THREE.Vector3(2,3,4); 
var vec2 = new THREE.Vector3(1,2,5); 
vec1.max(vec2)//返回各个维度的最大值Vector3 {x: 2, y: 3, z: 5}

31. clamp( min: Vector3, max: Vector3 ): this

min - 在限制范围内，x值、y值和z的最小值。
max - 在限制范围内，x值、y值和z的最大值。
如果该向量的x值、y值或z值大于限制范围内最大x值、y值或z值，则该值将会被所对应的值取代。
如果该向量的x值、y值或z值小于限制范围内最小x值、y值或z值，则该值将会被所对应的值取代。
其实就是将值限制在最大值和最小值之间，这里不多说

32. clampScalar( min: number, max: number ): this

min - 分量将被限制为的最小值
max - 分量将被限制为的最大值
如果该向量的x值、y值或z值大于最大值，则它们将被最大值所取代。
如果该向量的x值、y值或z值小于最小值，则它们将被最小值所取代。
也就是将各个维度限定到最大值和最小值之间

var vec1 = new THREE.Vector3(1,3,5); 
vec1.clampScalar(2, 4);//返回Vector3 {x: 2, y: 3, z: 4}

33. clampLength( min: number, max: number ): this

min - 长度将被限制为的最小值
max - 长度将被限制为的最大值
如果向量长度大于最大值，则它将会被最大值所取代。
如果向量长度小于最小值，则它将会被最小值所取代。
这个是对长度的限制。

var vec1 = new THREE.Vector3(1,3,5); 
vec1.clampLength(10, 20);//vec1的长度明显不到10，所以长度会被拉长到最小值10，返回Vector3 {x: 1.690308509457033, y: 5.0709255283711, z: 8.451542547285165}

34. floor(): this

向量的分量向下取整为最接近的整数值。各个维度都向下取整，拿上一个返回值来说

var vec1 = new THREE.Vector3(1,3,5); 
vec1.clampLength(10, 20).floor();//返回Vector3 {x: 1, y: 5, z: 8}

35. ceil(): this

将该向量x分量、 y分量以及z分量向上取整为最接近的整数。不多说。

36. round(): this

向量中的分量四舍五入取整为最接近的整数值。也不多说。

37. roundToZero(): this

向量中的分量朝向0取整数（若分量为负数则向上取整，若为正数则向下取整）。也不多。

38. negate(): this

向量取反，即： x = -x, y = -y , z = -z。很容易理解。

39. dot( v: Vector3 ): number

计算该vector和所传入v的点积（dot product）。对应维度相乘然后求和，请回归高数课本。

40. lengthSq(): number

计算从(0, 0, 0)到(x, y, z)的欧几里得长度（Euclidean length，即直线长度）的平方。如果你正在比较向量的长度，应当比较的是长度的平方，因为它的计算效率更高一些。（毕竟少运算一步）。

41. length(): number

计算从(0, 0, 0) 到 (x, y, z)的欧几里得长度（Euclidean length，即直线长度）

42. manhattanLength(): number

计算该向量的曼哈顿长度（Manhattan length）。这个长度就是各个维度长度绝对值的和。

var vec1 = new THREE.Vector3(-1,1,2); 
vec1.manhattanLength();//返回4

43. manhattanDistanceTo( v: Vector3 ): number

计算该向量到所传入的v之间的曼哈顿距离（Manhattan distance）。就是两个向量各个维度最差，然后各个维度结果长度绝对值的和。

44. normalize(): this

将该向量转换为单位向量（unit vector），也就是说，将该向量的方向设置为和原向量相同，但是其长度（length）为1。就是将向量归一化。

45. setLength( l: number ): this

将该向量的方向设置为和原向量相同，但是长度（length）为l。

var vec1 = new THREE.Vector3(1,1,0); 
vec1.setLength(14.14);//返回Vector3 {x: 9.998489885977781, y: 9.998489885977781, z: 0}

46. lerp( v: Vector3, alpha: number ): this

在该向量与传入的向量v之间的线性插值，alpha是沿着线的距离长度。 —— alpha = 0 时表示的是当前向量，alpha = 1 时表示的是所传入的向量v。这个就比较有意思了。

var vec1 = new THREE.Vector3(1,0,0); 
var vec2 = new THREE.Vector3(0,1,0); 
vec1.lerp(vec2, 0);//返回Vector3 {x: 1, y: 0, z: 0} 
vec1.lerp(vec2, 0.5);//返回Vector3 {x: 0.5, y: 0.5, z: 0} 
vec1.lerp(vec2, 1);//返回Vector3 {x: 0, y: 1, z: 0}

47. lerpVectors( v1: Vector3, v2: Vector3, alpha: number ): this

将此向量设置为在v1和v2之间进行线性插值的向量，其中alpha为两个向量之间连线的距离长度。 —— alpha = 0 时表示的是v1，alpha = 1 时表示的是v2。

var vec1 = new THREE.Vector3(1,0,0); 
var vec2 = new THREE.Vector3(0,1,0); 
new THREE.Vector3().lerpVectors(vec1, vec2, 0); 
new THREE.Vector3().lerpVectors(vec1, vec2, 0.5); 
new THREE.Vector3().lerpVectors(vec1, vec2, 1);//结果同上

48. cross( a: Vector3, w?: Vector3 ): this

将该向量设置为它本身与传入的v的叉积（cross product），请回归高数课本

var vec1 = new THREE.Vector3(1,0,0); 
var vec2 = new THREE.Vector3(0,2,0); 
vec1.cross(vec2)//返回Vector3 {x: 0, y: 0, z: 2}

49. crossVectors( a: Vector3, b: Vector3 ): this

将该向量设置为传入的a与b的叉积（cross product）。和上面知识形式上不一样而已。

50. projectOnVector( v: Vector3 ): this

投影（Projects）该向量到另一个向量上。就是向量在向量上的投影。

var vec1 = new THREE.Vector3(2,3,0);
var vec2 = new THREE.Vector3(1,0,0);
vec1.projectOnVector(vec2);//返回Vector3 {x: 2, y: 0, z: 0}
//three.js 源代码
var denominator = v.lengthSq();
if ( denominator === 0 ) return this.set( 0, 0, 0 );
var scalar = v.dot( this ) / denominator;
return this.copy( v ).multiplyScalar( scalar );

这里解释一下源代码，如下图。

技术图片

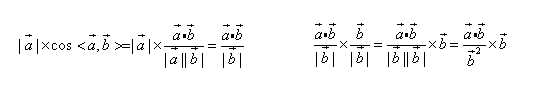
最后的结果就是vec1.copy(vec2).multiplyScalar(scalar),注意这个scalar是标量。

51 projectOnPlane( planeNormal: Vector3 ): this

将此向量投影到一个平面上，通过减去从这个向量投影得到平面法线上的向量。

var vec = new THREE.Vector3(2,2,2);
vec.projectOnPlane(new THREE.Vector3(2,0,2))//返回Vector3 {x: 0, y: 2, z: 0}
//下面是three.js源码
_vector.copy( this ).projectOnVector( planeNormal );
return this.sub( _vector );

通过源码，很容易看出，先projectOnVector得到投影，再用这个向量减去投影，得到平面法向量。（因为projectOnVector会改变原始向量，所以先copy一份）。

52. reflect( vector: Vector3 ): this

基于给定平面法线的反射线向量。法线具有单位长度。

var vec = new THREE.Vector3(1,1,0);
var res = vec.reflect(new THREE.Vector3(0,1,0));/返回Vector3 {x: 1, y: -1, z: 0}
//three.js 源码
this.sub( _vector.copy( normal ).multiplyScalar( 2 * this.dot( normal ) ) );

其实很简单，我们的入射向量为vec,反射向量设置为res,法向量设置成n,入射向量向法向量的透明为np,于是有
vec - np = np + res;
res = vec - 2 * np;
就像源码一样

53. angleTo( v: Vector3 ): number

以弧度返回该向量与向量v之间的角度。

var vec1 = new THREE.Vector3(1,1,0); 
var vec2 = new THREE.Vector3(0,1,0); 
vec1.angleTo(vec2);//返回0.7853981633974484正好是Math.PI/4的值

54. distanceTo( v: Vector3 ): number

计算该向量到所传入的v间的距离。向量平方和再开方就好，不多说。

55. distanceToSquared( v: Vector3 ): number

计算该向量到传入的v的平方距离。如果你只是将该距离和另一个距离进行比较，则应当比较的是距离的平方，因为它的计算效率会更高一些。不多说。

56. setFromSpherical( s: Spherical ): this

从球坐标s中设置该向量。球坐标系(r，θ，baiφ)与直角坐标系(x，y，z)的转换关系du：x=rsinθcosφ；y=rsinθsinφ；z=rcosθ。

var vec1 = new THREE.Vector3(); 
var spherical = new THREE.Spherical(4, Math.PI/4, Math.PI/4); 
vec1.setFromSpherical(spherical);//返回Vector3 {x: 1.9999999999999996, y: 2.8284271247461903, z: 2}

57. setFromSphericalCoords( r: number, phi: number, theta:number ): this

从球坐标中的radius、phi和theta设置该向量。和上面的方法很像，在没有现成的球坐标时，更方便。

58. setFromCylindrical( s: Cylindrical ): this

从圆柱坐标中的radius、theta和y设置该向量。

var vec1 = new THREE.Vector3(1,1,0); 
var cylindrical = new THREE.Cylindrical (4, Math.PI/4, 4); 
vec1.setFromCylindrical(cylindrical)//返回Vector3 {x: 2.82842712474619, y: 4, z: 2.8284271247461903}

59. setFromCylindricalCoords( radius: number, theta: number, y: number ): this

从圆柱坐标中的radius、theta和y设置该向量。在没有现成的圆柱坐标时，更方便。

60. setFromMatrixPosition( m: Matrix4 ): this

从变换矩阵（transformation matrix）m中，设置该向量为其中与位置相关的元素。

var vec1 = new THREE.Vector3(); 
var matrix = new THREE.Matrix4().makeTranslation(1,2,3); 
vec1.setFromMatrixPosition(matrix);//返回Vector3 {x: 1, y: 2, z: 3}

61. setFromMatrixScale( m: Matrix4 ): this

从变换矩阵（transformation matrix）m中，设置该向量为其中与缩放相关的元素。

var vec1 = new THREE.Vector3(); 
var matrix = new THREE.Matrix4().makeScale(1,2,3); 
vec1.setFromMatrixScale(matrix);//返回Vector3 {x: 1, y: 2, z: 3}

62. setFromMatrixColumn( matrix: Matrix4, index: number ): this

从传入的四阶矩阵matrix由index指定的列中，设置该向量的x值、y值和z值。

var vec1 = new THREE.Vector3(); 
var matrix = new THREE.Matrix4().set( 1,2,3,4, 2,3,4,5, 3,4,5,6, 4,5,6,7 ); 
vec1.setFromMatrixColumn(matrix, 2);//返回Vector3 {x: 3, y: 4, z: 5}，因为是第三列

63. setFromMatrix3Column( matrix: Matrix3, index: number ): this

从传入的三阶矩阵matrix由index指定的列中，设置该向量的x值、y值和z值。

var vec1 = new THREE.Vector3(); 
var matrix = new THREE.Matrix3().set( 1,2,3, 2,3,4, 3,4,5, ) 
vec1.setFromMatrixColumn(matrix, 2);//返回Vector3 {x: 3, y: 4, z: 5}

64. equals( v: Vector3 ): boolean

检查该向量和v的严格相等性。不必多说。

65. fromArray( array: number[], offset?: number ): this

设置向量中的x值为array[ offset + 0 ]，y值为array[ offset + 1 ]， z值为array[ offset + 2 ]。

var vec1 = new THREE.Vector3(); 
var array = [0,1,2,3,4,5,6,7]; 
vec1.fromArray(array, 0);//返回Vector3 {x: 0, y: 1, z: 2} vec1.fromArray(array, 2);//返回Vector3 {x: 2, y: 3, z: 4}

66. toArray( array?: number[], offset?: number ): number[]

返回一个数组[x, y ,z]，或者将x、y和z复制到所传入的array中。

var vec1 = new THREE.Vector3(1,1,2); 
vec1.toArray();//返回)[1, 1, 2]

67. random(): this

对向量的各个维度赋随机值[0,1];

var vec1 = new THREE.Vector3(); 
vec1.random()//Vector3 {x: 0.7630145272644331, y: 0.10239339520268054, z: 0.3732101353384689}

嗯，Vector3方方面面的确实挺多，大家还是要多应用。

转载请注明地址：郭先生的博客

three.js 数学方法之Vector3

标签：cetos nsf oar rect 地址等于 random make sla

原文地址：https://www.cnblogs.com/vadim-web/p/13359036.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行