标签:占用 插入排序 mamicode idt 列表 存储空间 基数排序 loading 存储
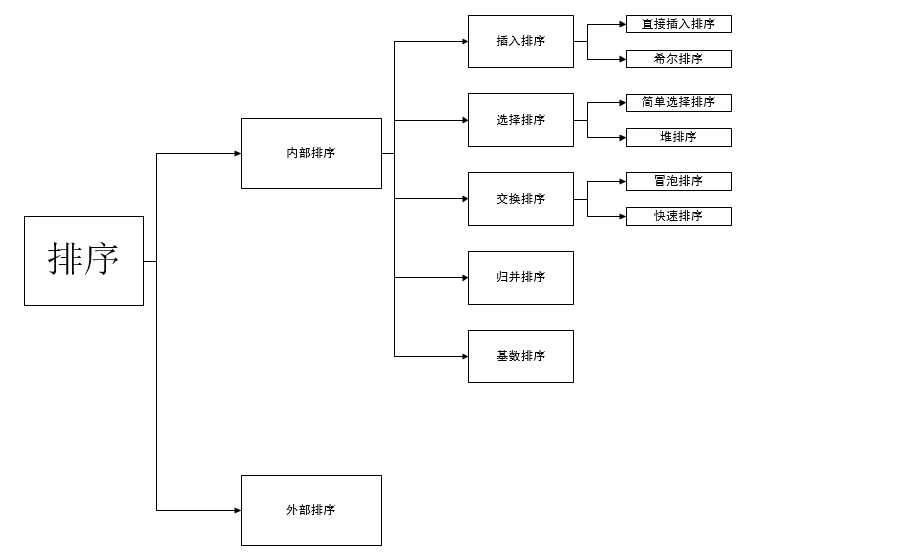
一 排序算法的分类
二 时间复杂度和空间复杂度
1.时间复杂度
1.1 时间复杂度的计算方式
1).用常数1代替运行时间中所有的加法常数
2)修改后的运行次数函数中,只保留最高阶项
3)去除最高阶项的系数
1.2 常用算法的时间复杂度
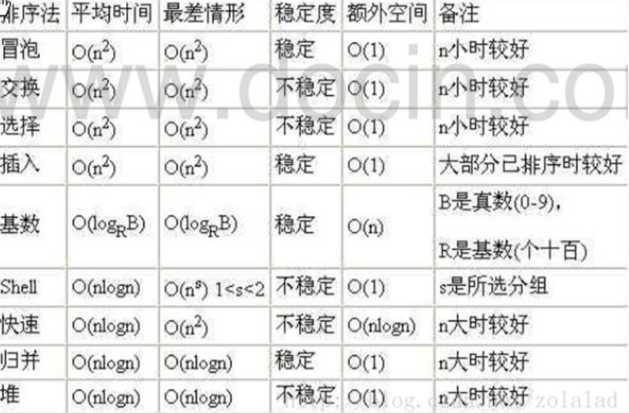
这个需要牢记
2.空间复杂度
空间复杂度是一个算法在运行时临时占用存储空间大小的量度。
例如快排、归并排序、基数排序都属于拿空间换时间的典型。
三 插入排序
3.1 直接插入排序
字面意思,例如有数组 int[] arr = {1,8,2,45,7,5,9};需要从小到大进行排序
从arr[1]开始,首先需要定义一个变量temp用于存储arr[1]的数值,8大于1,不动,将arr[1]的值赋给arr[1],此循环结束,
然后是arr[2],temp=2,2小于8,将8的数值赋给arr[2],此时是 {1,8,8,45,7,5,9},再往前比较,2<1,循环停止,将temp的值给arr[1],
依次进行。
下面是代码。

3.2 希尔排序
希尔排序是对直接插入排序的改进,最基本的理念在于,直接插入排序中,如果需要前移的次数太多,就会对效率产生很大的影响,那么通过对原数组规律得分块,再对每个块进行插入排序,就会快很多。
简而言之,底层还是插入排序,只不过在上面加了一层gap的循环。
实质上还是在该数组里进行排序,理解了插入排序之后就不难理解了。
代码

四 选择排序
4.1 简单选择排序
基本思想是:第一次从 arr[0]~arr[n-1]中选取最小值, 与 arr[0]交换,第二次从arr[1]~arr[n-1]中选取最小值,与arr[1]交换,第三次从arr[2]~arr[n-1]中选取最小值,与 arr[2] 交换,…,第 i 次从arr[i-1]~arr[n-1]中选取最小值,与arr[i-1]交换,…, 第 n-1 次从arr[n-2]~arr[n-1]中选取最小值,与 arr[n-2]交换,总共通过 n-1 次,得到一个按排序码从小到大排列的有序序列。
代码如下

4.2 堆排序
堆排序,对我而言最大的特点就是 它是二叉树,我总结了一下网上的结论,堆排序本质上也是个数组,对于一个节点 i,它的父节点为 (i-1)/2,两个子节点为2*i+1 和 2*i+2,对此,只要给定待排序的数组,就可以通过过的一个堆排序,如下代码

其中的swap方法就是交换两个节点的数值,代码如下

但堆排序获得的数组并不是一个从大到小的有序数组,所以需要下一步,也就是取堆排序的第一个数(最大值或者最小值),然后对剩下的再做一次堆排序,再取第一个数,循环往复,如下


这一部分的代码参照 https://blog.csdn.net/u010452388/article/details/81283998
五 交换排序
5.1 简单交换排序/冒泡排序
通过一个大循环和一个小循环,每次小循环会冒泡出一个当前循环列表里的最大值或者最小值
代码如下

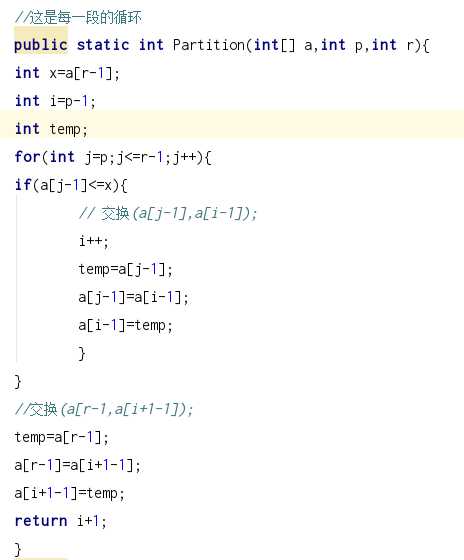
5.2 快速排序
参照https://blog.csdn.net/MoreWindows/article/details/6684558
该方法的基本思想是:
1.先从数列中取出一个数作为基准数。
2.分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
3.再对左右区间重复第二步,直到各区间只有一个数。

六 归并排序 和 基数排序
归并排序 :是利用归并的思想(将问题分解为一些小问题然后递归求解)实现的排序方法
基数排序:将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。 这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
标签:占用 插入排序 mamicode idt 列表 存储空间 基数排序 loading 存储
原文地址:https://www.cnblogs.com/chenlun127/p/13377434.html