标签：数组实现 hellip def 二维线段树 lin 下标 启示 转移 小白
今天气闷，过来写一篇小结。
内容上主要包括noip提高组常考的线段树与树状数组，还有一些拓展的算法qwq窝太蒻了。
一. 线段树
Q1：什么是线段树？
A1：线段树就是线段的树 维护区间信息（大多数是可以合并的）的树就是线段树qwq
所以线段树的每一个节点就必须要代表一个区间的信息啦。线段树的实现方法多种多样，有下传参数的数组版本和结构体实现的不带参版本，蒟蒻我觉得下传带参的版本比较无脑好写，但是结构体版本在面对动态开点等较为进阶的线段树算法时适应性更强一些。所以两个写法都要会了qwq /dz。
#include <bits/stdc++.h> using namespace std; const int N=1e5+7; typedef long long ll; inline ll read() { ll num=0ll; char ch=getchar(); while(!isdigit(ch)) ch=getchar(); while(isdigit(ch)) num=(num<<3)+(num<<1)+(ch^48), ch=getchar(); return num; } ll a[N]; struct s { int l,r; ll sum,tag; } t[N<<2]; #define ls (p<<1) #define rs (p<<1|1) #define mid ((l+r)>>1) #define Mid ((t[p].l+t[p].r)>>1) inline void pushup(int p) { t[p].sum=t[ls].sum+t[rs].sum; } inline void build(int p,int l,int r) { t[p].l=l; t[p].r=r; if(t[p].l==t[p].r) { t[p].sum=a[l]; return ; } build(ls,l,mid); build(rs,mid+1,r); pushup(p); } inline void f(int p,ll k) { t[p].sum+=k*(t[p].r-t[p].l+1); t[p].tag+=k; } inline void pushdown(int p) { f(ls,t[p].tag); f(rs,t[p].tag); t[p].tag=0ll; } inline void update(int nl,int nr,int p,ll k) { if(nl<=t[p].l && t[p].r<=nr) { f(p,k); return ; } pushdown(p); if(nl<=Mid) update(nl,nr,ls,k); if(nr>Mid) update(nl,nr,rs,k); pushup(p); } inline ll query(int ql,int qr,int p) { if(ql<=t[p].l && t[p].r<=qr) return t[p].sum; ll ans=0ll; pushdown(p); if(ql<=Mid) ans+=query(ql,qr,ls); if(qr>Mid) ans+=query(ql,qr,rs); return ans; } int main() { return 0; }
#include <bits/stdc++.h> using namespace std; const int N=1e5+7; typedef long long ll; inline ll read() { ll num=0ll; char ch=getchar(); while(!isdigit(ch)) ch=getchar(); while(isdigit(ch)) num=(num<<3)+(num<<1)+(ch^48), ch=getchar(); return num; } ll a[N]; struct s { int l,r; ll sum,tag; } t[N<<2]; #define ls (p<<1) #define rs (p<<1|1) #define mid ((l+r)>>1) #define Mid ((t[p].l+t[p].r)>>1) inline void pushup(int p) { t[p].sum=t[ls].sum+t[rs].sum; } inline void build(int p,int l,int r) { t[p].l=l; t[p].r=r; if(t[p].l==t[p].r) { t[p].sum=a[l]; return ; } build(ls,l,mid); build(rs,mid+1,r); pushup(p); } inline void f(int p,ll k) { t[p].sum+=k*(t[p].r-t[p].l+1); t[p].tag+=k; } inline void pushdown(int p) { f(ls,t[p].tag); f(rs,t[p].tag); t[p].tag=0ll; } inline void update(int nl,int nr,int p,ll k) { if(nl<=t[p].l && t[p].r<=nr) { f(p,k); return ; } pushdown(p); if(nl<=Mid) update(nl,nr,ls,k); if(nr>Mid) update(nl,nr,rs,k); pushup(p); } inline ll query(int ql,int qr,int p) { if(ql<=t[p].l && t[p].r<=qr) return t[p].sum; ll ans=0ll; pushdown(p); if(ql<=Mid) ans+=query(ql,qr,ls); if(qr>Mid) ans+=query(ql,qr,rs); return ans; } int main() { return 0; }
线段树是一种二叉树，它的左儿子（lson,ls)与右儿子(rson,rs)分别维护区间 [l,mid] 与区间 [mid+1,r] 的信息，（其中mid=(l+r)/2)，所以线段树是一种递归定义的数据结构，它的函数实现大多也都是递归的。线段树的核心思想是分治，它所维护的信息必须满足合并性质，即左子树的信息+右子树的信息=根的信息（+是合并的意思），否则很难用线段树来做。线段树几乎是一颗满二叉树，这个地方说它不是满的是因为在最底层的那一排节点会出现空缺的情况（例如[1,3]，这个时候ls就是[1,2]，而右儿子是[3,3]）。在所有根节点下标为左右儿子的一半的线段树里，线段树的下标小于N*4。线段树的所有常规操作皆为 log n 级别。（即1e5~1e6）
Q2：那么线段树具体能维护什么样子的信息呢？
A2：这个需要看具体的题目了awa。
1.首先是无脑区间操作：
这个地方我们要强调突出的是线段树的pushup（节点信息合并）与pushdown（懒标记下传）操作。为了维护某一信息，我们可能需要维护额外的信息ABCDEFGHI……（好毒瘤），这个时候就需要我们对左右区间子信息的合并方式、合并顺序进行处理，而在pushdown的时候，我们甚至在考虑方式顺序的同时，还要思考各个标记的冲突问题（QAQ），比如这道题
从最简单的题目开始罢。线段树2要求我们维护一个资磁区间加区间乘并且可以求区间和的线段树。思考区间乘法：首先我们肯定需要给它维护一个懒标记，pushdown该如何处理呢？这个时候我们可以先下传乘法，再下传加法，即若某个儿子的区间和为A，下传后我们可以将其改为（A）* tag_mul + tag_add。顺序确定了，我们再思考懒标记的更新方式。若是更新加法标记（区间加法更新）， 将这个区间都加上delta，那么其儿子的值就应当为（A）* tag_mul + tag_add + delta, 观察这个柿子我们发现加法标记可以和delta合并（即： tag_add ‘ == tag_add + delta），所以区间加的更新直接加到加法标记上即可。那么更新乘法标记（区间乘法的更新）呢？ 若将这个区间都乘上delta，那么其儿子的值就应当为（（A） * tag_mul + tag_add）* delta， 展开发现 A ‘ == A * tag_mul * delta + tag_add * delta，所以我们直接将加法标记*=delta，乘法标记+=delta即可。于是这道题就切掉了/dz。
至于为什么不先下传加法再下传乘法，手玩柿子可以发现区间加的时候更新加法标记需要先除以tag_mul再进入，这就涉及到了浮点数的运算并且带来了掉精度等一系列问题，这是不符合我们线段树清新简明的维护风格的（（（，所以不这么写。
代码如下：快读真丑
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int read();
inline ll readl();
const int N=1e5+7;
ll a[N],sum[N<<2],tag_s[N<<2],tag_m[N<<2];
ll mod;
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define mid ((l+r)>>1)
inline void pushup(int p) {
sum[p]=(sum[ls(p)]+sum[rs(p)])%mod;
}
inline void build(int p,int l,int r) {
tag_s[p]=0ll;
tag_m[p]=1ll;
if(l==r) {
sum[p]=a[l]%mod;
return ;
}
build(ls(p),l,mid);
build(rs(p),mid+1,r);
pushup(p);
}
inline void pushdown(int p,int l,int r) {
sum[ls(p)]=(sum[ls(p)]*tag_m[p]%mod+(mid-l+1)*tag_s[p]%mod)%mod;
sum[rs(p)]=(sum[rs(p)]*tag_m[p]%mod+(r-mid)*tag_s[p]%mod)%mod;
tag_s[ls(p)]=(tag_s[ls(p)]*tag_m[p]%mod+tag_s[p])%mod;
tag_s[rs(p)]=(tag_s[rs(p)]*tag_m[p]%mod+tag_s[p])%mod;
tag_m[ls(p)]=tag_m[ls(p)]*tag_m[p]%mod;
tag_m[rs(p)]=tag_m[rs(p)]*tag_m[p]%mod;
if(!tag_m[ls(p)]) tag_m[ls(p)]=mod;
if(!tag_m[ls(p)]) tag_m[ls(p)]=mod;
tag_s[p]=0ll;
tag_m[p]=1ll;
pushup(p);
}
inline void update_s(int nl,int nr,int p,int l,int r,ll k_s) {
if(nl<=l&&r<=nr) {
tag_s[p]=(tag_s[p]+k_s)%mod;
sum[p]=(sum[p]+(r-l+1)*k_s%mod)%mod;
return ;
}
pushdown(p,l,r);
if(nl<=mid) update_s(nl,nr,ls(p),l,mid,k_s);
if(nr>mid) update_s(nl,nr,rs(p),mid+1,r,k_s);
pushup(p);
}
inline void update_m(int nl,int nr,int p,int l,int r,ll k_m) {
if(nl<=l&&r<=nr) {
tag_s[p]=(tag_s[p]*k_m)%mod;
tag_m[p]=(tag_m[p]*k_m)%mod;
sum[p]=(sum[p]*k_m)%mod;
return ;
}
pushdown(p,l,r);
if(nl<=mid) update_m(nl,nr,ls(p),l,mid,k_m);
if(nr>mid) update_m(nl,nr,rs(p),mid+1,r,k_m);
pushup(p);
}
inline ll query(int ql,int qr,int p,int l,int r) {
if(ql<=l&&r<=qr) return sum[p]%mod;
ll num=0ll;
pushdown(p,l,r);
if(ql<=mid) num+=query(ql,qr,ls(p),l,mid)%mod,num%=mod;
if(qr>mid) num+=query(ql,qr,rs(p),mid+1,r)%mod,num%=mod;
return num%mod;
}
int main() {
int n,m;
n=read(); m=read();
mod=readl();
for(int i=1;i<=N-1;i++) tag_m[i]=1ll;
for(int i=1;i<=n;i++) a[i]=readl();
build(1,1,n);
while(m--) {
int t=read(),x=read(),y=read();
if(t==1) update_m(x,y,1,1,n,readl());
if(t==2) update_s(x,y,1,1,n,readl());
if(t==3) printf("%lld\n",query(x,y,1,1,n));
}
return 0;
}
inline ll readl() {
ll num=0ll; char ch=getchar();
while(ch<‘0‘||ch>‘9‘) ch=getchar();
while(ch>=‘0‘&&ch<=‘9‘)
num=(num<<3)+(num<<1)+(ll)(ch^48),
ch=getchar();
return num;
}
inline int read() {
int num=0; char ch=getchar();
while(ch<‘0‘||ch>‘9‘) ch=getchar();
while(ch>=‘0‘&&ch<=‘9‘)
num=(num<<3)+(num<<1)+(ch^48),
ch=getchar();
return num;
}
而后是这道题，洛谷P6327 区间加区间sin和，要求维护一个资磁区间加而后维护区间sin和的数据结构。 使用和角公式：（假装有公式），知道我们阔以维护区间的cos和与sin和，pushup无脑加即可。注意应当先更新sin后cos。代码：
#include <bits/stdc++.h>
using namespace std;
inline int read() {
int num=0; char ch=getchar();
while(!isdigit(ch)) ch=getchar();
while(isdigit(ch)) num=(num<<3)+(num<<1)+(ch^48), ch=getchar();
return num;
}
int n,m;
typedef double db;
const int N=2e5+7;
db Sin[N<<2],Cos[N<<2],tag[N<<2],a[N];
#define ls(p) ((p)<<1)
#define rs(p) ((p)<<1|1)
#define mid ((l+r)>>1)
inline double sumS(double sinx,double cosx,double siny,double cosy) {
return sinx*cosy + cosx*siny;
}
inline double sumC(double sinx,double cosx,double siny,double cosy) {
return cosx*cosy - sinx*siny;
}
inline void pushup(int p,int l,int r) {
Sin[p]=Sin[ls(p)]+Sin[rs(p)]; Cos[p]=Cos[ls(p)]+Cos[rs(p)];
}
inline void build(int p,int l,int r) {
if(l==r) { Sin[p]=sin(a[l]); Cos[p]=cos(a[l]); return ; }
build(ls(p),l,mid); build(rs(p),mid+1,r);
pushup(p,l,r);
}
inline void f(int p,int l,int r,double k) {
double nsin,ncos;
nsin=sumS(Sin[p],Cos[p],sin(k),cos(k));
ncos=sumC(Sin[p],Cos[p],sin(k),cos(k));
Sin[p]=nsin; Cos[p]=ncos; tag[p]+=k;
}
inline void pushdown(int p,int l,int r) {
f(ls(p),l,mid,tag[p]); f(rs(p),mid+1,r,tag[p]); tag[p]=0.0;
}
inline void update(int nl,int nr,int p,int l,int r,double k) {
if(nl<=l && r<=nr) { f(p,l,r,k); return ; }
pushdown(p,l,r);
if(nl<=mid) update(nl,nr,ls(p),l,mid,k);
if(nr>mid) update(nl,nr,rs(p),mid+1,r,k);
pushup(p,l,r);
}
inline double query(int ql,int qr,int p,int l,int r) {
if(ql<=l && r<=qr) { return Sin[p]; }
double ans=0.0;
pushdown(p,l,r);
if(ql<=mid) ans+=query(ql,qr,ls(p),l,mid);
if(qr>mid) ans+=query(ql,qr,rs(p),mid+1,r);
return ans;
}
int main() {
n=read();
for(int i=1;i<=n;i++) a[i]=(double )read();
build(1,1,n);
m=read();
for(int i=1;i<=m;i++) {
int x=read(),l=read(),r=read(),v;
if(x==1) v=read(), update(l,r,1,1,n,(double )v);
else printf("%.1f\n",query(l,r,1,1,n));
}
return 0;
}
还有这道题，洛谷P1471 方差 ，将区间平方的柿子展开发现我们需要维护区间的和，所以直接写就行了（这题为什么蓝啊喂）。笔者在写这道题时本来采用了维护区间平均数的方法，结果码量与精度直接把我当场整自闭，看了题解才知道（QAQ窝好菜）。这启示我们在用线段树处理信息时应当先思考思考，看看还有没有更简便的方法来维护ans（可能只有我这样的菜鸡才会这么做罢QAQ）。上代码：
#include <bits/stdc++.h> using namespace std; inline int read() { int num=0; char ch=getchar(); while(!isdigit(ch)) ch=getchar(); while(isdigit(ch)) num=(num<<3)+(num<<1)+(ch^48), ch=getchar(); return num; } typedef double db; const int N=1e5+7; db a[N],sum[N<<2],squ[N<<2],tag[N<<2]; int n,m; #define ls (p<<1) #define rs (p<<1|1) #define mid ((l+r)>>1) inline void pushup(int p,int l,int r) { sum[p]=sum[ls]+sum[rs]; squ[p]=squ[ls]+squ[rs]; } inline void build(int p,int l,int r) { if(l==r) { sum[p]=a[l]; squ[p]=a[l]*a[l]; return ; } build(ls,l,mid); build(rs,mid+1,r); pushup(p,l,r); } inline void f(int p,int l,int r,db k) { squ[p]+=(db)(r-l+1)*k*k+2*sum[p]*k; sum[p]+=(db)(r-l+1)*k; tag[p]+=k; } inline void pushdown(int p,int l,int r) { f(ls,l,mid,tag[p]); f(rs,mid+1,r,tag[p]); tag[p]=0.0000; } inline void update(int nl,int nr,int p,int l,int r,db k) { if(nl<=l && r<=nr) { f(p,l,r,k); return ; } pushdown(p,l,r); if(nl<=mid) update(nl,nr,ls,l,mid,k); if(nr>mid) update(nl,nr,rs,mid+1,r,k); pushup(p,l,r); } inline db query_sum(int ql,int qr,int p,int l,int r) { if(ql<=l && r<=qr) { return sum[p]; } db ans=0.0000; pushdown(p,l,r); if(ql<=mid) ans+=query_sum(ql,qr,ls,l,mid); if(qr>mid) ans+=query_sum(ql,qr,rs,mid+1,r); return ans; } inline db query_squ(int ql,int qr,int p,int l,int r) { if(ql<=l && r<=qr) { return squ[p]; } db ans=0.0000; pushdown(p,l,r); if(ql<=mid) ans+=query_squ(ql,qr,ls,l,mid); if(qr>mid) ans+=query_squ(ql,qr,rs,mid+1,r); return ans; } inline db query_ave(int l,int r) { db ans=query_sum(l,r,1,1,n); return ans/((db)r-l+1); } inline db query_squ_sum(int l,int r) { db ans=query_squ(l,r,1,1,n),ave=query_ave(l,r); db Sum=query_sum(l,r,1,1,n),len=r-l+1; // printf("%.4lf %.4lf %.4lf %.4lf\n",ans,ave,Sum,len); return (ans/len + ave*ave - 2*ave*Sum/len); } int main() { n=read(); m=read(); for(int i=1;i<=n;i++) scanf("%lf",&a[i]); build(1,1,n); for(int i=1;i<=m;i++) { int op=read(),l=read(),r=read(); if(op==1) { db k; scanf("%lf",&k); update(l,r,1,1,n,k); } if(op==2) { printf("%.4lf\n",query_ave(l,r)); } if(op==3) { printf("%.4lf\n",query_squ_sum(l,r)); } } return 0; } /* 5 2 3 1 2 5 4 2 3 3 3 3 5 */
这个题目（SP2713 GSS4 - Can you answer these queries IV ）要实现一个奇怪的区间开根操作。初看此题：区间开根是什么玄学操作？？？但是分析1下就会发现一个数字它被开根的次数是有限的。这启示我们在开根时直接暴力修改即可，使用线段树来维护一个区间是否要修改。将询问或修改常数化是我们经常使用的技巧。talk is cheap，show me the code：
#include <bits/stdc++.h> using namespace std; const int N=1e5+7; long long a[N]; typedef long long ll; int n,m; namespace tree1 { bool sum[N<<2]; ll S[N<<2]; #define ls (p<<1) #define rs (p<<1|1) #define mid ((l+r)>>1) inline void pushup(int p) { sum[p]=(sum[ls] && sum[rs]); S[p]=S[ls]+S[rs]; } inline void build(int p,int l,int r) { if(l==r) { sum[p]=(a[l]==1ll||a[l]==0ll ? true : false ); S[p]=a[l]; return ; } build(ls,l,mid); build(rs,mid+1,r); pushup(p); } inline void update(int ql,int qr,int p,int l,int r) { if(l==r) { S[p]=sqrt(S[p]); if(S[p]==1ll) sum[p]|=true ; return ; } if(ql<=mid && (!sum[ls])) update(ql,qr,ls,l,mid); if(qr>mid && (!sum[rs])) update(ql,qr,rs,mid+1,r); pushup(p); } inline ll query(int ql,int qr,int p,int l,int r) { if(ql<=l && r<=qr) return S[p]; ll ans=0ll; if(ql<=mid) ans+=query(ql,qr,ls,l,mid); if(qr>mid) ans+=query(ql,qr,rs,mid+1,r); return ans; } } using namespace tree1; int solve() { memset(a,0,sizeof(a)); memset(S,0,sizeof(S)); memset(sum,0,sizeof(sum)); for(int i=1;i<=n;i++) scanf("%lld",&a[i]); build(1,1,n); scanf("%d",&m); for(int i=1;i<=m;i++) { int op,l,r; scanf("%d%d%d",&op,&l,&r); if(r<l) swap(l,r); if(op==0) update(l,r,1,1,n); if(op==1) printf("%lld\n",query(l,r,1,1,n)); } return 0; } int main() { int T=0; while(scanf("%d",&n)!=EOF) { printf("Case #%d:\n",++T); solve(); printf("\n"); } return 0; }
通过以上几道题，我们发现线段树在维护区间的数学问题时大都需要序列满足一种像分配律一样的性质（可以将一个序列的和/积等对一个数进行操作），这就初步体现了线段树的区间合并思想。下面的题目就脱离了数学的约束，渐渐玄学/youl
洛谷P4513 公园逛小白，这需要我们维护一个可以单点修改区间求最大子段和的东西。这里有一个做线段树的题目的思想：如果ls rs的信息都已经求好了，那么我应该怎么把他们合并在一起？如果我要合并他们，我还需要什么信息来辅助我合并？如果我的信息都已经处理好了，upd的时候该如何更新它们？把这些问题想好了，题目就做出来了。看这个题目，单点修改 ≌ 不用写懒标记 ≌ 可以少想很多事情，所以pushdown就不需要了。思考：一个序列的最大子段和与ls rs有什么关系？有可能全在左子区间，有可能全在右子区间，有可能一部分在左子区间一部分在右子区间。对于第一二种情况，固然将左右子树的ans无脑求max转移到根即可。对于第三种情况呢？显然左子树从右边开始的最大子段和加上右子树从左边开始的最大子段和等于一部分在左子区间一部分在右子区间的最大子段和（保证端点在左 || 右是为了保证子序列的连续性）。维护每个序列从左开始的最大子段和、从右开始的最大子段和与本序列的最大子段和即可。程序实现时应注意pushup操作的完成方式。
tip：当我们需要多个信息来维护ans时，程序的复杂之处就还会体现在query函数上。query函数在查询左右区间的ans时往往还需要返回一些另外的参数来帮助区间合并（如本题的左右子序列），这时query函数的返回值往往会开成一个与线段树节点相同的类，返回时 ls 与 rs 的合并处理方式与pushup相同。这类数据还有一种比较优秀的处理方式，就是在编写pushup之前先写好一个merge函数，这个函数有两个参数（二维线段树去死吧），参数代表线段树上级别相同的两个节点，merge可以合并这两个节点的信息并返回一个合并好的值（即这两个节点的父节点）。酱紫的话pushup与query就会好写得一批。如果我们维护的信息比较复杂，我们经常还会面临信息不可以无脑与null合并的问题。比方说一个节点只有左子树在查询区间而右子树不需要查询，这个时候我们query再返回merge（左，右）就会出大问题。就像这道题P4247 [清华集训2012]序列操作，你这一合并全乘上零这不求了个寂寞吗？所以我们就需要另外一种query写法，即判断左右子树是否需要发生递归（有没有 || 在不在查询区间），如果只有ls需要那么就直接返回ls（rs同理），若两个都有再返回merge（左，右）。下面是小园逛公白的代码。还有这道题的升级版本（SP2916 GSS5 - Can you answer these queries V）。
#include <bits/stdc++.h> using namespace std; const int INF=1000000; const int N=5e5+7; int a[N],sum[N<<2],Lsum[N<<2],Rsum[N<<2],Ssum[N<<2]; #define ls (p<<1) #define rs (p<<1|1) #define mid ((l+r)>>1) inline void pushup(int p,int l,int r) { Ssum[p]=Ssum[ls]+Ssum[rs]; sum[p]=max(Rsum[ls]+Lsum[rs],max(sum[ls],sum[rs])); Lsum[p]=max(Lsum[ls],Ssum[ls]+Lsum[rs]); Rsum[p]=max(Rsum[rs],Ssum[rs]+Rsum[ls]); } inline void build(int p,int l,int r) { if(l==r) { sum[p]=Lsum[p]=Rsum[p]=Ssum[p]=a[l]; return ; } build(ls,l,mid); build(rs,mid+1,r); pushup(p,l,r); } inline void update(int p,int l,int r,int pos,int k) { if(l==r) { sum[p]=Lsum[p]=Rsum[p]=Ssum[p]=k; return ; } if(pos<=mid) update(ls,l,mid,pos,k); if(pos>mid) update(rs,mid+1,r,pos,k); pushup(p,l,r); } struct s { int ans_sum,ans_Lsum,ans_Rsum,ans_Ssum; s(int a1,int a2,int a3,int a4) { this->ans_sum=a1; this->ans_Lsum=a2,this->ans_Rsum=a3; this->ans_Ssum=a4; } }; inline struct s query(int ql,int qr,int p,int l,int r) { // printf("%d %d %d %d %d %d %d %d %d\n", // ql,qr,p,l,r,sum[p],Lsum[p],Rsum[p],Ssum[p]); if(ql<=l && r<=qr) return s(sum[p],Lsum[p],Rsum[p],Ssum[p]); struct s ans=s(0,0,0,0),op1=s(-INF,-INF,-INF,-INF),op2=s(-INF,-INF,-INF,-INF); if(ql<=mid) op1=query(ql,qr,ls,l,mid); if(qr>mid) op2=query(ql,qr,rs,mid+1,r); ans.ans_sum=max(op1.ans_Rsum+op2.ans_Lsum,max(op1.ans_sum,op2.ans_sum)); ans.ans_Lsum=max(op1.ans_Lsum,op1.ans_Ssum+op2.ans_Lsum); ans.ans_Rsum=max(op2.ans_Rsum,op2.ans_Ssum+op1.ans_Rsum); ans.ans_Ssum=op1.ans_Ssum+op2.ans_Ssum; return ans; } int main() { int n,m; scanf("%d",&n); scanf("%d",&m); for(int i=1;i<=n;i++) scanf("%d",&a[i]); build(1,1,n); for(int i=1;i<=m;i++) { int op,x,y; scanf("%d%d%d",&op,&x,&y); if(op==2) update(1,1,n,x,y); if(y<x) swap(x,y); if(op==1) printf("%d\n",query(x,y,1,1,n).ans_sum); } return 0; }
洛谷P4198 楼房重建也是一个线段树维护复杂信息的例子。思考：左右子树的mxn（最大斜率）处理好了以后我们应该如何合并？首先左边的所有本来在这个区间范围内就可以被看到的的楼房肯定都是可以被看到的（即：ans root += ans ls）。那么右边的呢？右边的楼房会有一部分被左边的楼房挡住（其实就是mxn ls），那么挡住以后还会有多少楼房可以被看到呢？显然这不是一个可以O(1) 解决的问题，所以我们考虑直接上暴力搜爆它 将pushup操作log化，即递归实现pushup，对右子树实现一次递归统计。这样时间复杂度就成了 O(n log2 n)，完美解决。在数据范围为1e5~1e6 时，log一下大概会增加20倍复杂度，这是可以接受的（这也是树套树、树剖等算法可以实现的原因）。于是乎我们就可以愉快地递归辽~：
#include <bits/stdc++.h> using namespace std; inline int read() { int num=0; char ch=getchar(); while(!isdigit(ch)) ch=getchar(); while(isdigit(ch)) num=(num<<1)+(num<<3)+(ch^48), ch=getchar(); return num; } const int N=2e5+7; double a[N],mxn[N<<2]; int n,m,len[N<<2]; #define mid ((l+r)>>1) #define ls(p) ((p)<<1) #define rs(p) ((p)<<1|1) inline void pushup1(int p) { mxn[p]=max(mxn[ls(p)],mxn[rs(p)]); } inline int pushup(double lx,int p,int l,int r) { if(mxn[p]<=lx) return 0; if(a[l]>lx) return len[p]; if(l==r) return a[l]>lx; if(mxn[ls(p)]<=lx) return pushup(lx,rs(p),mid+1,r); else return pushup(lx,ls(p),l,mid)+len[p]-len[ls(p)]; } inline void chan(int p,int l,int r,int x,int y) { if(l==r&&l==x) { mxn[p]=(double )y/x; len[p]=1; // printf("%d %d %d %d %.3f %d %d\n",p,l,r,len[p],mxn[p],x,y); return ; } if(x<=mid) chan(ls(p),l,mid,x,y); else chan(rs(p),mid+1,r,x,y); pushup1(p); len[p]=len[ls(p)]+pushup(mxn[ls(p)],rs(p),mid+1,r); // printf("%d %d %d %d %.3f %d %d\n",p,l,r,len[p],mxn[p],x,y); } int main() { scanf("%d%d",&n,&m); int x,y; for(int i=1;i<=m;i++) { scanf("%d%d",&x,&y); a[x]=(double )y/x; chan(1,1,n,x,y); printf("%d\n",len[1]); } return 0; }
洛谷P4247 [清华集训2012]序列操作，这是一道黑题（逃。这个题目要求我们求一个区间所有取m个数的所有方案的和。思考合并方法：若m=10，那么我们可以在左区间选4个数，右区间选6个数，将结果排列组合一遍就会发现ans[10] root += ans[4] ls * ans[6] rs 。即：ans[ i + j ] root += ans[ i ] ls * ans[ j ] rs 。合并解决了我们再来考虑upd。将柿子展开我们会发现一个多项柿，通过这个柿子我们发现ans[ i ] 对ans[ j ]的贡献是（我懒得打了）：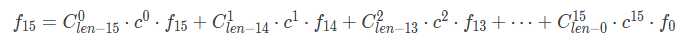 
（引用自dalao Ksum 的博客），预处理出组合数C与c的幂，循环时考虑项 i 对和 j 的贡献，这个柿子就可以O(1) 计算了。上代码：
#include <bits/stdc++.h> using namespace std; typedef long long ll; inline int read() { int num=0,f=1; char ch=getchar(); while(!isdigit(ch)) f=((ch==‘-‘)?-1:1), ch=getchar(); while(isdigit(ch)) num=(num<<3)+(num<<1)+(ch^48), ch=getchar(); return num*f; } const int N=1e5+7,mod=19940417; int n,m; struct s { ll c[21]; int siz,tag_rev; ll tag_add; s() { tag_add=0ll; siz=tag_rev=0; memset(c,0,sizeof(c)); } } t[N<<2]; ll a[N],tgl[N][30],tmp[21]; #define ls (p<<1) #define rs (p<<1|1) #define mid ((l+r)>>1) inline void pushup(int p) { memset(t[p].c,0,sizeof(t[p].c)); for(int i = 0;i <= 20 && i <= t[ls].siz;++i){ for(int j = 0;j + i <= 20 && j <= t[rs].siz;++j){ t[p].c[i + j] += t[ls].c[i] * t[rs].c[j]; } } for(int i = 0;i <= 20 && i <= t[p].siz;++i) t[p].c[i] %= mod; } inline void build(int p,int l,int r) { t[p].siz=r-l+1; t[p].tag_rev=t[p].tag_add=0; if(l==r) { t[p].c[0]=1ll; t[p].c[1]=(a[l] % mod + mod) % mod; return ; } build(ls,l,mid); build(rs,mid+1,r); pushup(p); } inline void add(int p,int l,int r,ll c) { if(!p || !c) return ; memset(tmp,0,sizeof(tmp)); tmp[0]=1ll; for(int i=1;i<=20 && i<=t[p].siz;i++) tmp[i]=tmp[i-1]*c %mod; for(int i=min(t[p].siz,20);i;i--) for(int j=0;j<i;j++) t[p].c[i]=(t[p].c[i] + t[p].c[j] * tmp[i-j] % mod * tgl[t[p].siz-j][i-j]) %mod; t[p].tag_add=(t[p].tag_add + c )% mod; } inline void rev(int p) { if(!p) return ; for(int i=1;i<=20 && i<=t[p].siz;i++) if(i&1) t[p].c[i]=mod - t[p].c[i]; t[p].tag_rev^=1; t[p].tag_add=mod - t[p].tag_add; } inline void pushdown(int p,int l,int r) { if(t[p].tag_rev) { rev(ls); rev(rs); t[p].tag_rev=0; } if(t[p].tag_add) { add(ls,l,mid,t[p].tag_add); add(rs,mid+1,r,t[p].tag_add); t[p].tag_add=0ll; } } inline void update_add(int nl,int nr,int p,int l,int r,ll k) { if(nl<=l && r<=nr) { add(p,l,r,k); return ; } pushdown(p,l,r); if(nl<=mid) update_add(nl,nr,ls,l,mid,k); if(nr>mid) update_add(nl,nr,rs,mid+1,r,k); pushup(p); } inline void update_rev(int nl,int nr,int p,int l,int r) { if(nl<=l && r<=nr) { rev(p); return ; } pushdown(p,l,r); if(nl<=mid) update_rev(nl,nr,ls,l,mid); if(nr>mid) update_rev(nl,nr,rs,mid+1,r); pushup(p); } inline s uni(s x,s y) { s ans; ans.siz=x.siz+y.siz; for(int i=0;i<=x.siz && i<=20;i++) for(int j=0;j<=y.siz && i+j<=20;j++) ans.c[i+j]=(ans.c[i+j] + x.c[i] * y.c[j]) % mod; return ans; } inline s query(int ql,int qr,int p,int l,int r) { if(ql<=l && r<=qr) return t[p]; pushdown(p,l,r); if(qr<=mid) return query(ql,qr,ls,l,mid); else if(ql>mid) return query(ql,qr,rs,mid+1,r); else return uni(query(ql,qr,ls,l,mid),query(ql,qr,rs,mid+1,r)); } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%lld",&a[i]); t[0].c[0]=1ll; tgl[0][0]=1ll; for(int i=1;i<=n;i++) { tgl[i][0]=1ll; for(int j=1;j<=i && j<=20;j++) tgl[i][j]=(tgl[i-1][j]+tgl[i-1][j-1])%mod; } build(1,1,n); char ch[10]; int l,r,x; for(int i=1;i<=m;i++) { scanf("%s",ch+1); scanf("%d%d",&l,&r); if(ch[1]==‘I‘) { scanf("%d",&x); x=(x%mod + mod)%mod; update_add(l,r,1,1,n,x); } if(ch[1]==‘R‘) { update_rev(l,r,1,1,n); } if(ch[1]==‘Q‘) { scanf("%d",&x); printf("%lld\n",(query(l,r,1,1,n).c[x]%mod+mod)%mod); } } return 0; }
≌
代码
标签：数组实现 hellip def 二维线段树 lin 下标 启示 转移 小白
原文地址：https://www.cnblogs.com/2014X/p/13408562.html
