标签:lock 显示 观察 好处 无限 就是 item 正则表达 自动机
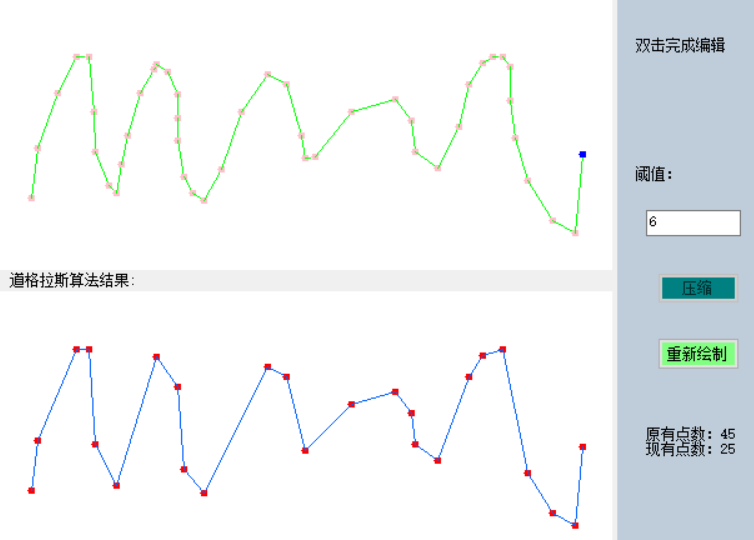
1、道格拉斯-普克算法(Douglas–Peucker)
道格拉斯-普克算法(Douglas–Peucker algorithm,亦称为拉默-道格拉斯-普克算法、迭代适应点算法、分裂与合并算法)是将曲线近似表示为一系列点,并减少点的数量的一种
算法。该算法的原始类型分别由乌尔斯·拉默(Urs Ramer)于1972年以及大卫·道格拉斯(David Douglas)和托马斯·普克(Thomas Peucker)于1973年提出,并在之后的数十年中由其他学者予以完善。
算法的基本思路是:对每一条曲线的首末点虚连一条直线,求所有点与直线的距离,并找出最大距离值dmax ,用dmax与限差D相比:若dmax <D,这条曲线上的中间点全部舍去;若dmax ≥D,保留dmax 对应的坐标点,并以该点为界,把曲线分为两部分,对这两部分重复使用该方法。
简单来讲,其实就是一种压缩算法,对线要素进行压缩,是一个重复的以直代曲的过程。
2、D8单流向算法
ArcGIS水文分析的两个重要的基础,一是使用DEM进行分析,二是分析的基础算法为D8单流向算法。
D8算法是假定雨水降落在地形中某一个格子上,改格子的水流将会流向周围8个格子地形最低的格子中。如果多个像元格子的最大下降方向都相同,则会扩大相邻像元范围,直到找到最陡下降方向为止。如图所示
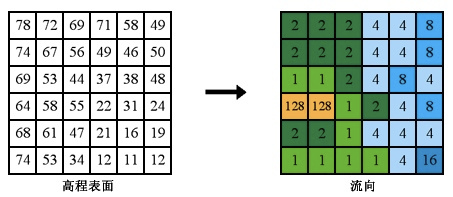
其流向则用2的n次方表示,从0开始,按照逆时针分别为递增,其方位编码如下图所示
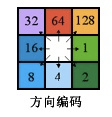
这样编码的好处自然是通过数学的方式,让计算机可以非常快的使用二进制进行索引,加快大区域的流量累计统计。
所以,D8 算法又称作单流向算法。其特点就计算速度快,能够很好的反应出地形对地表径流形成的作用。但其弊端也是显而易见。因为水流只流向一个方向,是单线传递,一旦遇到某一洼地的时候,周边的水流都会集中向该洼地流入,导致断流现象,而现实中由于水会向多个方位不定向的流动,是不会轻易导致断流的。如果要避免这种情况发生,就需要对地形中的洼地进行填平,确保水流也能从该洼地流出。这就是为什么水文分析工具中出现了一些与水文分析完全没有关系的一个工具–填洼 。
从D8算法可以看出,ArcGIS的水文分析工具是依赖无凹陷的DEM地形的,所以在分析之前都必须对DEM数据进行检查。【汇】工具和【填洼】工具就是为了分析前查找和填平洼地而生的,在使用水文分析之前必须要使用这两个工具对DEM进行处理。
单流向算法影响限制了ArcGIS水文分析工具的使用。尤其是地势平坦的地区和人工干预比较多的城市区域,基本上不适用。因为地势平坦导致水流无法沿某一方向流动而形成径流。
另一种情况是事实上的断流形成,如存在地表水流汇流入地下水系的情况。一旦出现流入地下暗河,D8算法就完全失效。因此,在喀斯特地貌中同样也不适用。
D8算法是完全不考虑降雨的多少、土壤渗透率、植被吸水以及水流挡阻等水文过程,它只是假定有无限的降雨并最终汇聚水流形成径流,并通过汇流范围来定义最终的河流。因此,它只是一个径流汇成河流的定性分析(尽管流量计算看起来是有定量因子),并不能通过其流量算法去做水文的预报。


最常用的是D8算法:假设单个栅格中的水流只能流入与之相邻的8 个栅格中。它用最陡坡度法来确定水流的方向,即在3×3 的DEM 栅格上,计算中心栅格与各相邻栅格间的距离权落差(即栅格中心点落差除以栅格中心点之间的距离),取距离权落差最大的栅格为中心栅格的流出栅格。
所谓最陡坡度法的原理是假设地表不透水,降雨均匀.那么流域单元上的水流总是流向最低的地方 “窗口滑动指以计算单元为中心,组合其相邻的若干个单元形成一个窗口”,以“窗口”为计算基本元素,推及整个DEM,求取最终结果。
目前应用最广泛的是基于流向分析和汇流分析的流域特征提取技术。Jenson and Domingue (1988)设计了应用该技术的典型算法,该算法包括3个过程:流向分析,汇流分析和流域特征提取。
流向分析:以数值表示每个单元的流向。数字变化范围是1~255。其中1:东;2:东南;4南;8:西南;16:西;32:西北;64:北;128:东北。除上述数值之外的其它值代表流向不确定,这是由DEM中 洼地”和“平地”现象所造成的。所谓“洼地”即某个单元的高程值小于任何其所有相邻单元的高程。这种现象是由于当河谷的宽度小于单元的宽度时,由于单元的高程值是其所覆盖地区的平均高程,较低的河谷高度拉低了该单元的高程。这种现象往往出现在流域的上游。“平地 指相邻的8个单元具有相同的高程,与测量精度、DEM单元尺寸或该地区地形有关。这两种现象在DEM 中相当普遍,Jenson andDomingue在流向分析之前,将DEM进行填充;将“洼地”变成“平地”,再通过一套复杂的迭代算法确定“平地”流向。
汇流分析:汇流分析的主要目的是确定流路。在流向栅格图的基础上生成汇流栅格图.汇流栅格上每个单元的值代表上游汇流区内流入该单元的栅格点的总数,既汇入该单元的流入路径数(NIP),NIP较大者,可视为河谷,NlP等于0,则是较高的地方,可能为流域s的分水岭。
提取流域特征:有了流域汇流栅格图就可以很方便地提取流域的各种特征参数。例如模拟流域水系,可以设置一个NIP阈值,大于该值的格点为沟谷线上的点,连接各个沟谷线上的点就形成了河网。在汇流矩阵(汇流栅格)上求子流域的方法如下:从河谷单元或孤立的洼单元开始,向上游搜索所有流向该单元的单元,这些单元构成以开始单元为流域出口的子流域。模拟出水系及流域边界后,利用GIS的相关函数,就可以很方便地得到流域的各项特征参数,如河流的长度、坡癣、流域面积等。
详细介绍
3、不规则多边形面积计算
这个算法的思想就是不停地将多边形,划分成n个三角形,然后计算每个三角形的面积,这个可以用线性代数的知识解决。
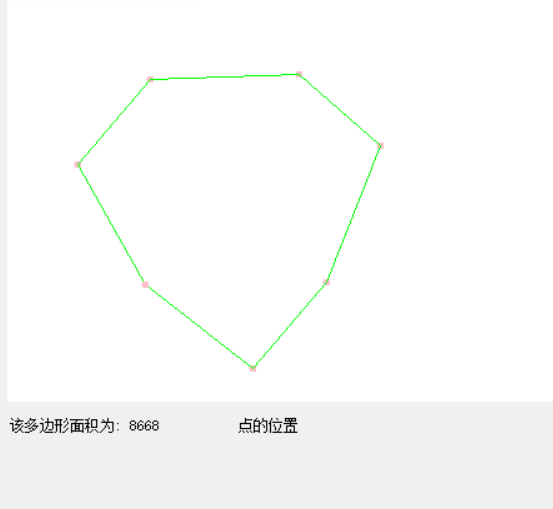
大家可以参考这个网址https://blog.csdn.net/lemongirl131/article/details/51130659
无论是凸多边形还是凹多边形都是适用的。
4、点在多边形内外的判断
① 角度和法
首先,假如在一个二维平面上,有一个多边形和一点P,按顺时针或逆时针方向计算每两点与点P的角度求和,若角度和<360°(2π),则点P在多边形外;若角度和=360°(2π),则点P在多边形内;若角度和=180°(π),则点P在多边形上;
② 射点法
首先,假如在一个二维平面上,有一个多边形和一点P,从该点处向某一方向做一条射线,若点P在多边形外,则该射线与多边形的交点个数必为偶数(包括0);若点P在多边形内,则该射线与多边形的交点个数必为奇数。
还有一些特殊情况要考虑。假如考虑边(P1,P2),
1)如果射线正好穿过P1或者P2,那么这个交点会被算作2次,处理办法是如果P的从坐标与P1,P2中较小的纵坐标相同,则直接忽略这种情况
2)如果射线水平,则射线要么与其无交点,要么有无数个,这种情况也直接忽略。
3)如果射线竖直,而P0的横坐标小于P1,P2的横坐标,则必然相交。
4)再判断相交之前,先判断P是否在边(P1,P2)的上面,如果在,则直接得出结论:P再多边形内部。
③ 叉乘法
想象一个凸多边形,将凸多边形中每一个边AB,与被测点P,求PA×PB。判断结果的符号是否发生变化,如果没有变化,P在多边形内;反之点处于凸多边形外。但对于凹多边形不再适用。 其每一个边都将整个2D屏幕划分成为左右两边,连接每一边的第一个端点和要测试的点得到一个矢量v,将两个2维矢量扩展成3维的,然后将该边与v叉乘,判断结果3维矢量中Z分量的符号是否发生变化,进而推导出点是否处于凸多边形内外。这里要注意的是,多边形顶点究竟是左手序还是右手序,这对具体判断方式有影响。
前两种方法适合于所有多边形,最后一种只适合凸多边形。
5、曼哈顿距离算法(Manhattan Distance)
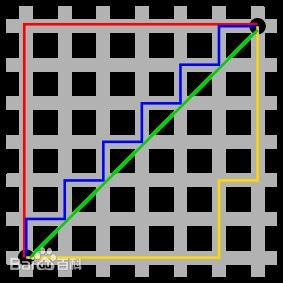
图中红线代表曼哈顿距离,绿色代表
欧氏距离,也就是
直线距离,而蓝色和黄色代表等价的曼哈顿距离。
曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离,即d(i,j)=|xi-xj|+|yi-yj|。对于一个具有正南正北、正东正西方向规则布局的城镇街道,从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离,因此,曼哈顿距离又称为出租车距离。曼哈顿距离不是距离不变量,当坐标轴变动时,点间的距离就会不同。曼哈顿距离示意图在早期的计算机图形学中,屏幕是由像素构成,是整数,点的坐标也一般是整数,原因是浮点运算很昂贵,很慢而且有误差,如果直接使用AB的欧氏距离(欧几里德距离:在二维和三维空间中的欧氏距离的就是两点之间的距离),则必须要进行浮点运算,如果使用AC和CB,则只要计算加减法即可,这就大大提高了运算速度,而且不管累计运算多少次,都不会有误差。
曼哈顿距离算法,简单来讲其实就是根据曼哈顿距离来计算最优路径的算法,是一种启发式的寻路算法,对网络结构的要求是规则。
6、迪杰斯特拉算法(Dijkstra)
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。
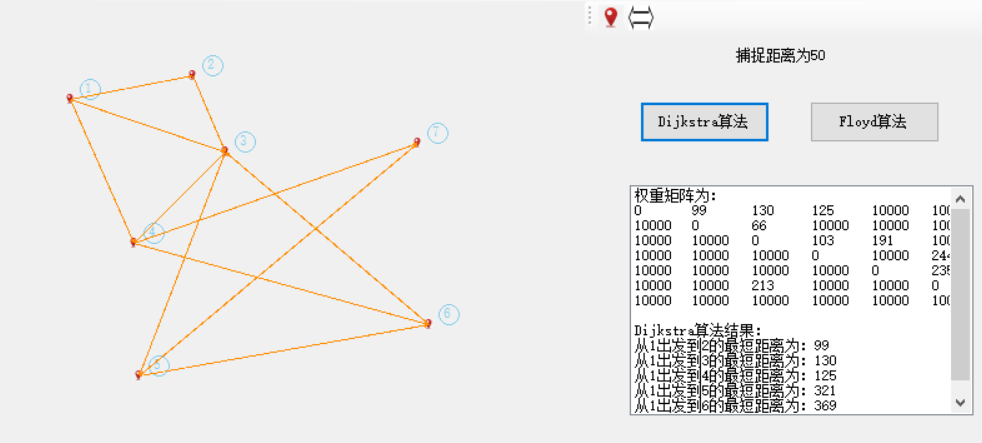
Dijkstra算法,简单讲是一种贪心算法,通关权重矩阵进行计算,利用广度优先算法不停找其相邻点的过程,这个可以参考百度,百度说的很清楚。
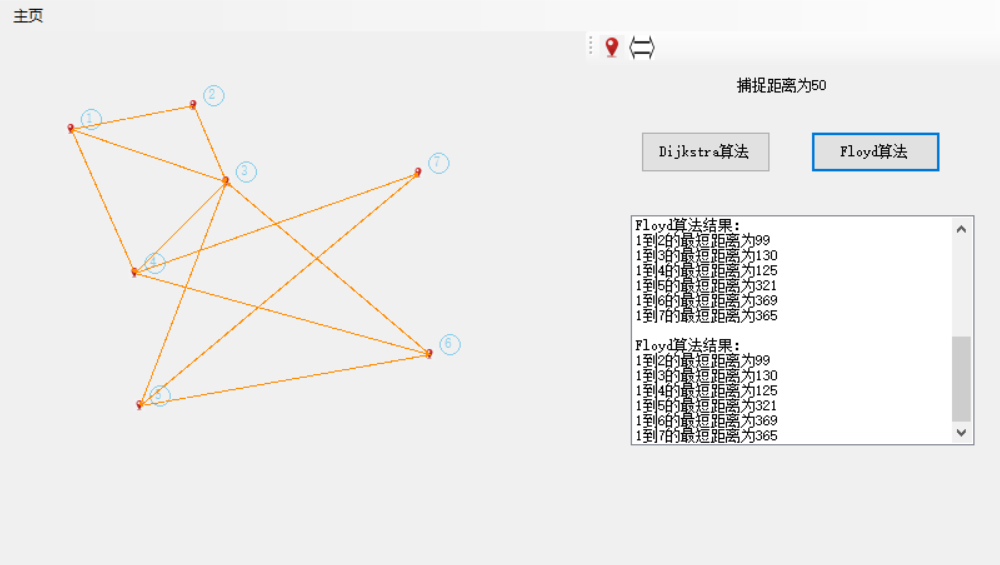
7、弗洛伊德算法(Floyd)
在计算机科学中,Floyd-Warshall算法是一种在具有正或负边缘权重(但没有负周期)的加权图中找到最短路径的算法。算法的单个执行将找到所有顶点对之间的最短路径的长度(加权)。 虽然它不返回路径本身的细节,但是可以通过对算法的简单修改来重建路径。 该算法的版本也可用于查找关系R的传递闭包,或(与Schulze投票系统相关)在加权图中所有顶点对之间的最宽路径。
Floyd-Warshall算法是
动态规划的一个例子,并在1962年由Robert Floyd以其当前公认的形式出版。然而,它基本上与Bernard Roy在1959年先前发表的算法和1962年的Stephen Warshall中找到图形的传递闭包基本相同,并且与Kleene的算法密切相关 在1956年)用于将确定性有限自动机转换为正则表达式。算法作为三个嵌套for循环的现代公式首先由Peter Ingerman在1962年描述。
该算法也称为Floyd算法,Roy-Warshall算法,Roy-Floyd算法或WFI算法。
Floyd算法,简单讲就是三层循环遍历,这个也可以参考百度。Dijkstra算法和Floyd算法跟计算机专业联系密切,不仅用于GIS中图的最短路径的研究,在运筹学等多方面应用广泛,博主在前段时间的一个电影较大数据的人物关系查询还曾用到这两个算法,希望读者可以深入了解下。
8、泰森多边形(Voronoi图)
泰森多边形又叫冯洛诺伊图(Voronoi diagram),得名于Georgy Voronoi,是一组由连接两邻点线段的垂直平分线组成的连续多边形组成。一个泰森多边形内的任一点到构成该多边形的控制点的距离小于到其他多边形控制点的距离。泰森多边形是对空间平面的一种剖分,其特点是多边形内的任何位置离该多边形的样点(如居民点)的距离最近,离相邻多边形内样点的距离远,且每个多边形内含且仅包含一个样点。由于泰森多边形在空间剖分上的等分性特征,因此可用于解决最近点、最小封闭圆等问题,以及许多空间分析问题,如邻接、接近度和可达性分析等。
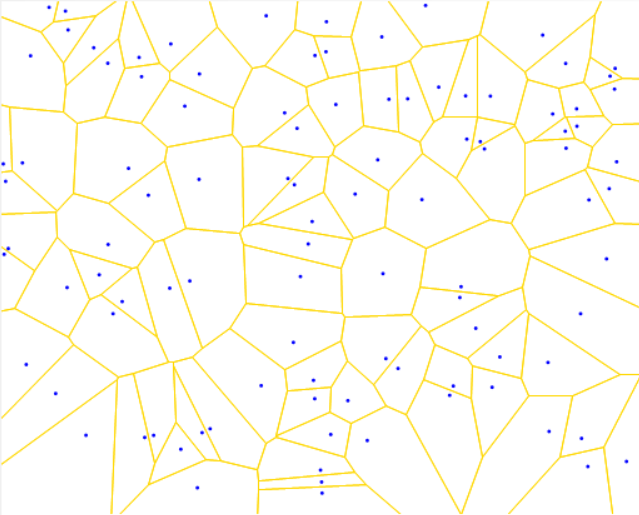
也就是我们常说的Voronoi图,百度讲的也比较清楚。
9、狄洛尼三角网(Delaunay )
这个需要先讲一下TIN,我们常说的TIN就是不规则三角网。
不规则三角网(TIN, Triangulated Irregular Network)模型采用一系列相连接的三角形拟合地表或其他不规则表面,常用来构造数字地面模型,特别是数字高程模型。最常用的生成方法是Delaunay 剖分方法。TIN在表示复杂表面方面具有许多优越性,国面被广就应用于数字制用、地用表面的模型化及分析以及LIS中。
在所有可能的三角网中,狄洛尼(Delaunay)三角网在地形拟合方面运用的较普遍,因此常被用于TIN的生成。在狄洛尼三角网中的每个三角形可视为一个平面,平面的几何特征完全由三个顶点的空间坐标值(x,y,z)所决定。存储的时候,每个三角形分别构成一个记录,每个记录包括:三角形标识码、该三角形的相邻三角形标识码、该三角形的顶点标识码等。顶点的空间坐标值则另外存储。
狄洛尼三角网是在所有可能的三角网中,Delaunay 三角网在离散点均匀分布的情况下能够避免产生有过小锐角的三角形。
在地形拟合方面也表现得最为出色,所以,人们一般把TIN构建成Delaunay 三角网。

Delaunay三角网,全称应该是狄洛尼不规则三角网(Delaunay Triangulated Irregular Network),主要就是应用于TIN的构建,立体模型的生成。
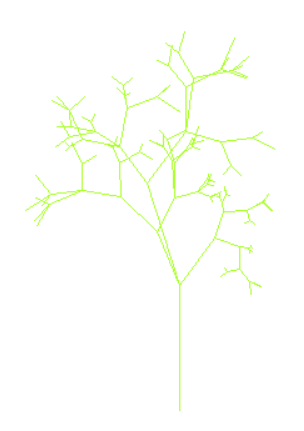
10、分形图
人们谈论分形,常常有两种含义。
其一,它的实际背景是什么?其二,它的确切定义是什么?
数学家研究分形,是力图以数学方法,模拟自然界存在的、及科学研究中出现的那些看似无规律的各种现象。在过去的几十年里,分形在物理学、
材料科学、地质勘探、乃至股价的预测等方面都得到了广泛的应用或密切的注意,并且由于分形的引入,使得一些学科焕发了新的活力。数学上所说的分形,是抽象的。而人们认为是分形的那些自然界的具体对象,并不是数学家所说的分形,而是不同层次近似。
1985年,曼德布罗特获得Barnard奖章。这项奖励专门颁发给那些在物理科学或者其它自然科学中有重大贡献、有重大影响的人物。在每五年一次的获奖者名单中,有爱因斯坦、费米这样一批享誉世界的科学家,可见曼德布罗特的分形研究在科学上的地位和影响。1995年应中国科学界的邀请,曼德布罗特访问中国并进行演讲。
分形图形同常见的工程图迥然不同,分形图形一般都有自相似性,这就是说如果将分形图形的局部不断放大并进行观察,将发现精细的结构,如果再放大,就会再度出现更精细的结构,可谓层出不穷,永无止境。艺术家在分形画面的不同区域涂上不同的色彩,展现在我们面前的,将会是非常美丽的画面。
几乎在曼德布罗特获得Barnard奖章的同时,以德国布来梅大学的数学家和计算机专家H.Peotgen与P.Richter等为代表,在当时最先进的计算机图形工作站上制作了大量的分形图案;J. Hubbard等人还完成了一部名为《混沌》的计算机动画。接着,印刷着分形的画册、挂历、明信片、甚至T恤衫纷纷出笼。
80年代中期开始,首先在西方发达国家,接着在中国,分形逐渐成为脍炙人口的词汇,甚至连十几岁的儿童也迷上了计算机上的分形游戏。
我国北京的北方工业大学计算机图形学小组于1992年完成了一部计算机动画电影《相似》,这部电影集中介绍了
分形图形的相似性,这也是我国采用计算机数字技术完成的第一部电影,获得当年电影电视部颁发的科技进步奖。
更多的人陶醉于分形,并非出自科学,而是倾心于分形之美。数学上的审美很难为一般人所理解:一大堆数字、公式、符号怎么体现出来呢?然而,计算机能让数学的某些内在的美直
观呈现出来,给出其形式化的表达。分形作为一类例证,为数学理论与实践中所蕴涵的美,给出了一类精彩的注记。充分反映了数学科学中的简单、和谐、统一的内涵!
一方面,从来不以科学内容本身为主题的艺术创作,也大量引用“动力系统”、“迭代逼近”、“混沌吸引子”等科学术语,进而极力采用计算机绘图手段,创造出无比神奇的作品。由这一点出发,可以说,艺术家已经开始漫步于科学领地!
另一方面,一向以严肃表情面向读者的科学著作一反常态,书名也竟然浪漫起来:《The Beauty of Fractals》(分形之美)(1986),《Fractals Everywhere》(分形处处可见),《The Algorithmic Beauty of Plants》(植物算法中的美)(1990), ….大量精美的、显示分形的科学挂图,乔装打扮,在美术馆展厅登场,接受艺术鉴赏家的评头论足,科学家也从此跨入了神圣的艺术殿堂!
分形图(11张)
分形之美,往往须经计算机的处理才能表现出来的。今天,人们可以在网络上,浏览与欣赏各种不同风格的分形作品,有的针对科学研究中要表达的一些特别的对象,有的则完全是艺术。网络天地会给你提供许多、美妙惊奇的分形图画,令你心犷神怡,也有时令你眼花缭乱。
关于分形图,大家也可以看百度,简单的了解没有问题,当然博主更推荐相关书籍。
至于算法的重要性,算法是计算机科学领域最重要的基石之一,对于编程者来说,算法是解决问题的一种重要手段,现在不少人陷入了一个误区,认为只有前沿的知识才是最重要的,这使他们在追逐前沿技术时忘记了那些根本的基础的工具,整天赶时髦的人最后只懂得招式,没有功力,是不可能成为高手的。
文中只提到了一些常用的GIS相关的算法,博主会在之后对这些相关算法的源码进行公布,欢迎评论或后台留言!

扫码关注公众号
盘点十大GIS相关算法
标签:lock 显示 观察 好处 无限 就是 item 正则表达 自动机
原文地址:https://www.cnblogs.com/pygisxss/p/13440426.html