C++面对对象（一）

标签：机器   增加   lan   static   完成   隐式   运算   不用   方法   

课程地址：数据结构与算法 | 第四周辅导 红皮第七章 面向对象方法（一）

1. 程序设计方法：

   • 结构化程序设计
   • 面向对象的程序设计
     • 类
     • 对象

2. 类

   • 变量：描述对象属性（数据成员）
   • 函数：描述对象行为（成员还是）

3. 定义类

   有三种访问控制方式：

   class 类名 {
       public:    公有成员：任何地方都可以访问
       private:   私有成员：该类 成员函数
       protected: 保护成员：该类 + 派生类 成员函数
                  友元函数(特殊)：随便访问
   }
   

   注意：

   • 不写访问控制方式，默认private
   • 类的友元可以访问类及其派生类的任何东西

4. 构造函数

   形式区别：

   // 构造函数
   <类名> (形参表){
       函数体
   }
   
   // 一般函数
   <返回类型> <函数名>（形参表{
       函数体
   }
   

   参数：

   • 有参
   • 无参

   返回值：

   • 无值 void （可以没有return，或者return;）
   • 有值

   构造函数特殊：

   • 构造函数没有任何返回类型，不可以写 void

   • 函数名就是类名（判断一个函数是否为构造函数的依据）

   • 可以重载（有参/无参）

     函数重载：C++中不同的函数有相同的函数名。以传入实参的数量/类型来决定调用哪个函数。

   • 类定义中，若未写构造函数，系统提供一个无函数体的无参构造函数

   • 作用：

     1. 为对象分配内存空间
     2. 完成对该对象数据成员的初始化操作

   • 如果在创建新对象的时候，构造函数由系统自动调用。

     若一个对象已经被创建，再进行显示调用的时候，就会报错。

     // 初始化自动调用有参的
     Circle circleC(3.5, 4.5, 45.6);
     // 再次显示调用，报错
     corcleC.circle(3.5, 4.5, 45.6);
     

     调用类对象方法：

     对象.方法
     指针->方法
     

5. 析构函数

   // 析构函数不可以有形参
   virtual ~<类名> (){
       函数体，销毁对象
   }
   

   特点：

   1. 没有任何返回类型
   2. 函数名就是类名
   3. 只可以无参（一定不可重载）
   4. 类定义中未定义析构函数，系统提供一个没有函数体的析构函数。
   5. 最好+\(virtual\)

   作用：

   • 在对象生存周期结束后，“善后工作”（比如我们new出来的内存，要进行删除）

6. 拷贝构造函数

   作用：用一个已存在对象来初始化一个正在创建的新对象

   特点：

   1. 函数名也是类名

   2. 形参只有一个，是对象的引用

   3. 也是构造函数，所以没有返回类型

   4. 函数原型

       <类名>(<类名> &对象名)
      

      函数原型：形参表中给出形参个数、类型，不用给具体名称。

      

      为什么参数是这样的：类 对象 关系 ==> 数据类型 变量 关系：Circle (Circle &circle)

      ---

      拷贝类型：

      • 浅拷贝（默认、系统自带）
      • 深拷贝（用户自定义）

      // 调用有参构造
      IntArray x(20);
      // 调用拷贝构造(用x去初始化y)
      IntArray y(x); 
      

      浅拷贝：指向同一块内存区域，析构2次

      

7. 类声明和实现分离（函数定义与函数声明）

   • 类声明（放在头文件 .h 中）

     用途：描述类的结构

     • 类的数据成员
     • 有哪些成员函数
     • 友元函数

   • 类实现（放在源文件 .cpp 中）

     用途：描述成员函数具体的功能

   注意：

   • .cpp中写出 #include “*.h”

     • ”" 先在当前文件夹搜索，再到系统默认文件夹搜索
     • <> 直接在系统默认文件夹搜索

   • 类实现中成员函数形式：

     // 普通函数
     <返回类型> <函数名>(形参表){
         函数体
     }
     // 成员函数 
     <返回类型> <类名>::<函数名>(形参表){
         函数体
     }
     

     • 增加<类名>::，指出所定义的成员函数属于哪个类 （::作用域运算符）

   为啥要分离？

   1. 保密
   2. 加快编译（链接）

8. 类的静态数据成员

   特点：

   • 类内声明(.h)、类外初始化（.cpp）
   • 该变量所有由该类派生的对象共享（修改同步）

   // .h
   static int x;
   

   // .cpp
   // 静态
   <类型> <类名>:: <变量> = <初值> ;
   

   只要是类声明和实现的分离，就一定要写清楚，这个变量、函数属于谁。

   • 静态成员变量要在类定义中声明，在类外进行初始化（前者说明，它还是属于这个类的，后者是因为这个变量要存在全局变量区，C++还是面向机器的语言）
   • 类外初始化不用static

9. 类的常量成员

   • 数据成员，语法： const int x;

     注意：

     • 常量数据成员在声明时候不可被赋初值，在定义对象时，利用构造函数赋初值，有值后就不可修改。
     • 普通数据成员，也最好在构造函数里。

   • 成员函数，语法：<类型> <函数名> (形参表) const，只可读，不可写

10. this 指针（非静态成员函数）

    • 隐式调用：，默认会隐式调用this指针

    • 显示调用：

      • 形参名，与类的数据成员名相同

        Point (float x, float y){
            this->x = x; // x = x??? 
            this->y = y; // 等价于 Point.x = x;
        }
        

      • 返回值，对象本身，或者这个对象的地址（this ~ &对象名）

        • 对象地址：return this
        • 对象本身（取地址值）：return *this

11. 友元

    为什么要出现友元？

    一个类中的函数，一般无法直接访问另一个类中私有/保护成员，我们用友元函数来做。好处：提高了程序的效率，坏处：破坏了封装性

    友元：

    • 友元函数：将某个函数声明为友元函数，该函数，可以访问同一个类中任何成员

      定义：

      friend <函数类型> <函数名>(<形参表>);
      

    • 友元成员：将一个类中成员函数A，声明为另一个类B的友元函数

      用途：在A类中的一个函数，可以访问B中任一成员变量（B说，A是我的朋友，A可以访问B类的任何东西）

      定义（两步法）：

      • 在 A 类中声明成员函数

        class A {
            int func (int x);
        }
        

      • 在 B 类中声明 A 类的成员函数，作为B类的友元（B的资源可以任意访问）

        class B {
            // A::** 将 A 类中的func放进来
            friend int A:: func(int x);
        }
        

    • 友类：A类中所有成员函数，均可访问B类中所有成员。

      定义（两步法）：

      • 先定义A 类

        class A {
            
        }
        

      • 在B类中声明A是B的友类：

        class B{
            // 把A类作为B的朋友（朋友）
            freind class A;
        }
        

      注意：

      • 单向性：A是B的友类，B不是A的友类。
      • 非传递性：A是B的友类，B是C的友类，A不是C的友类

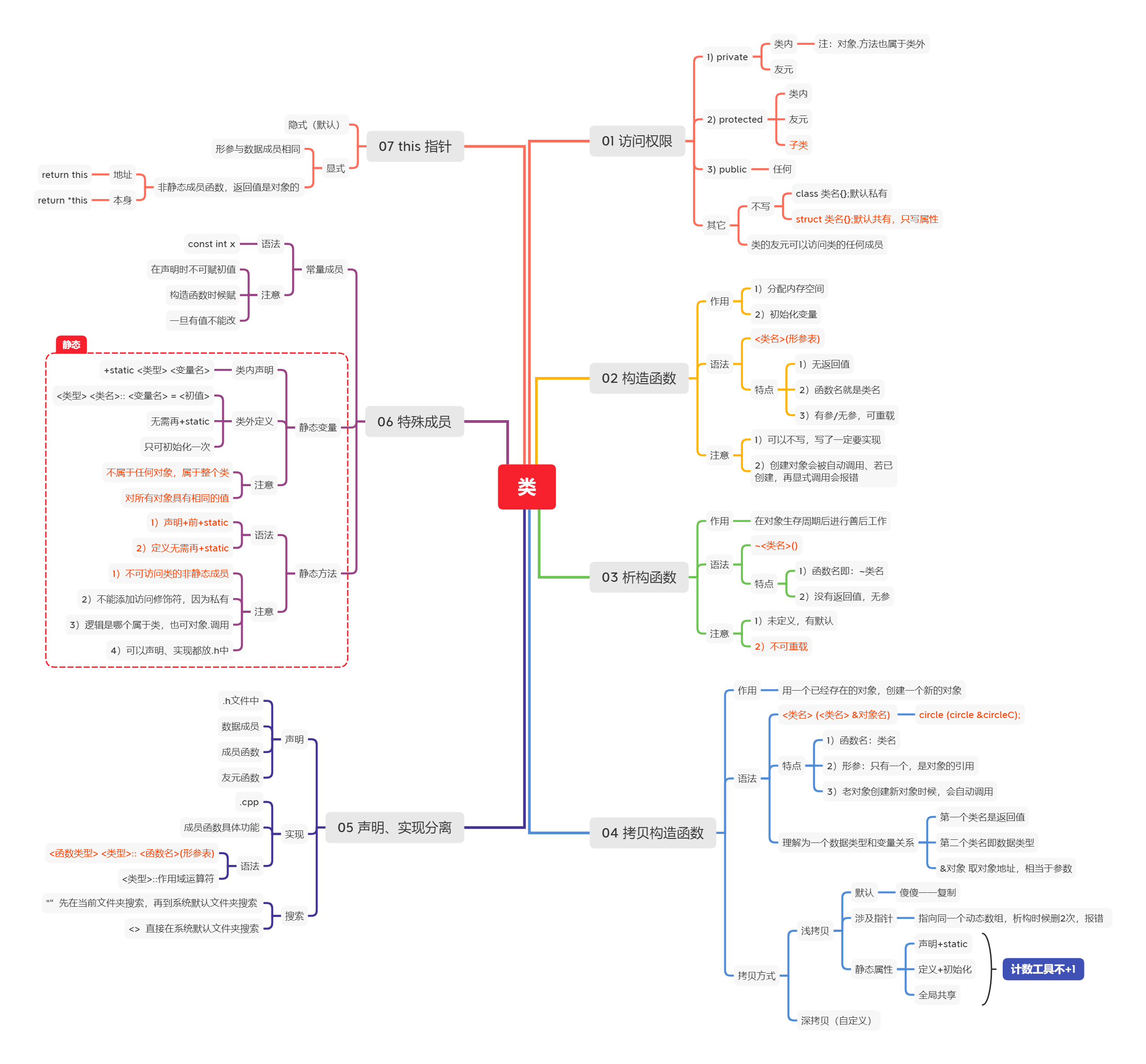
思维导图：

C++面对对象（一）

标签：机器   增加   lan   static   完成   隐式   运算   不用   方法   

原文地址：https://www.cnblogs.com/FLYMANJB/p/13574233.html