标签:width size 表示 大小 顺序 自己的 注意 端点 匈牙利算法
本文讲述的是匈牙利算法,即图论中寻找最大匹配的算法,暂不考虑加权的最大匹配(用KM算法实现),文章整体结构如下:
好的,开始!
一. 部分基础概念的介绍
我会严格介绍其定义,并同时用自己的大白话来重述。
概念点1. 图G的一个匹配是由一组没有公共端点的不是圈的边构成的集合。
这里,我们用一个图来表示下匹配的概念:
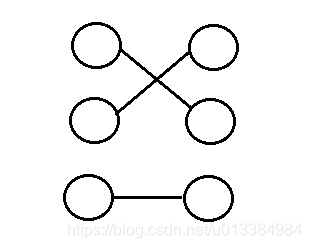
如图所示,其中的三条边即该图的一个匹配;所以,匹配的两个重点:1. 匹配是边的集合;2. 在该集合中,任意两条边不能有共同的顶点。
那么,我们自然而然就会有一个想法,一个图会有多少匹配?有没有最大的匹配(即边最多的匹配呢)?
我们顺着这个思路,继续往下走。
概念点2. 完美匹配:考虑部集为X={x1 ,x2, ...}和Y={y1, y2, ...}的二部图,一个完美匹配就是定义从X-Y的一个双射,依次为x1, x2, ... xn找到配对的顶点,最后能够得到 n!个完美匹配。
这里有一个概念,有点陌生,即什么是二部图,这个其实很好理解,给定两组顶点,但是组内的任意两个顶点间没有边相连,只有两个集合之间存在边,即组1内的点可以和组2内的点相连,这样构建出来的图就叫做二部图(更好理解就是n个男人,n个女人,在不考虑同性恋的情况下,组成配偶)。这样是不是简单多了?
既然说到了双双组成配偶,那我们干的就是月老做的活了,古话说得好,宁拆一座庙,不毁一桩婚,如果真的给出n个帅气的男孩,n个漂亮的女孩,他们之间互相有好感,但一个男孩可以对多个女孩有感觉,一个女孩也可能觉得多个男孩看起来都不错,在这种情况下,我们怎么让他们都能成双成对呢?
将这个问题抽象出来,互有好感就是一条条无向边(单相思我们先不考虑),而男孩和女孩就是一个个节点,我们构建出这么一个图,而完美匹配就是让所有看对眼的男孩和女孩都能够在一起。
完美匹配是最好的情况,也是我们想要的情况。
当然,有些情况下我们做不到完美匹配,只能尽可能实现最多的配对,这个就叫做最大匹配。
可以看出来,完美匹配一定是最大匹配,而最大匹配不一定是完美匹配。
那么,作为月老的我们,核心目标就是找到最大匹配了。
在我们思考如何完成这个艰巨的任务之前,我们引入几个可能不太好理解的概念。
3.交错路径:给定图G的一个匹配M,如果一条路径的边交替出现在M中和不出现在M中,我们称之为一条M-交错路径。
而如果一条M-交错路径,它的两个端点都不与M中的边关联,我们称这条路径叫做M-增广路径。
举个例子:
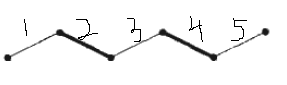
在上图中,有五条边,按照匹配的概念,2, 4两条加粗的边是一个匹配,目光锐利的你或许同时发现了,1, 3, 5是不是也是一个匹配呢?
毫无疑问,是的。
套用我们说的M-交错路径的概念,如果我们从2, 4 所构成的匹配M出发,会发现 1, 2, 3, 4, 5 这条路径是M的一条交错路径,同时它还满足两个端点都不与M中的边所关联。
是不是发现个奇怪的地方呢?我们完全可以从1, 2, 3, 4, 5 这条路径中找到一个更大的匹配,而这个匹配比原先的匹配M多一条边,是一个比原先M更大的匹配!
所以,我们寻找最大匹配的任务就相当于我们不断地在已经确定的匹配下,不断找到新的增广路径,因为出现一条增广路径,就意味着目前的匹配中增加一条边嘛!
看起来复杂的问题,变成了寻找增广路径这么个解决问题的想法了。
当图中再没有增广路径了,就意味着我们找到了该图的最大匹配了。
说明下:我们这里所讨论的匹配,是图论中的任务分配问题,通常是针对于二部图发起的,想想也是,匹配不就是配对么,自然是两两成对了。
好,基础概念介绍完了,我们接下来给个例子,探讨我们的匈牙利算法,它就是通过不断寻找增广路径的办法,打开了通向最大匹配的道路。
二. 匈牙利算法
下面我们讨论下匈牙利算法的内容:
1. 给定一个图:
前面已经说了,我们讨论的基础是二部图,而上图就是一个二部图,我们从上图的左边开始讨论,我们的目标是尽可能给x中最多的点找到配对。
注意,最大匹配是互相的,如果我们给X找到了最多的Y中的对应点,同样,Y中也不可能有更多的点得到匹配了。
刚开始,一个匹配都没有,我们随意选取一条边,(x1, y1)这条边,构建最初的匹配出来,结果如下,已经配对的边用粗线标出:
2. 我们给x2添加一个匹配,如下图的(x2, y2)边。
目前来看,一切都很顺利,到这里,我们形成了匹配M,其有(x1, y1), (x2, y2 ) 两条边。
3. 我们现在想给x3匹配一条边,发现它的另一端y1已经被x1占用了,那x3就不高兴了,它就去找y1游说,让y1离开x1。
即将被迫分手的x1很委屈,好在它还有其他的选择,于是 x1 妥协了,准备去找自己看中的y2。
但很快,x1发现 y2 被x2 看中了,它就想啊,y1 抛弃了我,那我就让 y2 主动离开 x2 (很明显,这是个递归的过程)。
x2 该怎么办呢?好在天无绝人之路,它去找了y5。
谢天谢地,y5 还没有名花有主,终于皆大欢喜。
匹配如下:
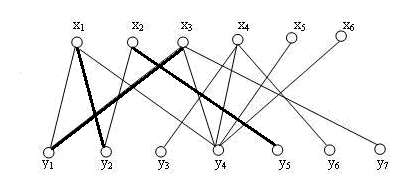
上面这个争论与妥协的过程中,我们把牵涉到的节点都拿出来:(x3, y1, x1, y2, x2, y5),很明显,这是一条路径P。
而在第二步中,我们已经形成了匹配M,而P呢?还记得增广路径么,我们发现,P原来是M的一条增广路径!
上文已经说过,发现一条增广路径,就意味着一个更大匹配的出现,于是,我们将M中的配对点拆分开,重新组合,得到了一个更大匹配,M1, 其拥有(x3, y1),(x1, y2), (x2, y5)三条边。
而这,就是匈牙利算法的精髓。
同样,x4 , x5 按顺序加入进来,最终会得到本图的最大匹配。
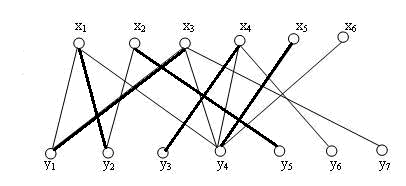
得到这个结果后,我们发现,其实也可以把y4 让给 x6 , 这样x5 就会空置,但并不影响最大匹配的大小。
总结:
1. 匈牙利算法寻找最大匹配,就是通过不断寻找原有匹配M的增广路径,因为找到一条M匹配的增广路径,就意味着一个更大的匹配M‘ , 其恰好比M 多一条边。
2. 对于图来说,最大匹配不是唯一的,但是最大匹配的大小是唯一的。
标签:width size 表示 大小 顺序 自己的 注意 端点 匈牙利算法
原文地址:https://www.cnblogs.com/sqm724/p/13614193.html