标签:alt 怎么 prime 图像 记忆 book mil nlog lock
所有代码若无说明,均采用快读模板
关于质数,无非就两大类:
先讲1:
判断x是不是质数
根据质数的定义,我们可以枚举所有小于x,大于1的正整数i。如果x%i==0,即i是x的因数,则x不是质数。
很明显,一个质数的因数是成对出现,且分别在sqrt(x)的两边。所以只要枚举到sqrt(x)即可。
bool judge(LL & x) { if(x<2) return 0; LL sq=sqrt(x); for(re LL i=2;i<=sq;i++) { if(!(x%i)) return 0; } return 1; }
时间复杂度O(sqrt(n))
那么,这里插一句嘴——只要再从1~n枚举一个数,不就可以得出1~n中所有的质数了嘛?!
(另外一种判断质数的方法等会再讲)
上面是指极限下1s能过的数据
bool judge(LL & x)//n=1.5*10^6 这里用IL反而会慢0.01s { if(x<2) return 0; LL sq=sqrt(x); for(re LL i=2;i<=sq;i++) { if(!(x%i)) return 0; } return 1; } LL n; int main() { freopen("prime.in","r",stdin); freopen("nsqrtn.out","w",stdout); n=read(); for(re LL i=1;i<=n;i++) { if(judge(i)) write(i); } return 0; }
时间复杂度O(nsqrt(n))
这里只要把上面的那个n=1.5*10^6做一个小小的优化(可以理解为记忆化)
其实,我们在尝试枚举因数的时候,我们可以只要枚举质因数就好。
比如x=91
如果我枚举到i=2(某个质数)发现不能整除,那么91当然也不能被2的倍数(质数的(2倍以上的)倍数是不是质数)整除啊
所以,judge()中的枚举i只需要枚举1~sqrt(x)中的质数即可。
使用一个数组存储所有的质数吧。
LL his[1000000]; LL size; bool judge(LL & x)//n=4*10^6 { if(x<2) return 0; LL sq=sqrt(x); for(re LL i=0;his[i]<=sq&&i<size;i++) { if(!(x%his[i])) return 0; } return 1; } LL n; int main() { freopen("prime.in","r",stdin); freopen("nsqrtnpro.out","w",stdout); n=read(); his[size++]=2; if(n>=2) write(2); for(re LL i=3;i<=n;i++) { if(judge(i)) write(i),his[size++]=i; } return 0; }
时间复杂度O(?)
接下来在看看
这次是埃氏筛(埃拉托斯特尼筛法)。
每找到一个质数,就将它的倍数打上标记即可。
如果循环到某个数的时候,它没有被打上标记
那么它就一定是质数了,
就再拿它去更新它的倍数。
bool book[30000000]; LL prime[30000000]; LL size; LL n; int main()//n=3*10^7 { freopen("prime.in","r",stdin); freopen("Eratosthenes.out","w",stdout); n=read(); book[1]=1; prime[size++]=2; for(re LL i=2;i<=n;i++) { if(!book[i]) { prime[size++]=i; write(i); for(re LL j=2;i*j<=n;j++) { book[i*j]=1; } } } return 0; }
时间复杂度O(nloglogn),已经非常接近于线性的了
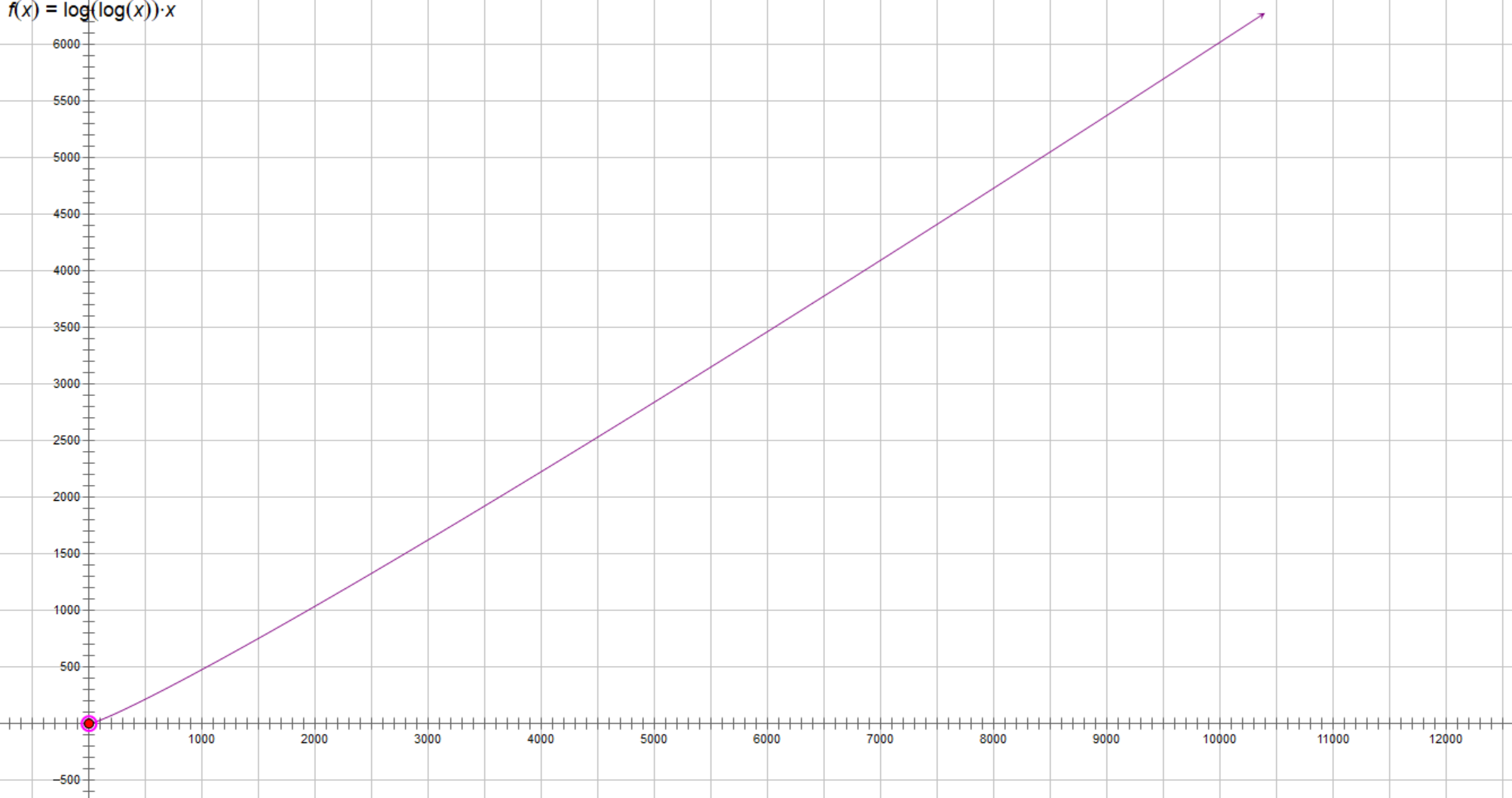
(注意,虽然它的图像在10000以内的斜率看似比y=x还要小,但是我们比较的是其增长性,即:nloglogn的导数是单调递增的)
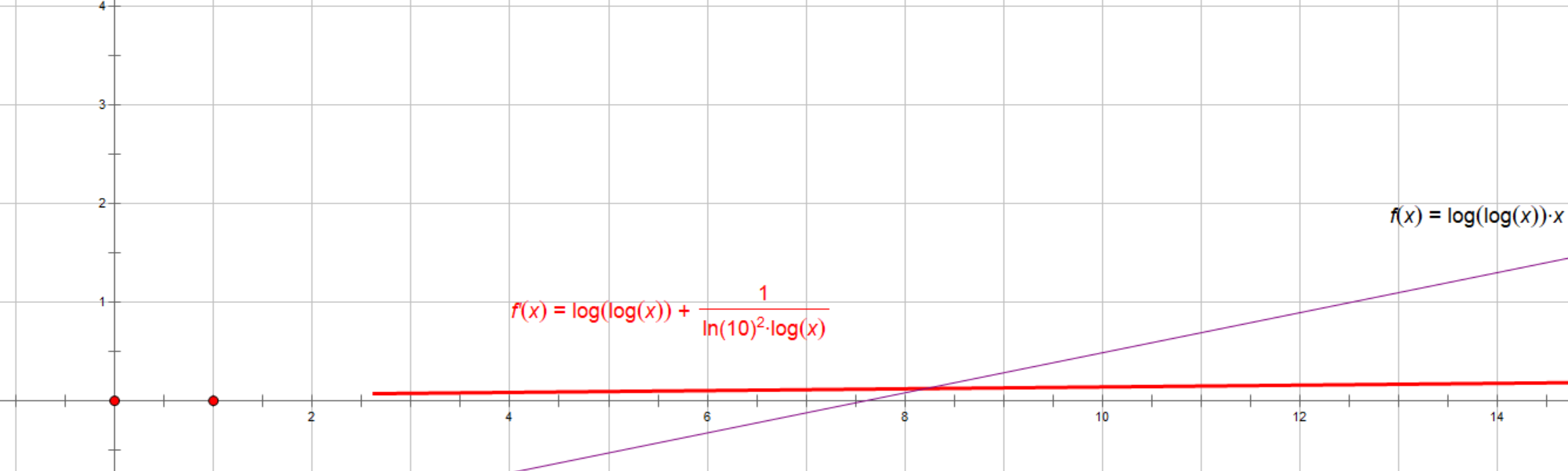
可能一阶导看不出来
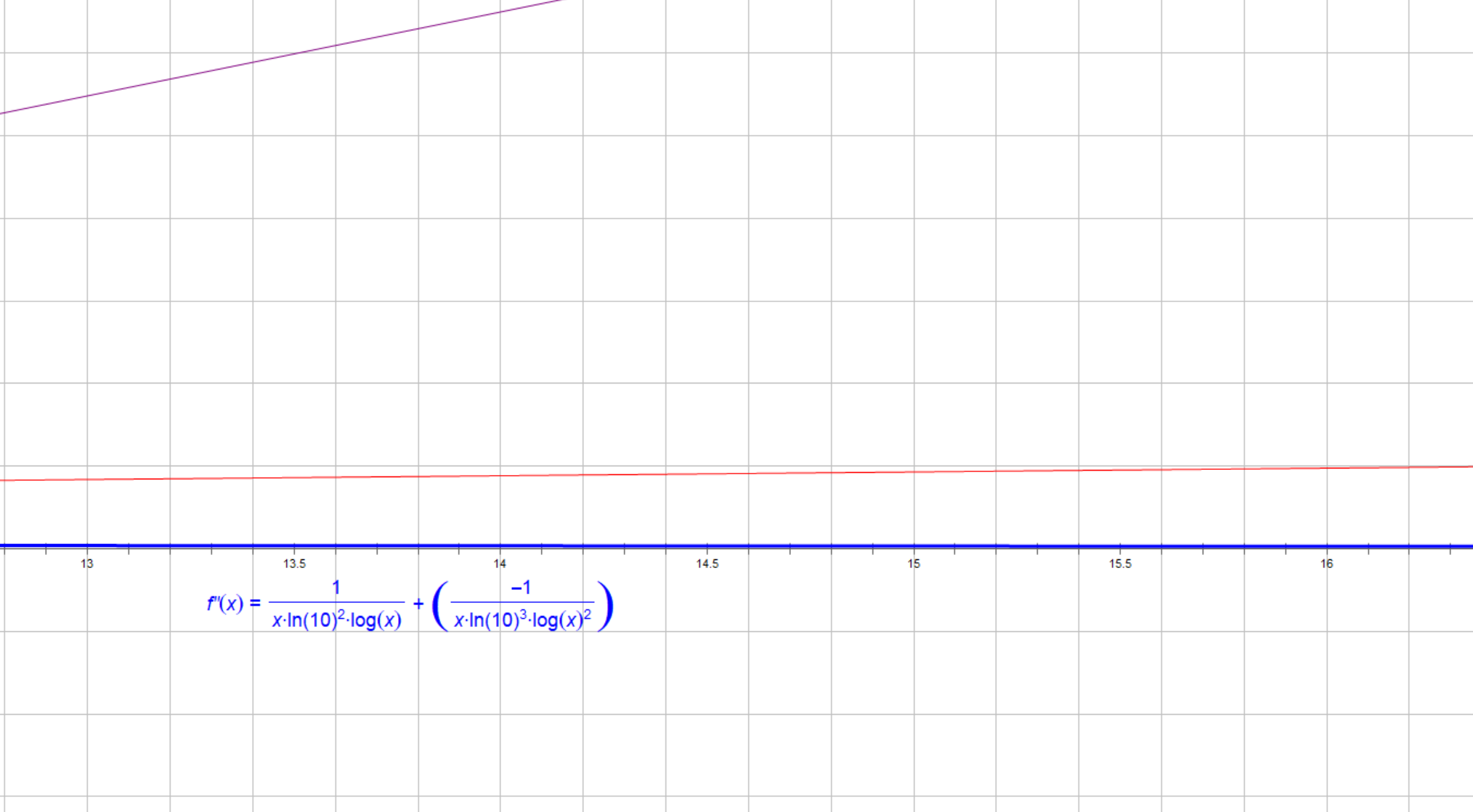
紫色:nloglogn
红色:f‘(x)
蓝色:f‘‘(x)
好了,不管那么多了,再看这次最强的筛法:欧拉筛 吧
n=3*10^7(***)
请先思考一下
为什么埃氏筛会超过线性呢?
因为其实,一个合数可能会被打上多次的合数标记
比如,枚举到2是质数的时候,会把4、6、8、10……打上标记
枚举到3是质数的时候,会把6、9、12……打上标记
然后6就被打了两次标记。
有一个更加严重的例子,一些合数甚至被打了很多次,这就浪费了很多次的机会,比如60
60这个数字被它的质因数们:2、3、5打了标记
而510510被它的质因数们:2、3、5、7、11、13、17打了标记。。。
浪费的时间就在这里了。。。
那么,欧拉筛:
#define MAXN 50000000 LL prime[MAXN]; bool book[MAXN]; LL n,size; int main() { freopen("prime.in","r",stdin); freopen("Euler.out","w",stdout); n=read(); prime[size++]=2; book[1]=1; for(re LL i=2;i<=n;i++) { if(!book[i]) prime[size++]=i,write(i); for(re LL j=0;j<size&&i*prime[j]<=n;j++) { book[i*prime[j]]=1; if(i%prime[j]==0) break; } } return 0; }
一样的套路。
首先一定要记忆化(保存prime数组)
其次无论当前的数是不是质数都要用这个数字i向后筛
但是仅仅筛到i%prime[j]==0,即i可以被从小到大的某个质数整除为止。
所以,对于一个i,第二层for仅仅会筛到它的最小质因数倍的i
即比如i=5,就只会筛走2*5,3*5,5*5(然后5%5==0 -> break;)
所以每个数只会被它的最小质因数筛——只会被筛一遍
所以它的时间复杂度是O(n)的
如果你还是不信:

#define MAXN 50000000 LL prime[MAXN]; bool book[MAXN]; LL n,size; int main() { // freopen("prime.in","r",stdin); // freopen("Euler.out","w",stdout); n=read(); prime[size++]=2; book[1]=1; for(re LL i=2;i<=n;i++) { if(!book[i]) prime[size++]=i,write(i); for(re LL j=0;j<size&&i*prime[j]<=n;j++) { book[i*prime[j]]=1; cout<<i<<" "<<i*prime[j]<<endl; if(i%prime[j]==0) break; } } return 0; }

被筛的数字是不会相同的。
咦?那这个算法1s极限怎么和高贵的埃氏筛相差无几(明明是根本一样好吧!)啊~
因为它有一定的常数(用到了取模),还一定要保存质数(这个影响不大)
但是,在更大的数据下,欧拉筛才能展现出其真正的魅力!
比如说这个数据:
200‘000‘000(2*10^8,两亿)
看上去就很不错
用埃氏筛来跑,需要3.682s左右
但是用欧拉筛,只需要2.943s左右!
(以上数据为无输出数据,且仅用于对比,无实际意义)
所以以后考试的时候还是打埃氏筛吧——又简单常数又小!
重磅出场!
标签:alt 怎么 prime 图像 记忆 book mil nlog lock
原文地址:https://www.cnblogs.com/send-off-a-friend/p/13780327.html