标签:基于 abs net inf log aop div www article
void odd_even(int n) { if(n & 1 == 1) { printf("n是奇数!\n"); } }
int swap(int x, int y) { x = x ^ y; y = x ^ y; x = x ^ y; }
基于异或运算的如下性质:
1.任意一个变量X与其自身进行异或运算,结果为0,即X^X=0
2.任意一个变量X与0进行异或运算,结果不变,即X^0=X
3.异或运算具有可结合性,即a^ b ^ c =(a ^ b)^ c = a ^(b ^ c)
4.异或运算具有可交换性,即a ^ b = b ^ a
int array[] = {1, 2, 3, 4, 5, 1, 2, 3, 4}; 采用:1 ^ 2 ^ 3 ^ 4 ^ 5 ^ 1 ^ 2 ^ 3 ^ 4; //等价于: (1 ^ 1) ^ (2 ^ 2) ^ (3 ^ 3) ^ (4 ^ 4) ^ 5; //等价于: 0 ^ 0 ^ 0 ^ 0 ^ 5; //结果为: 5;
想通过二进制解决问题,还得把数字拆成二进制来观察。比如计算m的15次方: m^15 = m^8 * m^4 * m^2 * m^1; //^表示幂运算 换成二进制: m^1111 = m^1000 * m^0100 * m^0010 * m^0001; 我们可以通过"& 1"和">> 1"来逐位读取1111,等于1时将该位代表的乘数累乘到最终结果。代码如下: int Pow(int m, int n) { int res = 1; int tmp = m; while(n != 0) { if(n & 1 == 1) { res *= tmp; } tmp *= tmp; n = n >> 1; } return res; }
int ispow(int N) { return ((N & (N - 1)) == 0) ? 1 : 0; }
int abs(int n) { return (n ^ (n >> 31)) - (n >> 31); }
int max(int x, int y) { return x ^ ((x ^ y) & -(x < y)); }
一个32bit数据的位、字节读取操作 (1)获取单字节: #define GET_LOW_BYTE0(x) ((x >> 0) & 0x000000ff) /* 获取第0个字节 */ #define GET_LOW_BYTE1(x) ((x >> 8) & 0x000000ff) /* 获取第1个字节 */ #define GET_LOW_BYTE2(x) ((x >> 16) & 0x000000ff) /* 获取第2个字节 */ #define GET_LOW_BYTE3(x) ((x >> 24) & 0x000000ff) /* 获取第3个字节 */ (2)获取某一位: #define GET_BIT(x, bit) ((x & (1 << bit)) >> bit) /* 获取第bit位 */ (3)清零某个字节: #define CLEAR_LOW_BYTE0(x) (x &= 0xffffff00) /* 清零第0个字节 */ #define CLEAR_LOW_BYTE1(x) (x &= 0xffff00ff) /* 清零第1个字节 */ #define CLEAR_LOW_BYTE2(x) (x &= 0xff00ffff) /* 清零第2个字节 */ #define CLEAR_LOW_BYTE3(x) (x &= 0x00ffffff) /* 清零第3个字节 */ (4)清零某一位: #define CLEAR_BIT(x, bit) (x &= ~(1 << bit)) /* 清零第bit位 */ (5)置某个字节为1: #define SET_LOW_BYTE0(x) (x |= 0x000000ff) /* 第0个字节置1 */ #define SET_LOW_BYTE1(x) (x |= 0x0000ff00) /* 第1个字节置1 */ #define SET_LOW_BYTE2(x) (x |= 0x00ff0000) /* 第2个字节置1 */ #define SET_LOW_BYTE3(x) (x |= 0xff000000) /* 第3个字节置1 */ (6)置位某一位: #define SET_BIT(x, bit) (x |= (1 << bit)) /* 置位第bit位 */ (7)判断某几位连续位的值 /* 获取第[n:m]位的值 */ #define BIT_M_TO_N(x, m, n) ((unsigned int)(x << (31-(n))) >> ((31 - (n)) + (m)))
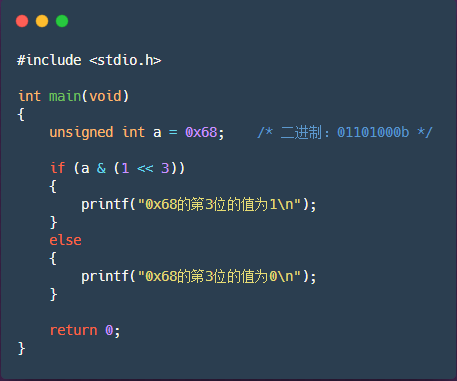
举例说明:判断0x68第3位的值。
int a=X%Y;Y必须是2^N。 公式为:a=X&(2^N-1) 或者 a=X &( ~Y);
a=a*4 改为用位操作 a=a<<2; a=a/4 改为用位操作 a=a>>2;
参考引用:
嵌入式、C语言位操作的一些技巧汇总:
https://www.cnblogs.com/zhengnian/p/11941538.html
学益得线上课堂之位运算技巧总结:
https://blog.csdn.net/xiaopengX6/article/details/104112658
标签:基于 abs net inf log aop div www article
原文地址:https://www.cnblogs.com/ggzhangxiaochao/p/13960662.html