标签:介绍 要求 还需要 解决 寻址 star 而且 数据结构和算法 这一
二叉查找树-增删查和针对重复数据处理的 Java 实现
多选参数
推荐搜索
数据结构MySQL可读代码编写javaGit
0. 前言
大家好,我是多选参数的程序锅,一个正在”研究“操作系统、学数据结构和算法以及 Java 的疯狂猛补生。本篇将带来的是二叉查找树的相关知识,知识提纲如图所示。
另外由于极客时间的《数据结构也算法之美》专栏的图太好看了,所以本篇很多地方直接使用了专栏的图片。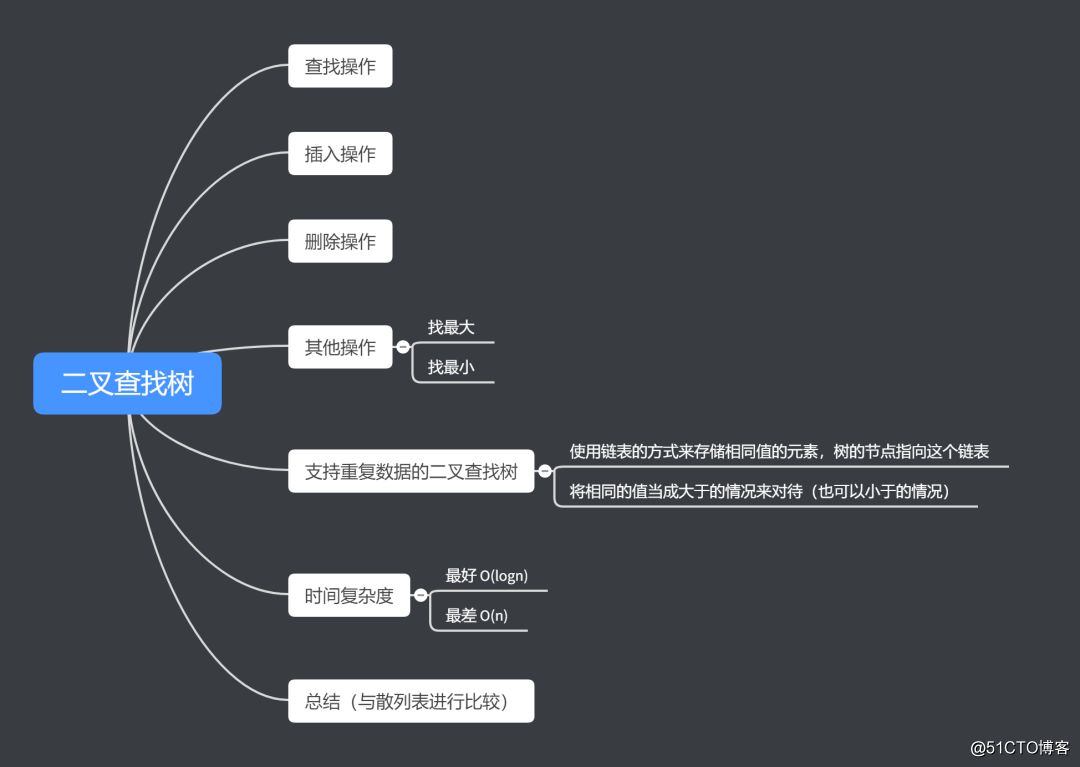
图片
1. 基本介绍
二叉查找树又名二叉搜索树又或者叫做二叉排序树,是二叉树中最常用的一种类型。二叉查找树是为了实现快速查找而生的。除了支持动态数据集合的快速查找之外,还支持动态数据集合的快速插入或删除一个数据。
之所以可以快速插入、删除、查找一个数据,是因为二叉查找树的特殊结构。二叉查找树要求树中的任何一个节点,其左子树的每个节点的值都要小于这个节点的值,而右子树的每个节点的值都大于这个节点的值。如图所示。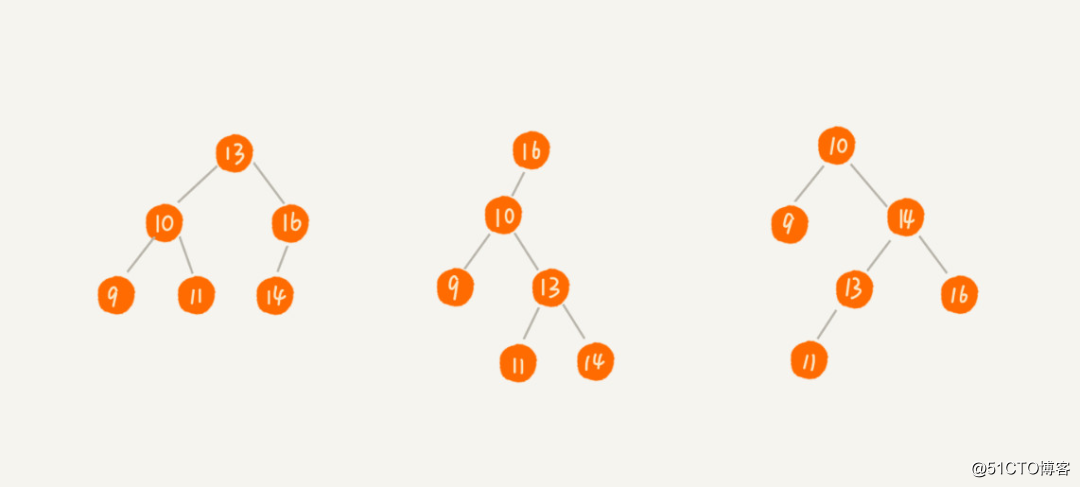
图片
2. 查找操作
先取根节点,如果根节点就等于我们要查找的数据,那就返回。如果要查找的数据比根节点要小,那么就在左子树中递归查找;如果要查找的数据比根节点的值大,那就在右子树中递归查找。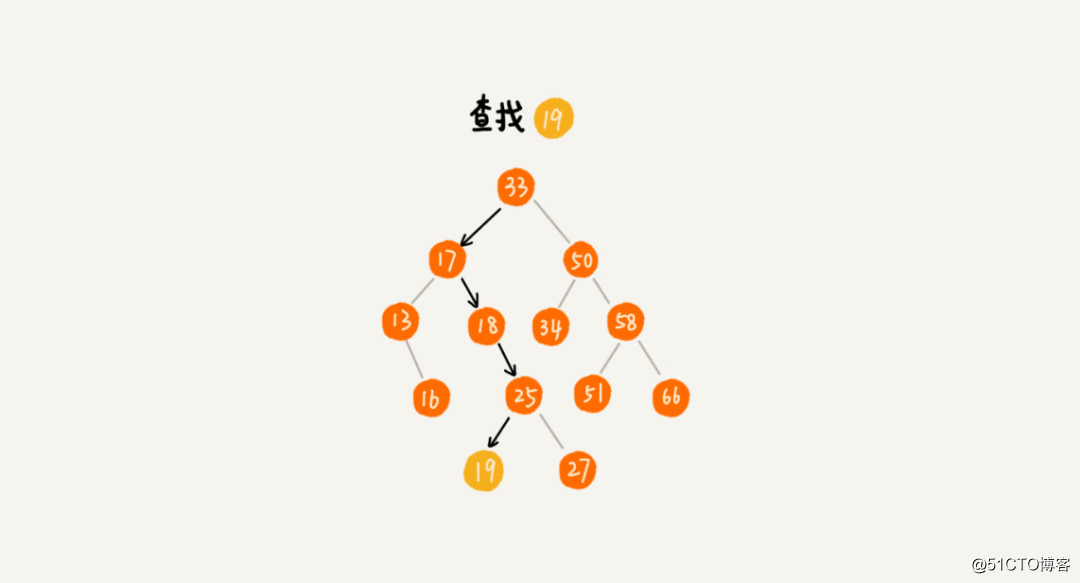
图片
实现的代码如下所示:
public Node findNode(int data) {
Node p = this.tree;
while (p != null) {
if (p.data == data) {
return p;
} else if (p.data < data) {
p = p.right;
} else {
p = p.left;
}
}
return null;
}3. 插入操作
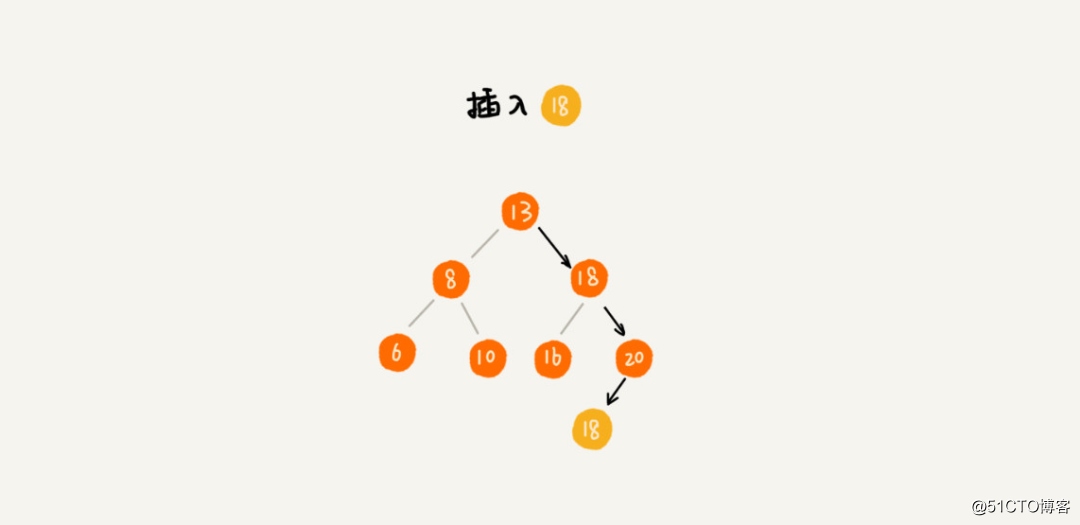
类似于查找操作,我们只需要从根节点开始,依次比较要插入的数据和节点的大小关系。这里先考虑插入数据跟已有数据不重复。如果插入的数据比节点的数据大,并且节点的右子树为空,那么直接插到右子节点的位置;如果不为空,则再递归遍历右子树,查找插入的位置。同理,如果要插入的数据比节点的数值小也是类似的。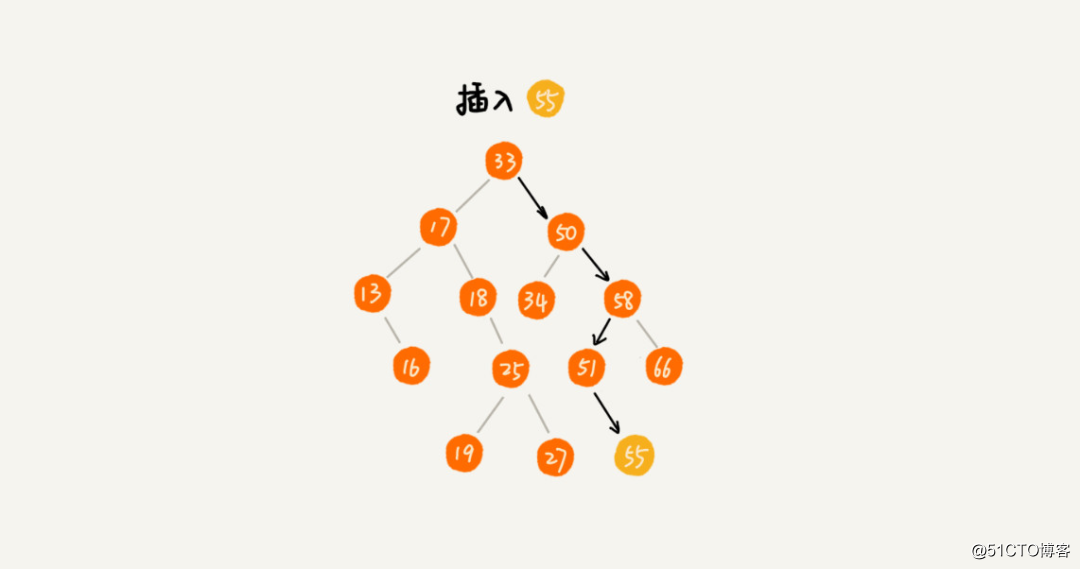
图片
实现的代码如下所示:
public void addNode(int data) {
if (this.tree == null) {
this.tree = new Node(data);
return;
}
Node p = this.tree;
while (p != null) {
if (p.data < data) {
if (p.right == null) {
p.right = new Node(data);
return;
}
p = p.right;
} else {
if (p.left == null) {
p.left = new Node(data);
return;
}
p = p.left;
}
}
}4. 删除操作
相比查找和插入操作,删除操作要繁琐的多。下面分三种情况进行讨论,当然最一开始的是先找到要删除的节点:
如果要删除的节点没有子节点,我们只需要将父节点指向要删除节点的指针置为 null。比如图中的节点 55。
如果要删除的节点只有一个子节点(左或者右),我们就可以将它的子节点更新为父节点。比如图中的节点 13。
★当然这边也可以找到左子树中的最大节点。”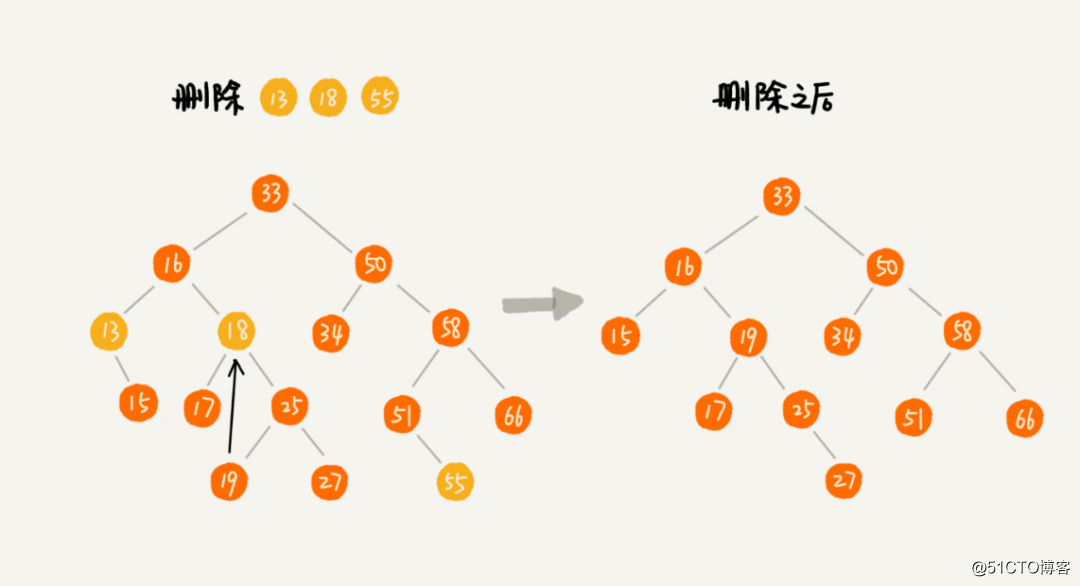
图片
实现的代码如下所示,该段代码采用了一丢丢所谓的技巧,技巧的阐述可看注释。
public void deleteNode(int data) {
Node p = this.tree;
Node pParent = null; // p 的父节点
while (p != null && p.data != data) {
pParent = p;
if (p.data < data) {
p = p.right;
} else {
p = p.left;
}
}
if (p == null) {
return;
}
// 要删除的节点有左右子节点
if (p.left != null && p.right != null) {
Node minP = p.right;
Node minPP = p; // minP 的父节点
while (minP.left != null) {
minPP = minP;
minP = minP.left;
}
p.data = minP.data; // 将 minP 的数据替换到 p 中
/* 技巧:对右子树中最小的节点进行删除,
这种情况跟要删除的节点只有一颗子树或者没有子树情况一样,
所以这边将 minPP 赋值给 pParent,minP 赋值给 p,那么重复使用一段代码 */
pParent = minPP;
p = minP;
}
Node child = null;
// 要删除的节点只有左节点的情况
if (p.left != null) {
child = p.left;
} else if (p.right != null) { // 要删除的节点只有右子节点的情况
child = p.right;
} else { // 要删除的节点左右子节点都无的情况
child = null;
}
// 删除的是根节点的情况
if (pParent == null) {
this.tree = child;
}
// 将 p 父节点的左/右子树重新指向
if (pParent.left == p) {
pParent.left = child;
} else if (pParent.right == p){
pParent.right = child;
}
}★对于二叉树的删除操作,还有一种方式就是将节点标记为“已删除”,但是又不真正地删除节点。这样会比较浪费内存空间,但是删除操作变得简单多了。并且也没有增加查找、添加操作的难度,只需要额外判断该节点是否标记为已删除。”
5. 其他操作
二叉查找树还可以支持快速查找最大节点、最小节点。除此之外,要想通过二叉查找树得到有序数据序列,只需要中序遍历二叉查找树,时间复杂度为 O(n)。所以,二叉查找树也叫二叉排序树。
public Node findMin() {
Node p = this.tree;
while (p != null && p.left != null) {
p = p.left;
}
// 这个情况相当于树为空的情况
if (p == null) {
return null;
}
return p;
}
public Node findMax() {
Node p = this.tree;
while (p != null && p.right != null) {
p = p.right;
}
if (p == null) {
return null;
}
return p;
}★前驱结点和后继节点(二叉树前驱节点和后继节点:一个二叉树中序遍历中某个节点的前一个节点叫该节点的前驱节点,某个节点的后一个节点叫后继节点)。这个操作针对一般的二叉树也有,而且一般的二叉树和二叉查找树在解决这个问题上好像并无区别。但是二叉查找树可以利用中序遍历的方式,将遍历的结果以及节点的位置保存到数组中。之后通过索引值 +1,-1 的方式即可访问到前驱节点和后继节点。一般方式可参考:https://www.cnblogs.com/xiejunzhao/p/f5f362c1a89da1663850df9fc4b80214.html”
★完整的代码可查看 github 仓库 https://github.com/DawnGuoDev/algos ,这个仓库将主要包含常用数据结构及其基本操作的手写实现(Java),也会包含常用算法思想经典例题的实现(Java)。在接下来一年内,这个仓库将会保持更新状态,在此之间学到的关于数据结构和算法的知识或者实现也都会往里面 commit,所以赶紧来 star 哦。”
6. 支持重复的数据的二叉查找树
前面实现的代码都是直接存储数组并且不存在重复数据的前提下实现的,那么二叉树要存储对象的话,那么可以以对象的 key 来构建二叉查找树。同时,考虑存在重复 key 值并且可同时存储的情况,可以采用这么几种方法进行解决。
第一种,二叉查找树中每个节点不单单存储一个数据,而是存储一个链表的首地址等,那么把相同的数据都存储在该链表上,这样就相当于把值相同的数据都存储在同一个节点上了。
图片
当要查找数据的时候,遇到值相同的节点,并不停止查找,而是继续在右子树中查找,直到遇到叶子节点才停止。这样就可以把键值等于要查找值的所有节点都找出来。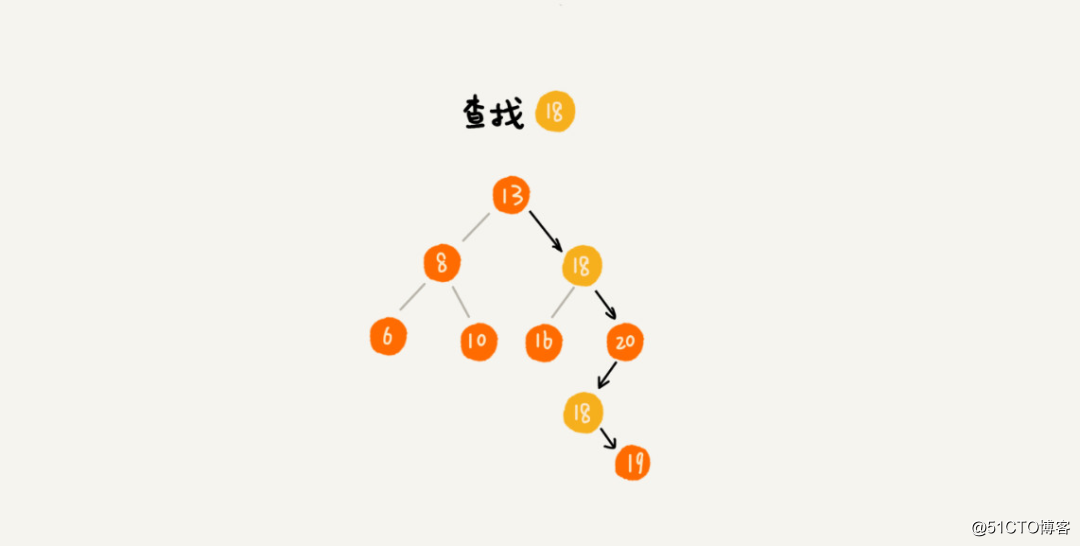
图片
对于删除操作,也需要先查找到每个要删除的节点,然后再按前面讲的删除操作的方法,依次删除。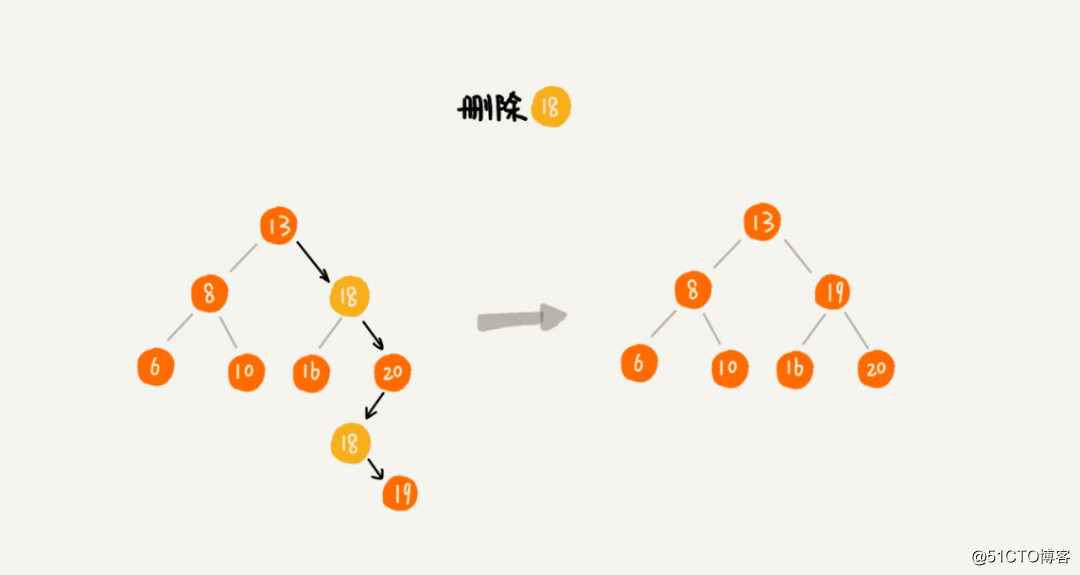
图片
★关于重复数据操作的代码可查看 github 仓库 https://github.com/DawnGuoDev/algos ,这个仓库将主要包含常用数据结构及其基本操作的手写实现(Java),也会包含常用算法思想经典例题的实现(Java)。在程序锅找到工作之前,这个仓库将会保持更新状态,在此之间学到的关于数据结构和算法的知识或者实现也都会往里面 commit,所以赶紧来 star 哦。”
7. 二叉查找树的时间复杂度
针对同一组数据,可以构造出不同形态的二叉查找树。比如下图就根据同一组数据构造出了不同形态的二叉查找树。显然,查找、插入、删除的时间复杂度跟二叉树数据的形态有关系。具体地说,时间复杂度跟树高度有关系。比如在最左边的那棵二叉查找树中查找数据时,相当于在链表中查找数据,时间复杂度为 O(n);在最右边的那棵二叉查找树查找时(完全二叉树的情况),时间复杂度是最小的,为 O(logn)。
★这里对完全二叉树的高度进行计算。完全二叉树中,第一层有 1 个节点,第二层有 2 个节点,第三层有 2^2 节点,第 k 层有 2^(k-1) 节点。假设一棵 n 个节点的完全二叉树有 k 层,那么第 k 层可能是 1 个节点,也可能是 2^(k-1) 个节点。进一步地,n 介于 1 + 2 + ... + 2^(k-2) + 1 和 1 + 2 + ... + 2^(k-1) 之间。推到得,k 介于[log_2^(n+1), (log_2^n)+1],也就是说完全二叉树的层数小于等于 log_2^n+1。因此,时间复杂度为 O(logn)。”
★对于二叉查找树的时间复杂度为 O(logn) 还有另一种理解方式,那就是二叉查找树查找的思想和二分查找的思想是类似的,都是每次查找之后取一半。因此,这两者的时间复杂度都是 O(logn)。”
虽然二叉查找树的时间复杂度可以达到 O(logn),但是一旦出现不平衡的情况就会退出的特别严重,可能退化为 O(n)。显然,不平衡的二叉查找树是我们不希望遇到的,我们希望在任何时候,都能保持二叉查找树的平衡。因此有了平衡二叉查找树,平衡二叉查找树的高度接近 logn。所以查找、删除、插入操作的时间复杂度也比较稳定,都是 O(logn)。
在平衡二叉查找树中,比较苛刻的有 AVL 树,不那么苛刻的有红黑树,而红黑树在生活中被用的更多。
8. 总结
散列表的插入、删除、查找操作的时间复杂度可以做到常量级 O(1),而二叉查找树在比较平衡的情况下(平衡二叉查找树),插入、删除、查找操作的时间复杂度才是 O(logn)。在时间复杂度上,平衡二叉查找树相对来说并不是优势。但是平衡二叉查找树相比散列表有这么几个优势,这几个优势导致平衡二叉查找树还是优于散列表的。但是在实际的开发过程中,还是需要根据实际需求来进行选择。
散列表中的数据是无序存储的,如果要输出为有序的数据,还需要先进行排序(不考虑再使用一个链表的情况)。而对于平衡二叉查找树,只需要进行中序遍历,即可在 O(n) 的时间复杂度内,输出有序的数据序列。
散列表需要扩容,扩容会耗时很多,而且当遇到散列冲突时,性能不稳定。虽然二叉查找树也不稳定,但是常用的平衡二叉查找树的性能还是很稳定的,时间复杂度稳定在 O(logn)。
从复杂度上来说,散列表的查找等操作的时间复杂度是常量级,但是因为哈希冲突的存在,这个常量不一定比 logn 小。所以实际的查找速度可能不一定比 O(logn) 快。而且散列表的哈希函数还需要耗时(我们在分析散列表的时间复杂度时是将哈希函数的计算当做常量的),所以更不一定就比平衡二叉查找树的效率高。
散列表的构造要比二叉查找树更复杂,需要考虑的东西很多,比如散列函数的设计、冲突方法的选择、扩容策略的选择以及装载因子的权衡等。而平衡二叉查找树只需要考虑平衡性这一个问题,而且平衡性的解决方案已经比较成熟、固定了。
散列表为避免过多的散列冲突,装载因为不能太大。尤其在采用了开放寻址法解决冲突的散列表中,装载因子不能太大,从而导致浪费一定的存储空间。
9. 巨人的肩膀
极客时间专栏,王争老师的《数据结构也算法之美》
10. 附 Github
整个系列的代码可查看 github 仓库 https://github.com/DawnGuoDev/algos ,这个仓库将主要包含常用数据结构及其基本操作的手写实现(Java),也会包含常用算法思想经典例题的实现(Java)。在接下来一年内,这个仓库将会保持更新状态,在此之间学到的关于数据结构和算法的知识或者实现也都会往里面 commit,所以赶紧来 star 哦。
不甘于「本该如此」,「多选参数 」值得关注
标签:介绍 要求 还需要 解决 寻址 star 而且 数据结构和算法 这一
原文地址:https://blog.51cto.com/15054039/2563121