标签：void   分解   图片   turn   print   不重复   http   target   资料   

什么是回溯算法

回溯算法本质就是枚举，在给定的枚举集合中不断从其中尝试搜索找到问题的解，如果在搜索过程中发现不满足求解条件，则回溯返回，尝试其他路径继续搜索解决，这种走不通就回退再尝试其他路径的方法就是回溯法。

回溯算法解题通用套路

解决一个回溯问题，实际上就是一个决策树的遍历过程。你只需要思考3个问题：

1. 路径：也就是已经做出的选择。
2. 选择列表：也就是你当前可以做的选择。
3. 结束条件：也就是到达决策树底层，无法再做选择的条件。

通用解决方案伪代码

result = []
function backtrack(路径, 选择列表) {
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择
}

它一般是解决树形问题的，问题分解成多个阶段，每个阶段有多个解，这个就构成了一颗树，所以判断问题是否可以用回溯算法的关键在于它是否可以转成一个树形问题。
另外我们也发现如果能够缩小每个阶段的可选解，就能让问题的搜索规模都缩小，这种叫做剪枝，通过剪枝能有效降低整个问题的搜索复杂度。

回溯算法解决全排列问题

我们在高中的时候就做过排列组合的数学题，我们也知道 n 个不重复的数，全排列共有 n! 个。
那么我们当时是怎么穷举全排列的呢？比方说给三个数 [1,2,3]，你肯定不会无规律地乱穷举，一般是这样：

先固定第一位为 1，然后第二位可以是 2，那么第三位只能是 3；然后可以把第二位变成 3，第三位就只能是 2 了；然后就只能变化第一位，变成 2，然后再穷举后两位……

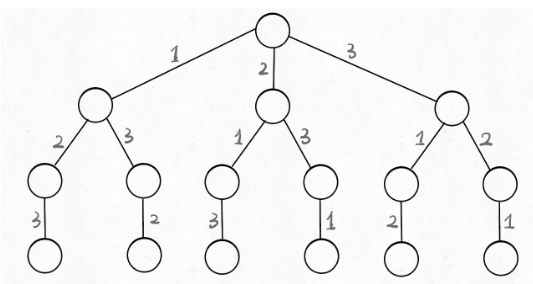
其实这就是回溯算法，我们高中无师自通就会用，或者有的同学直接画出如下这棵回溯树：

public class Test {

    public static void main(String[] args) {
        Test test = new Test();
        int[] nums = {1, 2, 3};
        System.out.println(test.permute(nums));
    }

    public List<List<Integer>> permute(int[] nums) {
        if (nums == null || nums.length == 0) {
            return Collections.emptyList();
        }

        List<List<Integer>> result = new ArrayList<>();
        backtrack(result, new ArrayList<>(), nums);

        return result;
    }

    private void backtrack(List<List<Integer>> result, List<Integer> selectNums, int[] allNums) {
        if (selectNums.size() == allNums.length) {
            result.add(new ArrayList<>(selectNums));
            return;
        }

        for (Integer num : allNums) {
            // 剪枝
            if (selectNums.contains(num)) {
                continue;
            }

            selectNums.add(num);
            backtrack(result, selectNums, allNums);
            selectNums.remove(num);
        }
    }

}

参考资料

• https://zhuanlan.zhihu.com/p/93530380

回溯算法

标签：void   分解   图片   turn   print   不重复   http   target   资料   

原文地址：https://www.cnblogs.com/powercto/p/14220257.html