标签:冲突 很多 att ring for 内容 info 不同的 amp
在字符串中肯定会遇到顶顶有名的KMP算法,下面让我们一起回顾一下吧~
什么是KMP?
KMP是由Knuth,Morris和Pratt这三位学者发明的一种算法,所以取了三位学者名字的首字母。主要应用于字符串匹配问题上。假如文本串aabaabaaf的长度为n,模式串aabaaf的长度为m,我们要判断文本串中是否包含该模式串,传统的解决方法是在文本串中遍历模式串,如果遇到不匹配的字符了则又要从文本串下一位再从头遍历。时间复杂度为O(m*n)。而KMP的思想在于:「当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,避免从头再去做匹配了。」时间复杂度为O(m+n)。所以KMP算法极大的提高了搜索效率。
前缀表
要想了解KMP算法,首先得知道什么是前缀和后缀以及最长相等前后缀。举个栗子??:
对于字符串aabaaf来说,它的前缀有a,aa,aab,aaba,aabaa即除了最右端字符所组成的集合,同理它的后缀有f,af,aaf,baaf,abaaf即除了最左端字符所组成的集合。在模式串aabaaf的所有字串中
"a"的前缀和后缀都为空集,最长相等前后缀长度为0;
"aa"的前缀为[a],后缀为[a],最长相等前后缀长度为1;
"aab"的前缀为[a, aa],后缀为[b, ab],最长相等前后缀长度为0;
"aaba"的前缀为[a, aa, aab],后缀为[a, ba, aba],最长相等前后缀长度为1;
"aabaa"的前缀为[a, aa, aab, aaba],后缀为[a, aa, baa, abaa],最长相等前后缀长度为2;
"aabaaf"的前缀为[a, aa, aab, aaba, aabaa],后缀为[f, af, aaf, baaf, abaaf],最长相等前后缀长度为0;
可以看到这里得到了一个序列,也就是大家所熟悉的next[]数组。即该模式串aabaaf的next[]数组为[0,1,0,1,2,0],这也就是前缀表。
为什么要用到前缀表呢?
因为前缀表主要是用来回溯的,记录了模式串与文本串不匹配的时候,模式串应该从哪开始匹配。
如图所示:
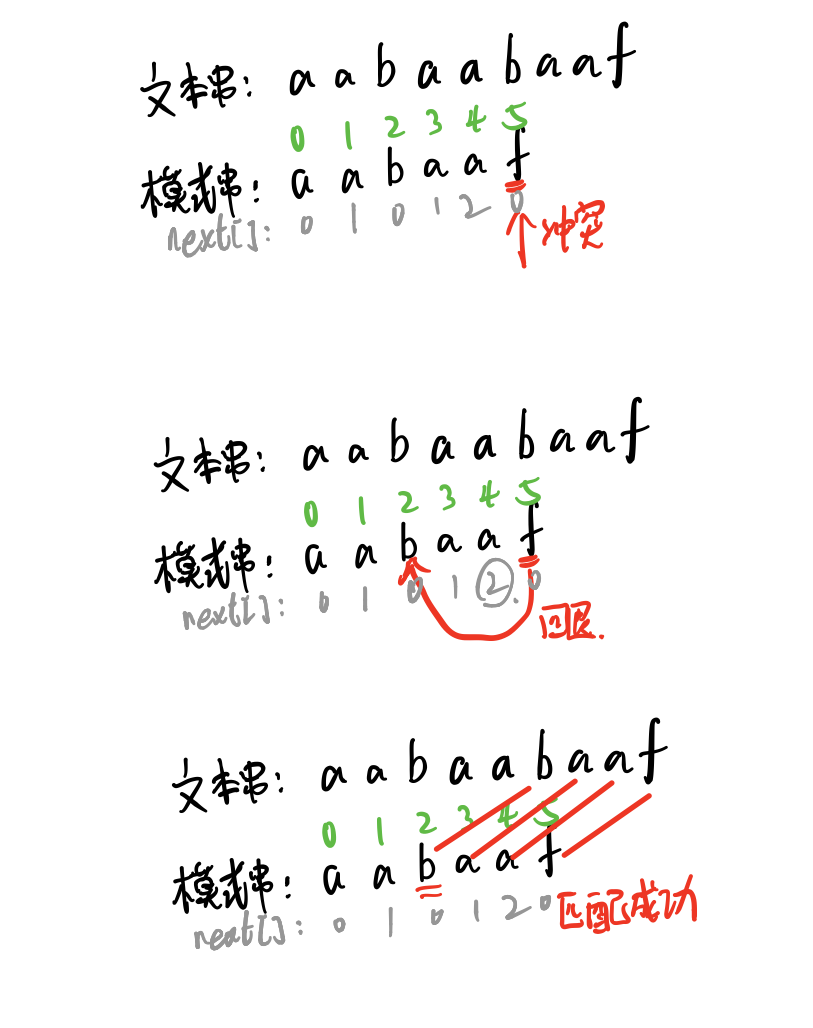
这里面的回退跳转靠的就是前缀表(next[]数组)。字符串在字符f发生冲突时,就回退到f前一位next[]数组中的值所指向的位置处,也就是回退到2再进行匹配。
可能很多同学看到的next[]数组是全部统一减一操作或者是右移首位补上-1。其实本质都是一样的,回退到应该回退的位置,只不过修改了判断条件。
模式串aabaaf的next[]数组三种如下,以及对应的回退方式。

求解next[]数组
主要包括四个步骤:
/推荐这种/
//当前字符串冲突时回退到前一位next数组对应的值
/*
i:指向后缀末尾
j:指向前缀末尾,也代表包括i在内的之前的最长相等前后缀的长度
*/
func getNext(next []int, s string) {
//初始化
j := 0
next[0] = 0
for i := 1; i < len(s); i++ {
//前后缀不相同的情况
for j > 0 && s[i] != s[j] {
j = next[j-1] //回退
}
//前后缀相同的情况
if s[i] == s[j] {
j++
}
next[i] = j
}
}
next[]数组全部统一减一操作的代码如下:
//统一减一操作
func getNext(next []int, s string) {
//初始化
j := -1
next[0] = -1
for i := 1; i < len(s); i++ {
//前后缀不相同的情况
for j >= 0 && s[i] != s[j+1] {
j = next[j]
}
//前后缀相同的情况
if s[i] == s[j+1] {
j++
}
next[i] = j
}
}
标签:冲突 很多 att ring for 内容 info 不同的 amp
原文地址:https://www.cnblogs.com/zmk-c/p/14409513.html