标签:字符串匹配 task hot 怎么 子串 实践 tps media 生成
KMP算法主要用于查找字符串,是 D.E.Knuth、J,H,Morris 和 V.R.Pratt 三位神人共同提出的,称之为 Knuth-Morria-Pratt 算法,简称 KMP 算法。该算法相对于 Brute-Force(暴力)算法有比较大的改进,主要是消除了主串指针的回溯,从而使算法效率有了某种程度的提高。
讲KMP算法之前,我们要先讲暴力算法
暴力算法就是在一段文字中一个一个的匹配字符串,匹配不成功从头开始匹配
例如,从下图文字中找到"ABCABCD"


匹配第七个字符’D’时,没匹配到,继续从第二个位置重新开始匹配

匹配第一个字符’A’时,没匹配到,继续从第三个位置重新开始匹配

匹配第一个字符’A’时,没匹配到,继续从第四个位置重新开始匹配

匹配第七个字符’D’时,没匹配到,继续从第五个位置重新开始匹配
总共要匹配17次
int ViolentMatch(string text, string pattern) //text是文本串,pattern是关键字
{
int tLen = text.size();
int pLen = pattern.size();
int i = 0;
int j = 0;
while (i < tLen && j < pLen)
{
if (text[i] == pattern[j])
{
//如果当前字符匹配成功(即text[i] == pattern[j]),匹配下一个字符
i++;
j++;
}
else //如果当前字符匹配失败,pattern从头开始匹配
{
i = i - j + 1;
j = 0;
}
}
if (j == pLen) //当pattern全部匹配成功,返回匹配位置
return i - j;
else
return -1;
}
每次匹配字符串失败后都要回从头开始匹配,如果文本串的长度是n,关键字的长度是m,那么算法效率(最差)就是n*m
以上内容来自:3月24日白羊座的csdn博客,感谢!
解读KMP之前,我们先来理解一下KMP算法存在的理由。对于模式匹配,目前所学的最简单的是BF算法,即偏向于“暴力”匹配的方法。另外一种就是较为复杂KMP算法了。而俩者的区别在于:BF算法是时间复杂度相对高的,KMP则可以理解为用空间换时间。
暴力算法:逐个匹配主串字符,然后模式串j值回溯到1重新匹配。
KMP算法: KMP只需要将j值模式串中j的位置回溯到next[j]位,而免除了前面不需要的匹配,以此来换取时间。
相比一个一个比较,而KMP则在此基础上更加的简便了。
接下来,我们来用有逻辑的语言来了解KMP算法。而后,再解释如何用代码实现该算法。
首先,我们从代码的实现效果来看,主串与模式串每次历往KMP算法,模式串中移动至K位与失配的(主串)的i位对其,而不需要像BF算法一样,一次次回溯从头开始。
OK,我们现在什么废话都不讲。先前的直播中我们多次提到了next数组。我们都不管他长什么样存的是什么东西了,直接上实践例子。
给你文本:
"BBCABCDABABCDABCDABDE"
待匹配文本:
"ABCDABD"
和一个next数组
next[] = {0,0,1,1,2,0,1,2,3,4,5}
再给你一个公式:
移动位数 = 已匹配值 - 部分匹配值 (其实就是直接从最长前缀直接跳到与他相等的最长后缀那里开始往后匹配)
(说人话:移动位数 = 已匹配值 - 最大公共元素长度)
现在我一步一步模拟一下KMP匹配的过程
1.第一步匹配与暴力没有区别,找到第一个都是A的点开始匹配:
可以看到,我们匹配到第6位的时候,匹配失败了,我们直接中断本次匹配
然后移动 已匹配值 - 最大公共元素长度 位
我们匹配了5位,对应的next[5] = 2,那么我们就应该移动 5 - 2 = 3位。
结果如下:
很好,我们现在又可以进行匹配了,匹配到第11位时,又匹配失败了,我们同样中断本次匹配并进行移动操作。
如图: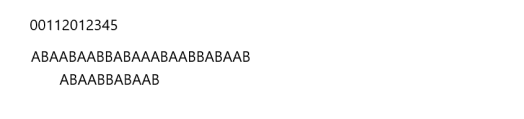
继续套公式,我们需要移动已匹配值 - 最大公共元素长度 位
我们匹配了10位,对应的next[10] = 4,那么我们移动10-4 = 6位,结果如下: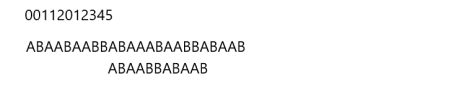
如法炮制,我们继续进行匹配,匹配到第5位的时候又出错了,继续进行处理: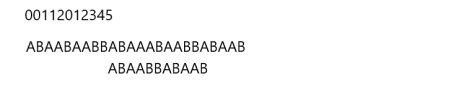
移动已匹配值 - 最大公共元素长度 位
我们匹配了4位,对应next[4] = 1,我们需要移动4 - 1 = 3 位。
结果:
这次拉跨了,只匹配到了1位...... 但我们依然要继续操作~
移动已匹配值 - 最大公共元素长度 位
这次匹配了1位,对应next[1] = 0,我们要移动 1 - 0 = 1 位
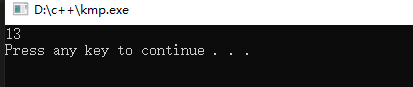
很好!我们这次可算是匹配上了,至此,一次KMP字符串匹配操作就完成了,跑一下程序,我们是在文本的第
下标处完成的匹配,自己验证一下看是否正确吧
(当然是正确的啦!不过还是提一下:next数组我们是从1开始计数,text文本是从0开始计数)
对应上面这个例子,有动图可以看,不过我觉得不是很清晰,还是自己手做了模拟
现在知道next数组的作业和kmp算法的查找过程了吧。那么很明显,在kmp算法中最重要的部分就是
next[] 数组。它存放的是我们当前位置下的最大公共元素长度
(说人话:我也不知道该怎么说了,直接给大家模拟一下这个数组内的值是怎么来的吧)
我之前有说过:前缀,后缀,其实非常简单的两个概念。
我们还是拿一个待匹配文本
"ABCDABD"来说事
我直接上图,大家就可以看懂咯~
看懂了吗?前缀后缀就是:把字符串的子串分解出来,从前到后(前缀),从后到前(后缀)的一个排列
!注意:(前缀得不最后一位,后缀得不到最前一位,看图理解!)
然后我们找出前缀和后缀中相同的子排列,将它们的长度保存到字符串子串的长度下的下标中去(就是第一列字符串的长度做下标)
这也可以很浅显的让大家理解,为什么next数组计数是从1开始的了吧~
另外,大家应该发现了next数组是对待匹配文本的处理吧
所以next数组的长度应该 = 待匹配文本的长度
只要我们求出next数组,就可以愉快的进行KMP字符串匹配咯
来,检验一下你能否自己独立模拟出来整个KMP的过程~
给你文本:"BBCABCDABABCDABCDABDE"
待匹配文本:"ABCDABD"
还有上图已经给出了的next数组:next[] = {0,0,0,0,1,2,0}
请你现在手动画图模拟一下过程,然后再来跟我的程序对一下答案(如果找到了,请输出匹配处的下标,否则请输出-1)
不要偷偷看哦~
芜湖!答案还是13~,模拟对了吗?
KMP算法由两部分组成
首先是对待匹配文本的处理——生成next数组
其次才是进行kmp匹配的模拟。
c++代码如下:
#include <bits/stdc++.h>
using namespace std;
//在关键字中记录与前缀匹配的组合,记录在next数组
void make_next(string pattern, int *next)
{
int q, k; //q是匹配的位置,k是前缀开始的地方
int m = pattern.size(); //关键字的长度
next[0] = 0; //用于记录关键字中与前缀匹配的组合的位置
for (q = 1, k = 0; q < m; q++)
{ //q是后面的数,k是前缀开始的地方
while (k > 0 && pattern[q] != pattern[k])
{ //当后面的组合与前缀不同时,前缀数-1继续匹配
k = next[k - 1];
}
if (pattern[q] == pattern[k])
{ // 如果前缀与后面有相同字符
k++;
}
next[q] = k; //用于记录关键字中与前缀匹配的组合的位置
}
}
//kmp算法
int kmp(string text, string pattern, int *next)
{
int n = text.size(); //文本串的长度
int m = pattern.size(); //关键字的长度
make_next(pattern, next); //在关键字中记录与前缀匹配的组合,记录在next数组
int i, q;
for (i = 0, q = 0; i < n; i++)
{ //i --> text, q --> pattern
while (q > 0 && pattern[q] != text[i])
{ //如果匹配失败,往前找与前缀相同组合的位置
q = next[q - 1]; //只要next[q-1]不大于0,那么就是还没找到与前缀相同的组合
} //继续在循环中找到与前缀相同的组合,直到next[q-1]等于0
if (pattern[q] == text[i])
{ //如果匹配正确,关键字位置+1
q++;
}
if (q == m)
{ //如果q的位置是关键字的长度,那么就是找到字符串了
return i - q + 1; //返回字符串的位置
}
}
return -1; //整个文本串找完都没有找到字符串,返回-1
}
int main()
{
string text = "ABAABAABBABAAABAABBABAAB";
string temp = "ABAABBABAAB";
int len = temp.size();
int arr[len+1];
make_next(temp, arr);
cout << kmp(text, temp, arr);
return 0;
}我把一些细节都写在了注释内,请大家细品。
(另外我也手写不出来,查找了一下资料才写出来的哈哈。)
最后感谢这两篇博客对我的启发,让我能写下这篇博客~
长臂人猿- 通俗易懂的KMP算法详解(严蔚敏版C语言)
3月24日白羊座 - KMP算法(看一遍解决)
挺晚的了,晚安~
标签:字符串匹配 task hot 怎么 子串 实践 tps media 生成
原文地址:https://www.cnblogs.com/cherryg/p/14474463.html