【python】Leetcode每日一题-存在重复元素3

标签：else   关系   get   描述   个数   很多   return   target   solution   

【python】Leetcode每日一题-存在重复元素3

【题目描述】

给你一个整数数组 nums 和两个整数 k 和 t 。请你判断是否存在 两个不同下标 i 和 j，使得 abs(nums[i] - nums[j]) <= t ，同时又满足 abs(i - j) <= k 。

如果存在则返回 true，不存在返回 false。

示例1：

输入：nums = [1,2,3,1], k = 3, t = 0
输出：true

示例2：

输入：nums = [1,0,1,1], k = 1, t = 2
输出：true

示例3：

输入：nums = [1,5,9,1,5,9], k = 2, t = 3
输出：false

提示：

0 <= nums.length <= 2 * 10^4
-2^31 <= nums[i] <= 2^31 - 1
0 <= k <= 10^4
0 <= t <= 2^31 - 1

【分析】

• ??又学到了很多东西，有时间把前面的都归纳一下吧

• 思路1：桶排序

  对于这题，我们可以以(t+1)长度为一个桶，num/(t+1)为桶号，则例如0、1、2、···、t为一个号为0的桶，-1、-2、···、-t、-(t-1)为一个号为-1的桶，由此利用哈希表可以记录存在元素的桶号，同时维护哈希表长度为k，则可以控制哈希表内元素为nums上连续k个元素。

  在遍历nums时，如果对于一个元素对应的桶号在哈希表内已存在，则返回True，同时还有一种情况，因为桶容量构造为(t+1)，可能存在相邻桶在哈希表中，如，t与t+1分别在0号和1号桶，而它们满足题设不等式关系，因此同时还需检查是否存在相邻桶以及其中元素是否满足关系，（由于需要检查其中桶号对应元素值，所有需要map数据结构。

• 代码

class Solution:
    def containsNearbyAlmostDuplicate(self, nums: List[int], k: int, t: int) -> bool:
        def getIdx(u):
            return (u+1) // size - 1 if u < 0 else u // size
        
        map = {}
        size = t + 1
        for i,u in enumerate(nums):
            idx = getIdx(u)
            # 目标桶已存在（桶不为空），说明前面已有 [u - t, u + t] 范围的数字
            if idx in map:
                return True
            # 检查相邻的桶
            l, r = idx - 1, idx + 1
            if l in map and abs(u - map[l]) <= t:
                return True
            if r in map and abs(u - map[r]) <= t:
                return True
            # 建立目标桶
            map[idx] = u
            # 维护个数为k
            if i >= k:
                map.pop(getIdx(nums[i-k]))
        return False

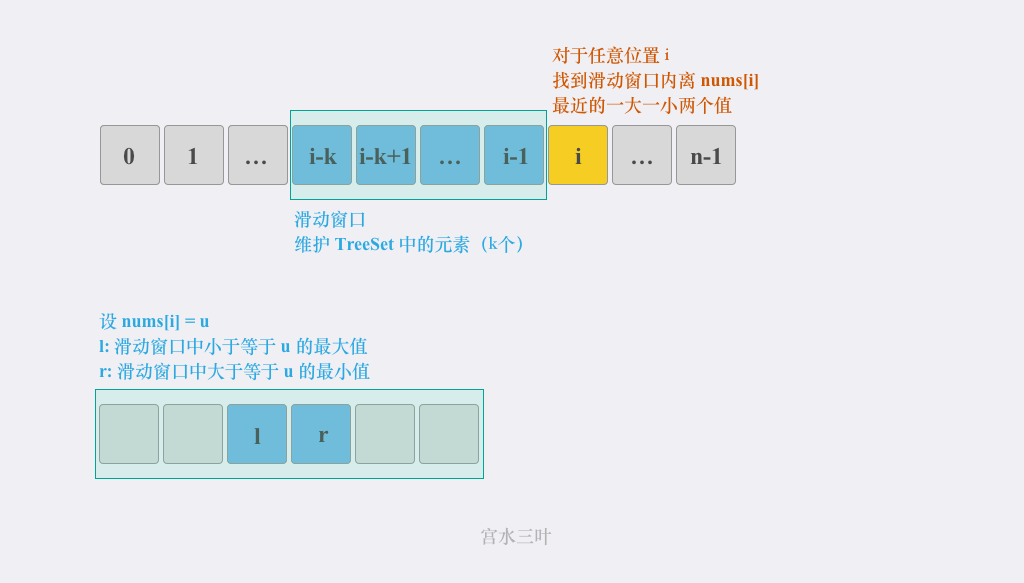
• 思路二：滑动窗口

  滑动窗口，其实就是遍历nums每个元素，每个元素检查其前k个元素，而这k个元素则很像一个窗口，遍历元素即为窗口滑动。

  而仅有滑动窗口时间复杂度为\(O(nk)\)，在leetcode上会TLE，因此需要优化，比如加入对前k个元素的二分查找，或者有序化，来维护前k个元素。

  

  参考链接

【python】Leetcode每日一题-存在重复元素3

标签：else   关系   get   描述   个数   很多   return   target   solution   

原文地址：https://www.cnblogs.com/krnl-dpr/p/14672622.html