标签:computer eric not 报告 下载 eal versions execution 计算机
【概述】
有限状态机(有时称为有限状态自动机)是一种可以用硬件或软件实现的计算模型,可以用来模拟顺序逻辑和某些计算机程序。
有限状态自动机生成常规语言。它可用于对许多领域的问题进行建模,包括数学,人工智能,游戏和语言学。
【米里状态机 Mealy State Machine】
顺序系统,其中输出取决于当前输入和状态
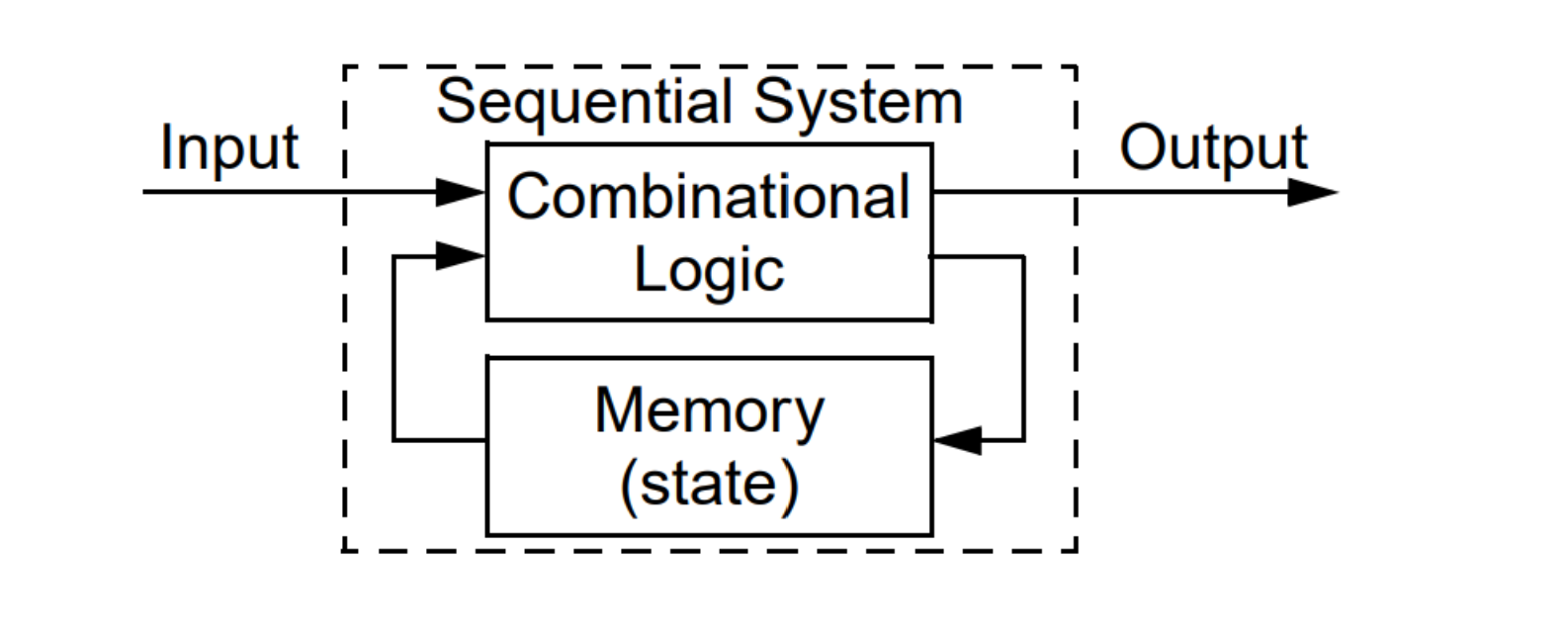
有限状态机(FSM)对正则表达式提供了不同的观点,一个FSM描述了一个正则表达式的行为,每个FSM由以下5个元组成
Q: 有限的状态集 a finite set of states
Σ: 有限的字母集 a finite alphabet set 针对某些状态采用的action
δ: Q X Σ → Q: 转换函数/映射函数 一组从状态和输入到状态的映射 transition function -a set of maps from states and inputs into states 在某个状态下采用某个action而得到新状态的转化
q0: 初始状态 an initial state (q0 ∈Q)
F: 一组最终/接受状态a set of final/accepting states (F ?Q)
每个FSM可能有不同的状态集、字母集、映射函数、初始与最终状态,针对不同的情况,我们会有不同的FSM的设计(不同问题,不同设计)
FSM是抽象机,在任何给定时间只能处于有限数量的状态(Q)之一。
FSM可以响应某些外部输入而从一种状态转换为另一种状态
【状态 States】
状态集通常描述机器的当前状态。机器的当前状态通常取决于机器的先前状态,总有如下两种特殊状态
1.起始状态 Start State : FSM始终在此状态下开始。起始状态通常用箭头“从任何地方指向它”表示。一般会在它的圆圈上加上三角形来表示它
2.完成状态 Finish State(s) : 如果要识别该语言,则FSM必须在此状态(或其中一种状态)下完成。完成状态是机器报告接受输入的状态。接受状态通常用双圆圈表示
所有其他状态都被视为中间状态。通常使用qx表示状态,其中x是某个数字
【字母与转换函数 Alphabet & Transition Functions】
字母表 Alphabet :字母描述了机器可接受的输入
转换函数 Transition Functions :任何状态和字母符号的转换函数都是要转换成的一个或多个下一个状态,转换由上方带有字母符号的箭头表示
例子:比如现在有q0,q1,q2,q3三种状态,其中q0是初始状态(圆圈+三角形)、q3是最终状态(双圆圈),它们之间有a、b两种转化方式(箭头表示转化)
比如我们在q0的状态接受到了a,那么便会转换到q1
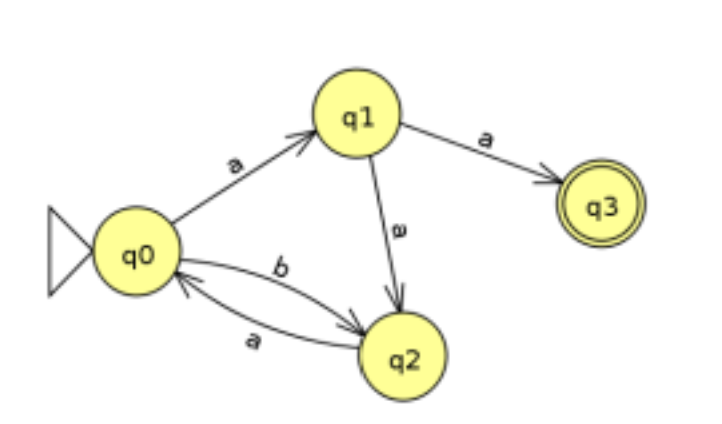
状态集是:{q0,q1,q2,q3}
字母集是:{a,b}
【转换表 Transition Table】
一个FSM可以用一个表来表示。这个表将包含状态、字母和转换,例如上面的例子,我们可以用下图来表示
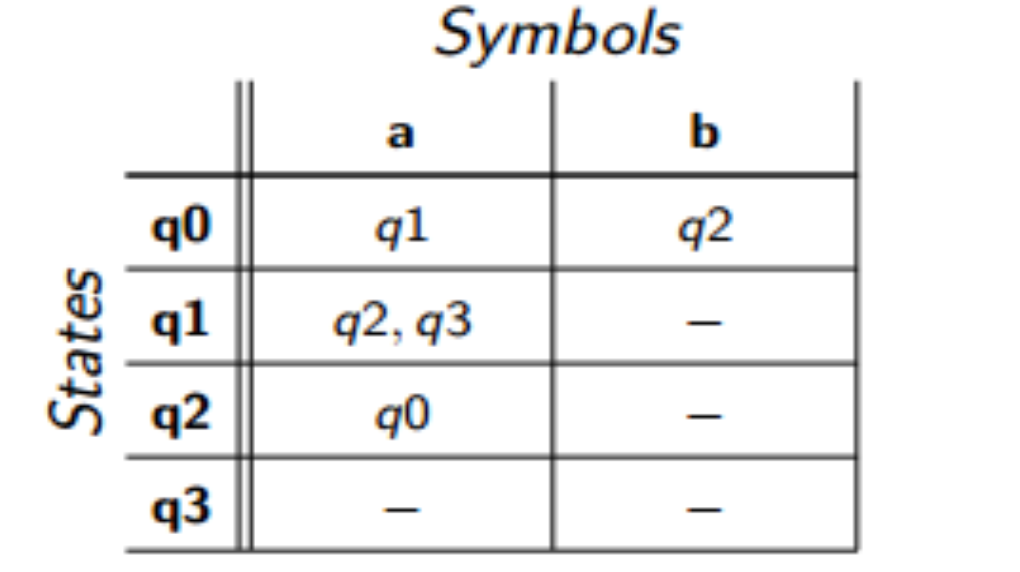
【词典顺序 Lexicographical Ordering】
当枚举字母表中所有可能的字符串时,我们以字典顺序显示它们。
这意味着首先列出较短的字符串,而对于长度相同的字符串,则以字母alphabetical或数字numerical顺序表示
比如给定一个字母表 Σ= {??,??},列出L中所有长度小于四的字符串,其中L是所有可能的由Σ= {??,??}组成的字符串,即含有x个a,y个b的字符串
L={?, a, b, aa, ab, ba, bb, aaa, aab, aba, abb, baa, bab, bba, bbb} ,其中?表示空字符串,其它字符串均以上文提及的顺序排列
给定一个字母Σ= {??,??},列出L中所有长度小于5的字符串,其中L是所有以b开头并以b结尾的字符串。一些有效的单词是:bb,bab,bbb,baab,..
FSM的所有可接受的字符串应按字典顺序排序!
【JFLAP】
JFLAP是允许我们对FSM的操作进行建模的工具。
可以从这里下载JFLAP: http://www.cs.duke.edu/csed/jflap/
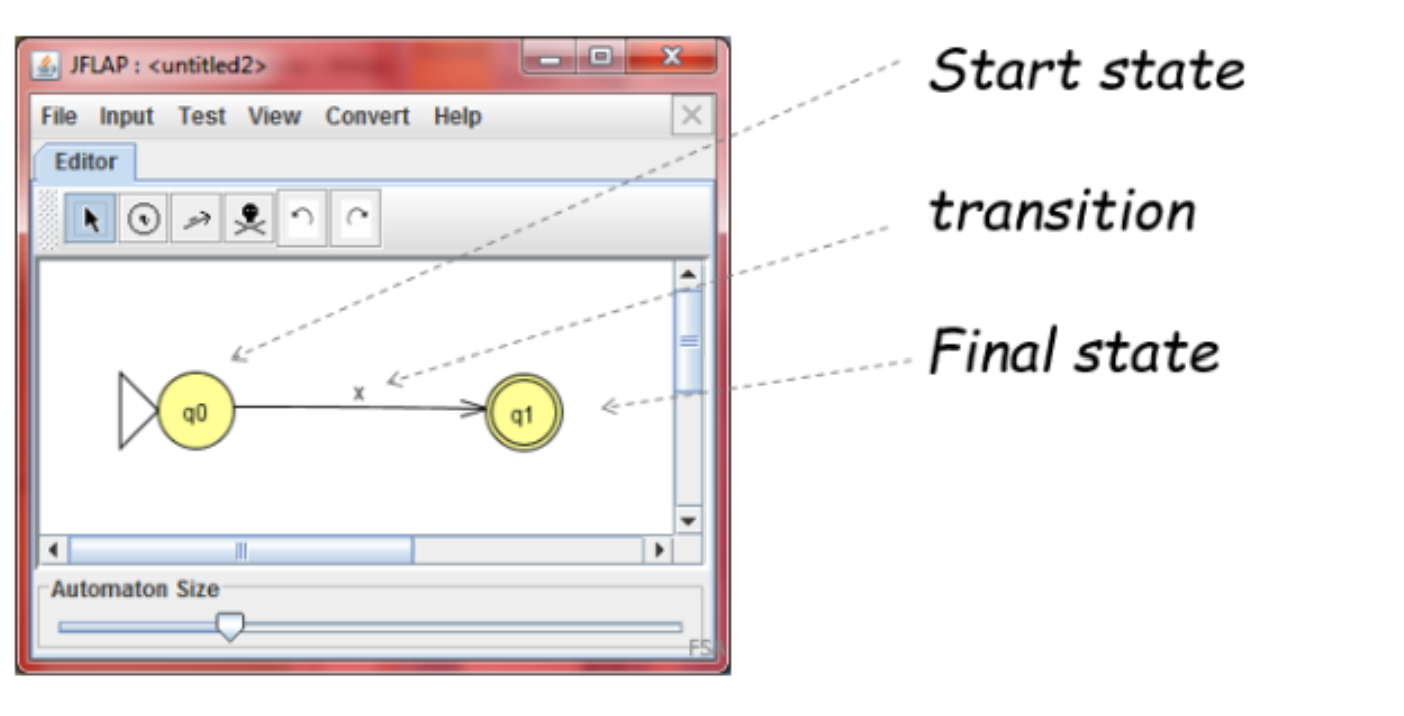
这个例子中,只有两个状态。从初始状态q0输入x就会转换为最终状态q1
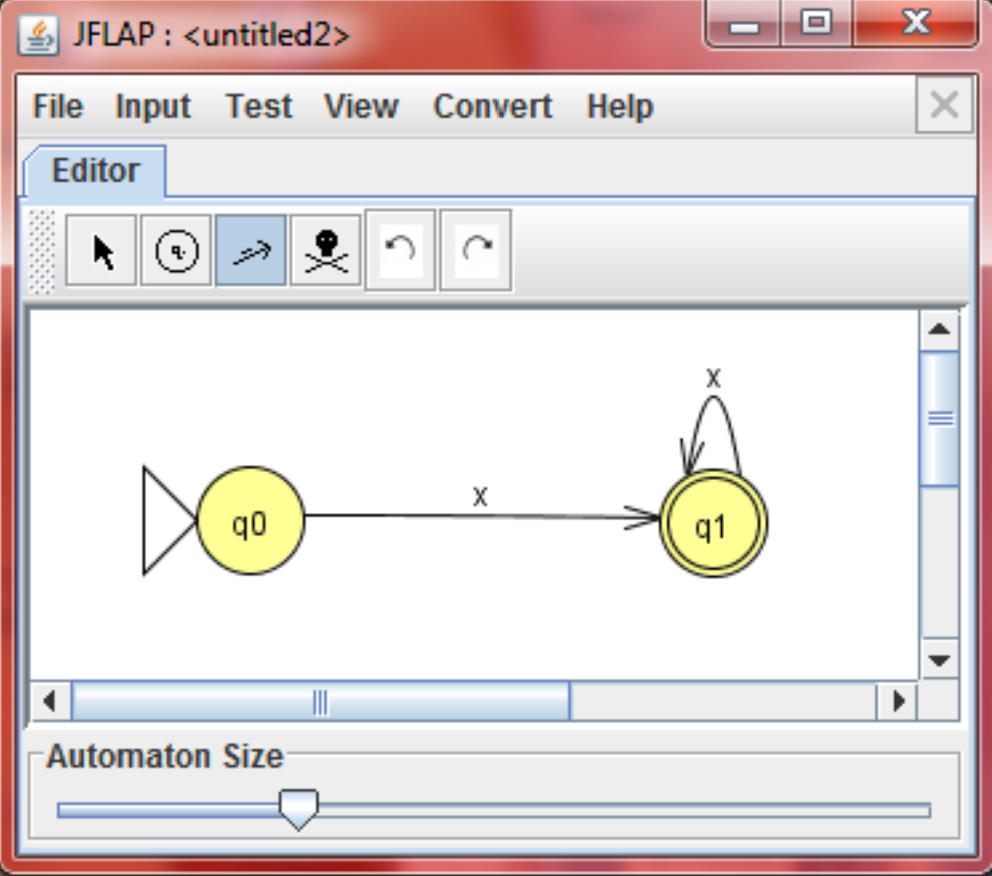
这个例子中,我们从初始状态q0输入x达到状态q1,之后持续输入x将在q1中循环接收
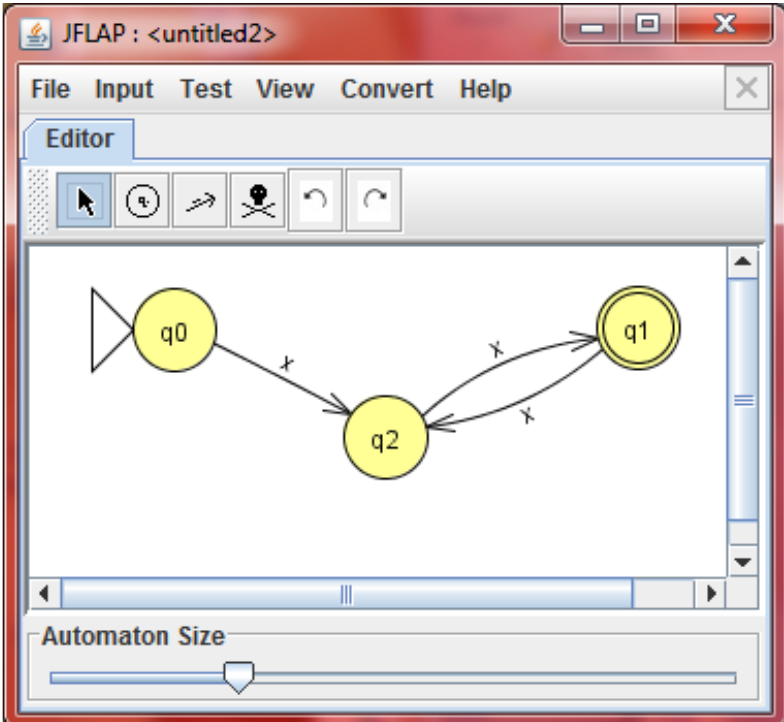
这个例子中,我们从初始状态q0输入x达到状态q2,之后持续输入x将在q1和q2中循环接收。这种情况下它只能接受偶数个个数的字符串
此时,因为q1q2的存在,q1接收x到q2,而q2再次接受x才会转化到q1(q1是最终状态),因此接收的x一定是偶数个
分析FSM后,您应该会看到仅接受x的偶数。我们从状态q0开始,并在得到x的输入时转换到状态q2。如果我们得到另一个x,我们将转换为状态q1。 q1是接受状态–当前单词在该语言中是否是有效单词?是的-因为该单词由两个x组成,即xx。如果再得到一个x或另外两个x或更多x,会发生什么情况? q1是接受状态,只有x的个数为偶数才能达到。
【确定性有限状态自动机(DFA) Deterministic Finite State Automata(DFA)】
确定性有限自动机(DFA)是一种FSM,在状态下每个标签仅具有一个过渡
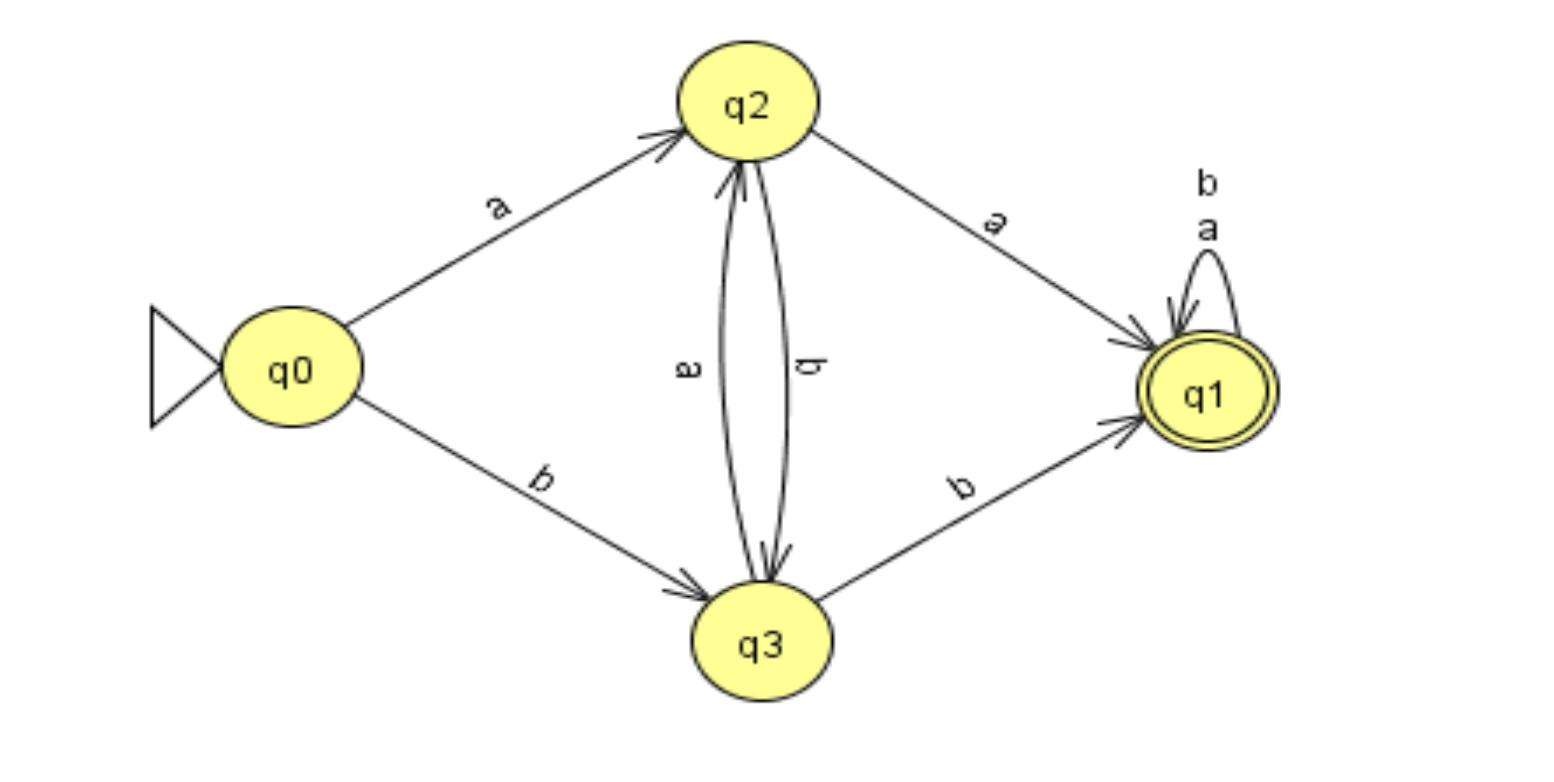
请注意,每个状态只有一个字母符号用于作离开状态的一个过渡
当我们处于某个状态时,一个符号对应一个下状态(每种状态接收到字母之后,下一个状态是确定性。不会出现在q1输入x,可能去q2,也可能q3的情况)
上图用表表示即:
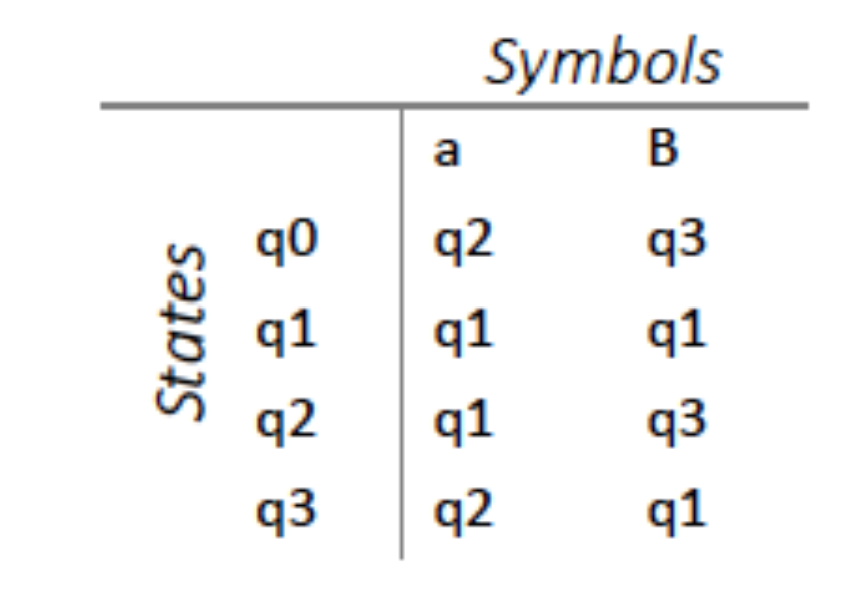
【非确定性有限自动机 Non-deterministic Finite Automata 】
了解了DFA之后,就可以用一张图来解释这种状态机了
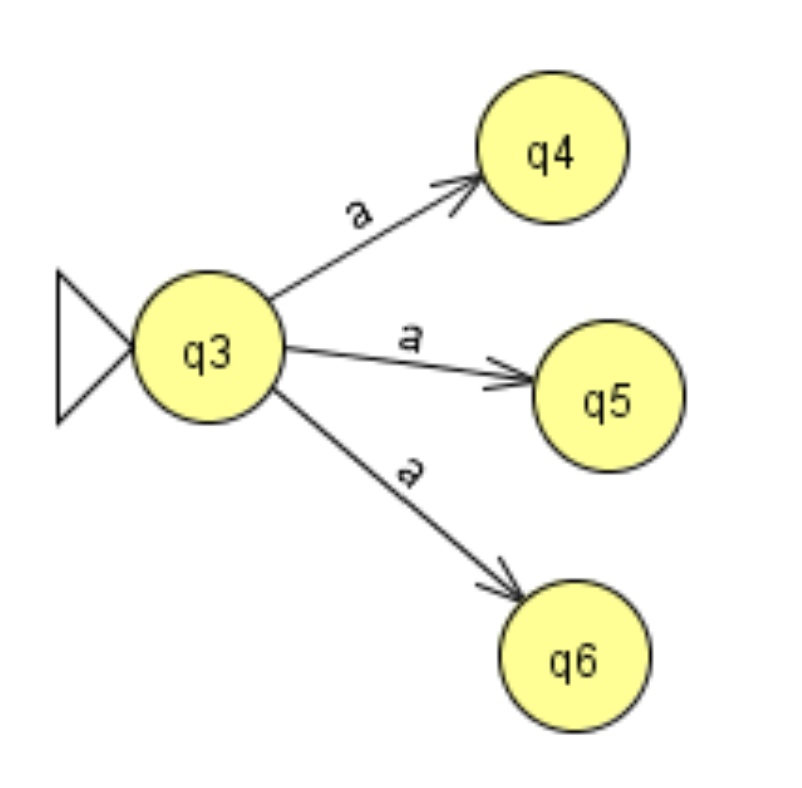
非确定性有限自动机(NFA)允许在多个状态下使用相同字母进行多次转换,这对应于状态转换表中单元中的两个(或多个)条目,它不是确定性的,因为下一个状态可以是许多可能状态中的任何一个。
【NFA和DFA的关系】
也就是说,对于任何NFA,我们都可以构建等效的DFA,反之亦然
虽然DFA和NFA有不同的定义,但可以证明它们是等同的。我们甚至可以在它们之间进行转换,但不是直接转化。
NFA和DFA都只承认正则语言
【练习和判断】
确定语言的方法是:
1.从开始状态开始,并按照图表进行操作,直到达到接受状态(一般就是最终状态)
2.以字典顺序列出在此状态下接受的字符串
【有限状态机的优势 Advantages of Finite State Machine】
1.灵活 Finite state machines are flexible
2.可以更简单的把抽象的工作,转化为具体代码的执行 Easy to move from a significant abstract to a code execution
3.处理器开销低 Low processor overhead
4.轻松确定状态的可达性 Easy determination of reachability of a state
【有限状态机的缺点 Disadvantages of Finite State Machine】
1.确定性不一定会被需要 The expected character of deterministic finite state machines can be not needed in some areas like computer games
2.如果没有任何设计思路,使用FSM实施大型系统很难进行管理,难以维护 The implementation of huge systems using FSM is hard for managing without any idea of design
3.不适用于所有领域 Not applicable for all domains
4.状态转换的顺序是不灵活的 The orders of state conversions are inflexible.
标签:computer eric not 报告 下载 eal versions execution 计算机
原文地址:https://www.cnblogs.com/RetenQ/p/14682928.html