标签:lazy can xixi 也有 为什么 保存 数据结构 量化 选择
前几天写了一篇canny边缘检测算法,比较偏算法公式和实现,具体为什么这样做和原理没有讲清楚,想在这一篇中讲一下,让研究canny算法的人不仅知道算法公式和实现,同时也能明白为什么这样做。
主要参考下面一个博客文章
https://www.cnblogs.com/xiximayou/p/13139426.html
这篇链接中,对于canny中每一步实现的目的给出了详细说明,比较通俗易懂。比如讲非极大值抑制,目的就是判断是否为局部最大值,如果不是,就可以排除不能够构成边缘的所有不需要的像素。目的,你得到的结果是带有“细边”的二进制图像,并给出了图示解释怎么获取到细边j。对于磁滞阈值法,同样给出图片讲解,目的是保存连接强边界的弱边界点,去除不连接强边界的弱边界点,同样也给出图片解释,比较容易通俗易懂。
1、非极大值抑制的目的:
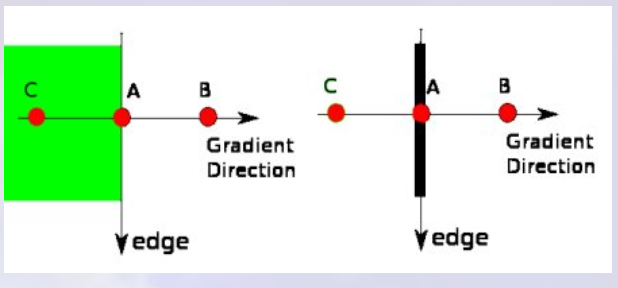
在获得梯度大小和方向后,将对图像进行全面扫描,以去除可能不构成边缘的所有不需要的像素。为此,在每个像素处,检查像素是否是其在梯度方向上附近的局部最大值。查看下面的图片:
2、磁滞阈值法
该阶段确定哪些边缘全部是真正的边缘,哪些不是。为此,我们需要两个阈值minVal和maxVal。强度梯度大于maxVal的任何边缘必定是边缘,而小于minVal的那些边缘必定是非边缘,因此将其丢弃。介于这两个阈值之间的对象根据其连通性被分类为边缘或非边缘。如果将它们连接到“边缘”像素,则将它们视为边缘的一部分。否则,它们也将被丢弃,见下图:
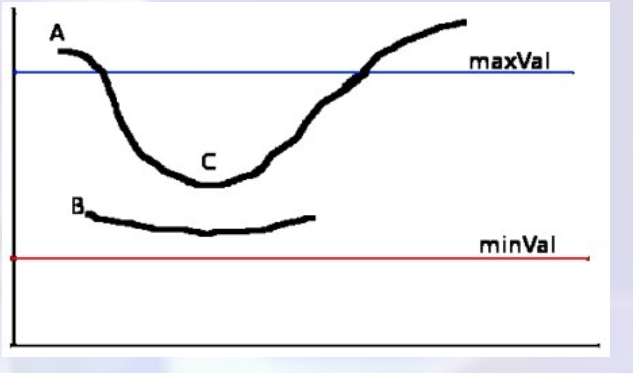
边缘A在maxVal之上,因此被视为“确定边缘”。尽管边C低于maxVal,但它连接到边A,因此也被视为有效边,我们得到了完整的曲线。但是边缘B尽管在minVal之上并且与边缘C处于同一区域,但是它没有连接到任何“确保边缘”,因此被丢弃。因此,非常重要的一点是我们必须相应地选择minVal和maxVal以获得正确的结果。
3、图片举例
3.1、非极大值抑制之前的边界信息图:

3..2、非极大值抑制处理,并且大于high阈值的强边界的图片:

3.3 基于非极大值抑制后的强边界基础上,进行磁滞阈值处理结果:
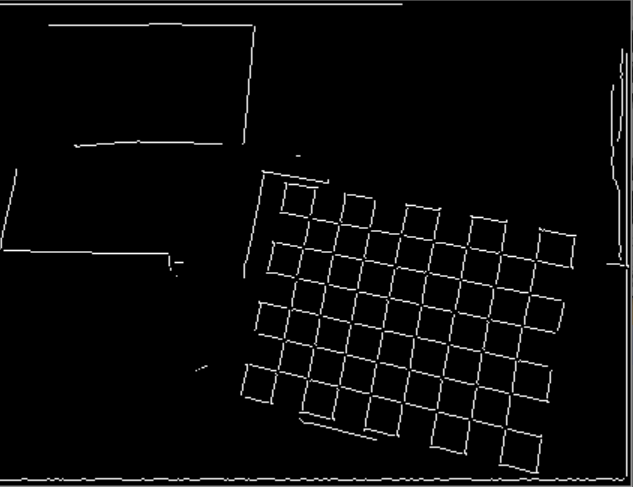
从上面三个图片可以看出确实将边界细化,同时凸显出强边界,最后一张加上部分弱边界点,将断断续续强边界连接起来了。广大网友如果看懂了canny算法的原理,就可以看上一篇的算法公式和边界方向量化手段,可以进行程序撰写。如果需要相关这方面的程序,可以给我发消息,我也可以提供。有opencv的mat数据结构实现的canny算法,也有直接用二维数组实现的canny算法。还有直接调用opencv的canny函数。
标签:lazy can xixi 也有 为什么 保存 数据结构 量化 选择
原文地址:https://www.cnblogs.com/happyhorse72/p/14756009.html