标签：load   word   问题   sha   搜索   function   html   统计   rgb   

一、K-近邻算法介绍

1.1定义

K Nearest Neighbor算法又叫KNN算法，定义为：如果一个样本在特征空间中的K个最相似（即特征空间中最近邻）的样本中的大多数属于某一个类别，则该样本也属于这个类别。定义不是太好理解，可以参考下图，假设你刚到北京，你下火车后你不知道你在那个区，但是你知道你4个朋友的位置和与你的距离，你就可以认为离你最近的朋友所在的区就是你所在的区。

在上面的例子中，衡量你与朋友之间的远近是依靠距离完成的，知道你的坐标位置和朋友的坐标位置通过欧式距离可以得出你们的相对位置。

下面讲个具体的案例，如下图，我们已经知道了一些电影的分类和一些基本特征（搞笑镜头、拥抱镜头、打斗镜头），然后知道一个新电影的特征，想知道它的分类便可以利用KNN计算。如下所示：

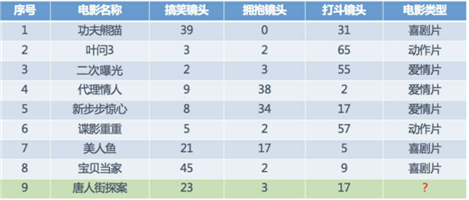
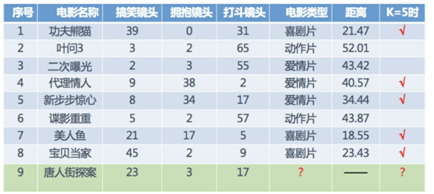
 从图上可以看出，在最近距离的五个电影中有三个喜剧片两个爱情片，故我们可认为唐人街探案为喜剧片（当然，结果可能不是太准确，有的人还说这是恐怖片呢）

注：衡量远近不一定非得欧式距离，还有曼哈顿距离,切比雪夫距离，闵可夫斯基距离等

1.2、KNN算法流程总结

1、计算已知类别数据集中的点与当前点之间的距离

2、按距离递增次序排序

3、选取与当前点距离最小的K个点

4、统计前K个点所在的类别出现的频率

5、返回前K个点出现频率最高的类别作为当前点的预测分类

二、K近邻算法的python中sklearn实现

KNeighborsClassifier( n_neighbors=5, *, weights=‘uniform‘, algorithm=‘auto‘, leaf_size=30, p=2, metric=‘minkowski‘, metric_params=None, n_jobs=None, **kwargs,)

参数     

　　　n_neighbors: int, 可选参数(默认为 5)

                用于[kneighbors](http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html#sklearn.neighbors.KNeighborsClassifier.kneighbors)查询的默认邻居的数量

        weights（权重）: str or callable(自定义类型), 可选参数(默认为 ‘uniform’)

                用于预测的权重函数。可选参数如下:

                       - ‘uniform’ : 统一的权重. 在每一个邻居区域里的点的权重都是一样的。

                       - ‘distance’ : 权重点等于他们距离的倒数。使用此函数，更近的邻居对于所预测的点的影响更大。

                       - [callable] : 一个用户自定义的方法，此方法接收一个距离的数组，然后返回一个相同形状并且包含权重的数组。

        algorithm（算法）: {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, 可选参数（默认为 ‘auto‘）

                计算最近邻居用的算法：

                       - ‘ball_tree’ 使用算法[BallTree](http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.BallTree.html#sklearn.neighbors.BallTree)

                       - ‘kd_tree’ 使用算法[KDTree](http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KDTree.html#sklearn.neighbors.KDTree)

                       - ‘brute’ 使用暴力搜索.

                       - ‘auto’ 会基于传入[fit](http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html#sklearn.neighbors.KNeighborsClassifier.fit)方法的内容，选择最合适的算法。

                注意 : 如果传入fit方法的输入是稀疏的，将会重载参数设置，直接使用暴力搜索。

         leaf_size（叶子数量）: int, 可选参数(默认为 30)

                传入BallTree或者KDTree算法的叶子数量。此参数会影响构建、查询BallTree或者KDTree的速度，以及存储BallTree或者KDTree所需要的内存大小。 此可选参数根据是否是问题所需选择性使用。

         p: integer, 可选参数(默认为 2)

                用于Minkowski metric（[闵可夫斯基空间](https://zh.wikipedia.org/wiki/%E9%96%94%E8%80%83%E6%96%AF%E5%9F%BA%E6%99%82%E7%A9%BA)）的超参数。p = 1, 相当于使用[曼哈顿距离](https://zh.wikipedia.org/wiki/%E6%9B%BC%E5%93%88%E9%A0%93%E8%B7%9D%E9%9B%A2) (l1)，p = 2, 相当于使用[欧几里得距离](https://zh.wikipedia.org/wiki/%E6%AC%A7%E5%87%A0%E9%87%8C%E5%BE%97%E8%B7%9D%E7%A6%BB)(l2)  对于任何 p ，使用的是[闵可夫斯基空间](https://zh.wikipedia.org/wiki/%E9%96%94%E8%80%83%E6%96%AF%E5%9F%BA%E6%99%82%E7%A9%BA)(l_p)

         metric（矩阵）: string or callable, 默认为 ‘minkowski’

                用于树的距离矩阵。默认为[闵可夫斯基空间](https://zh.wikipedia.org/wiki/%E9%96%94%E8%80%83%E6%96%AF%E5%9F%BA%E6%99%82%E7%A9%BA)，如果和p=2一块使用相当于使用标准欧几里得矩阵. 所有可用的矩阵列表请查询 DistanceMetric 的文档。

         metric_params（矩阵参数）: dict, 可选参数(默认为 None)

                给矩阵方法使用的其他的关键词参数。

         n_jobs: int, 可选参数(默认为 1)

                用于搜索邻居的，可并行运行的任务数量。如果为-1, 任务数量设置为CPU核的数量。不会影响[fit](http://scikit-learn.org/stable/modules/generated/sklearn.neighbors.KNeighborsClassifier.html#sklearn.neighbors.KNeighborsClassifier.fit)方法。

K-近邻算法

标签：load   word   问题   sha   搜索   function   html   统计   rgb   

原文地址：https://www.cnblogs.com/woyaofei/p/14756577.html