【工程应用四】 基于形状的多目标多角度的高速模板匹配算法进一步研究。

标签：公众号   memset   采样   str   工作   选择   布局   会同   mamicode   

      前面有两篇文章谈到了模板匹配算法，分别是【工程应用一】 多目标多角度的快速模板匹配算法（基于NCC，效果无限接近Halcon中........) 以及【工程应用二】 多目标多角度的快速模板匹配算法（基于边缘梯度)，那么经过最近2个多月的进一步研究，也有了更多的一些心得和体会，这里也简单分享一些在这个过程中属于我个人的理解的一些东西。

      1、在上一篇基于边缘梯度的文章中，我曾说使用Canny算子不合适，会丢失一些弱边缘的信息，但是后续我感觉还是可以的。

      2、在使用Canny后，一个很好的好处就是可以不做全图的计算了，这对速度的提高还是有很大的贡献的，通常Canny检测到的边缘占全图的像素数不会超出1/10,。

                扩展一下：  如果不做 Canny，而是对全图进行边缘检测后，按照边缘点的强度进行排序，然后取强度的前1/10作为候选点，也不失为一种解决问题的方法，但是测试发现偶尔会有丢失或误选目标的现象。

     3、对于旋转后的边缘问题，这个可以通过如下的方式进行解决。

               旋转后的无效的像素处，按照水平或者垂直方向的信息，对无效的区域的像素用离其水平或垂直方向最近的有效像素填充。选择水平方向实现最为简单和高效。

               一个简单的代码如下所示：

int IM_CorrectRotatedImage_Hori(HBitmap Src, HBitmap Mask)
{
    StartEnd *Hori = (StartEnd *)malloc(Mask.Height * sizeof(StartEnd));
    if (Hori == NULL)    return IM_STATUS_NULLREFRENCE;
    IM_SimpleMaskRLE_Hori(Mask, Hori);                            //    获取缩小后的水平行程
    for (int Y = 0; Y < Src.Height; Y++)
    {
        if (Hori[Y].Start != -1)
        {
            memset(Src.Data + Y * Src.Stride, Src.Data[Y * Src.Stride + Hori[Y].Start], Hori[Y].Start);
            memset(Src.Data + Y * Src.Stride + Hori[Y].End + 1, Src.Data[Y * Src.Stride + Hori[Y].End], Src.Width - Hori[Y].End - 1);
        }
    }
    int Top = -1, Bottom = -1;
    for (int Y = 0; Y < Src.Height; Y++)
    {
        if (Hori[Y].Start != -1)
        {
            Top = Y - 1;
            break;
        }
    }
    for (int Y = Src.Height - 1; Y >= 0; Y--)
    {
        if (Hori[Y].Start != -1)
        {
            Bottom = Y + 1;
            break;
        }
    }
    if (Top != -1)
    {
        for (int Y = 0; Y <= Top; Y++)
        {
            memcpy(Src.Data + Y * Src.Stride, Src.Data + (Top + 1) * Src.Stride, Src.Stride);
        }
    }

    if (Bottom != -1)
    {
        for (int Y = Src.Height - 1; Y >= Bottom; Y--)
        {
            memcpy(Src.Data + Y * Src.Stride, Src.Data + (Bottom - 1) * Src.Stride, Src.Stride);
        }
    }
    free(Hori);
    return IM_STATUS_OK;
}

        此时，再对此图做Canny边缘检测，则无效处因为填充的基本为同一像素或者近似，无效处的Canny值基本为0，在旋转的边缘处因为也是近似，值也约为0，即使不为0，也没有关系，旋转后的蒙版图也会把这些位置给裁剪掉，因此，不会产生新的边缘问题。如下所示：

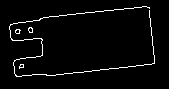
                    模板图                                    旋转一定角度的模板图             水平方向边缘填充                        Canny边缘检测                        旋转后对应的蒙版图                   根据蒙版裁切后的边缘图

         对于第一个模板，因为其边缘你基本为纯色，因此扩展后的图没有什么问题，而第二个图，扩展后的图进行检测，会看到在无效区域有一些额外的边缘出现，但是经过蒙版裁剪这些区域就消失了。

         4、对于得分公式，用 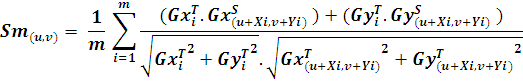  是完全可以的，注意的事情就是，对于模板图像 ，因为提取的候选点是用Canny选出来的，估计GX和GY一般也不会为0，至少不会同是为0，因此整个式子分母中的前半部分不会为0， 那么在编程时如果遇到在原图中的GX和Gy同时为0时，需要注意做特别处理，防止发生除以0的错误，即此位置的贡献为0（分子必然为0）。

         扩展：  整个表达式是一个归一化的式子，因为模板进行了Canny筛选，但是原图对应的位置是动态的，如果在原图中遇到那种比较光滑的地方（梯度值很小），比如GxS = 1， GyS = 2，这样的值，无论模板对应处的梯度如何，得分都会比较高，比如GxT = 230, GyT = 100，则此时此点的匹配度为：  1*230+2*100 /(sqrt(1*1+2*2)*sqrt(230*230+100*100)) =0.76， 很明显，我们觉得这样的情况是不可以接受的，因此，个人觉得对于这样的点，应该在计算分值时予以剔除（不急于得分加成中）。

      5、为了减少Canny检测的噪音，可在检测前进行适当的模糊，高斯模糊、均值模糊、保边模糊随你选，但是半径不易过大，而且要注意随着金字塔的下采样，因为下采样本身就是一种平均，因此模糊的半径应该怎么样来着？？？？？？

      6、CodeProject上印度小哥的得分贪心算法可以应用上，这个对于金字塔顶层的速度提高有较为明显的作用，但是对于后续的向上扩展搜索加速作用有限，这个主要是因为后续的候选点得分本身就比较高了，那个贪心的要求标准也越来越难以达到。

      7、算法的速度优化上有很多方法，1个是原理上的，一个是编码上的。

          （1）原理上的，前面说的金字塔时根本，Canny检测减少候选点是主攻，贪心算法是甜点。另外就是在各层的新的候选点的筛选上，也应该逐层减少，操作的原则可以是： 两个候选点的坐标位置过进，取得分大的。 候选点之间的区域重叠度过大， 可以只取得分高者等等。

           （2）编码上则八仙过海，各显神通了，我最擅长的是SIMD指令优化。这里提几个小的Trick。

            a、梯度值的保存。  上述边缘的梯度值Gx和Gy根据数据的范围，很明显最合适使用的数据类型是signed short。

            b、在SIMD指令中有一个_mm_madd_epi16，其函数原型为：

                       extern __m128i _mm_madd_epi16(__m128i _A, __m128i _B);

                   我在我博客里多次提前这个函数，他可以一次性型实现8个short类型数据的乘法和4次int类型的加法，如下所示：  

                    如果我们布局的时候，把梯度的X和Y方向数据连续布置，那么得分公式的分子和分母的四个部分乘法和加法（下面的平方也是乘法）就可以直接利用这样的指令实现了，具体的自己好好理解吧。

            c、求根号是个比较慢的计算过程，SIMD指令有_mm_sqrt_ps指令一次性实现4个浮点数的开方，那么按照上面的式子就还需要求倒数，我们首先把得分式子的分母中的两个根号里的数据相乘，然后在开方，结果是一样的，很明显就少了一次开方操作，         同时，注意到SIMD里还有一个指令，即_mm_rsqrt_ps，他可以一次性的完成开方和求倒数工作，因此速度就更快了。

           d、另外还有一个点，我们在向金字塔底层搜索的过程中，一般的搜索半径为2，即搜索区域为5*5大小，对于这个尺寸，还可以一次性处理4个点，这样就组成 6*4+1个组合，这种组合比直接计算单独的25个点要速度快很多，因为他避免了对模板数据的多次重复读取和计算。

           8、除了速度，还有算法稳定性问题，这个也是个比较难的问题，我目前也还遇到一些情况，比如不同的起点角度，都是慢360度的搜索方位，返回的角度值可能有轻微的波动，还比如有些情况可能会丢失一些目标或找到了多余的目标等等。这个还需要后续继续研究，比较增加过程中的亚像素参与等。

           9、比较了下halcon的create_shape_model和find_shape_model，发现他的模型文件都特别特别的小，只有几十KB，而且create_shape_model的过程基本是几豪秒杀，因此，感觉他的结构应该更为敲门，也许是用到了亚像素方面的特性，需要慢慢看有么有机遇找到这方面的资料了。

           10、halcon有基于形状的多目标、多角度、多缩放尺度的模板检测，这个现在也在想，如何减少计算量，有点麻烦。

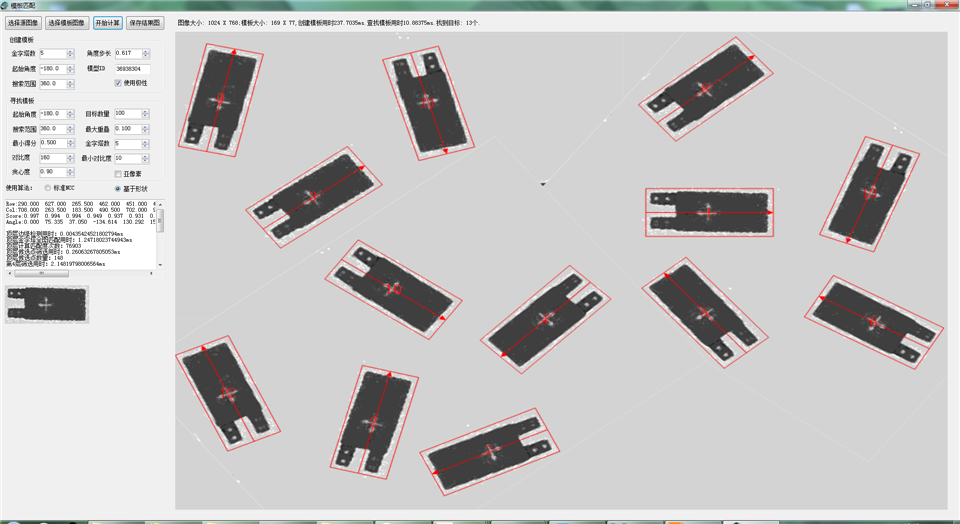
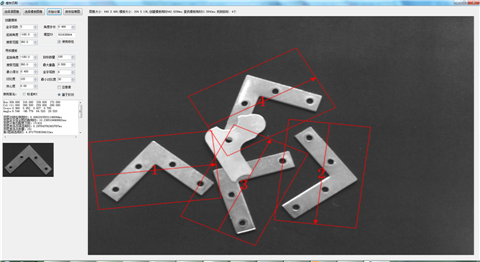
           目前，经过一番骚操作，基于形状的匹配在速度上有的时候居然比基于NCC的还快了不少，而且结果上也比较稳定。

           如果哪位在工程实践中有需要类似的功能，我可以提供函数接口和Demo（基于边缘的算法），不过唯一的要求就是提供一些实际的素材供我测试算法用。

           这里提供一个例子供大家测试： https://files.cnblogs.com/files/Imageshop/TemplateMatching.rar

           如果想时刻关注本人的最新文章，也可关注公众号：     

【工程应用四】 基于形状的多目标多角度的高速模板匹配算法进一步研究。

标签：公众号   memset   采样   str   工作   选择   布局   会同   mamicode   

原文地址：https://www.cnblogs.com/Imageshop/p/14821562.html