标签:技术 倍增 没有 ble load 并且 进入 等于 图片
https://www.luogu.com.cn/problem/P7599
考虑找到 \((B,C)\) 区间内的最高树 \(M\) 和 \([C,D]\) 中的最高树 \(N\)
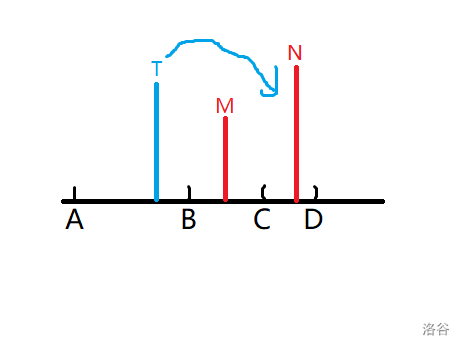
那么最后一步跳跃一定是从某棵满足 {\(H_M \le H_T \le H_N\)} 且 {\((T,M)\) 中没有比 \(T\) 更高的树} 的树 \(T\) 跳进 \([C,D]\) 区间中
我们把所有这样的树 \(T\) 叫做"准终点"
所以原问题的目标就等价于用最少的步数跳到一个准终点上 然后再跳一步进入 \([C,D]\)
如果 \([A,B]\) 中存在一个准终点,那么显然可以直接从那棵树出发,只需一步即可完成
否则,最优方案应该从 \([A,B]\) 中满足 {\((P,M)\) 中没有比 \(P\) 更高的树} 的树中最高的那棵 \(P\) 开始 下面给出证明
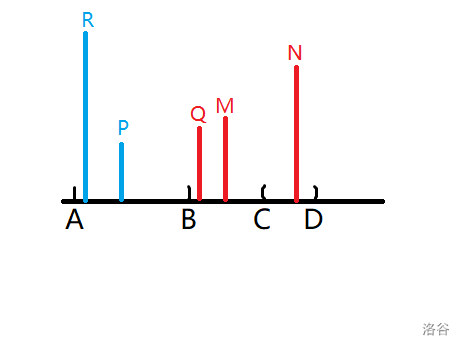
如图,\(R\) 是 \(P\) 向左跳一次到的那棵树,\(Q\) 是向右跳一次到的那棵树
由于上文假设 \([A,B]\) 中没有合法的准终点 ,所以树 \(R\) 比 树 \(N\) 更高,所以向右跳一次一定会到达 \(D\) 右边,因此 \([A,R]\) 区间的树都不能作为起点
对于 \((R,P)\) 区间的树,它们的高度全部小于 \(H[P]\)。如果想要跳出 \((R,P)\) 区间,不论怎么跳都会到达 \(R,P\) 其中一棵树,一定没有从 \(P\) 开始优
对于 \((P,Q)\) 区间的树同理,一定会跳到 \(P,Q\) 其中一棵树,然而 \(P\) 只需一步就能跳到 \(Q\) ,所以一定没有 \(P\) 优秀
所以从 \(P\) 出发一定最优,QED
从第 \(B\) 棵树开始,倍增地向左跳,跳到最左边的一棵在 \(A\) 之前并且高度小于树 \(N\) 的树,它就是最优出发点
如果它是准终点,那么只需一步,否则需要多步
对于一棵树,可以向左跳或者向右跳,我们把跳到左右中较高的一棵树称作跳高边,反之叫跳低边
有如下跳的策略:
容易发现这就是最优策略
实现时先从最优出发点出发,倍增跳高边跳到最高的一棵高度小于树 \(M\) 的为止 假设是树 \(X\)
检查从 \(X\) 跳高边到的那棵树是不是准终点
如果不是,那就从 \(X\) 出发倍增向右跳跳到最高的一棵高度小于树 \(M\) 的为止,然后检查它向右跳一步是不是准终点
所有的步骤都可以使用ST表或者倍增实现,所以总时间复杂度是 \(O((n+q)\log n)\)
标签:技术 倍增 没有 ble load 并且 进入 等于 图片
原文地址:https://www.cnblogs.com/ak-dream/p/14825110.html