标签:数值 线性 选择排序 遇到 基数排序 array nlog 映射关系 java
分类
外排序:由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行(k路归并)
内排序:所有操作再内存就可以完成
比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
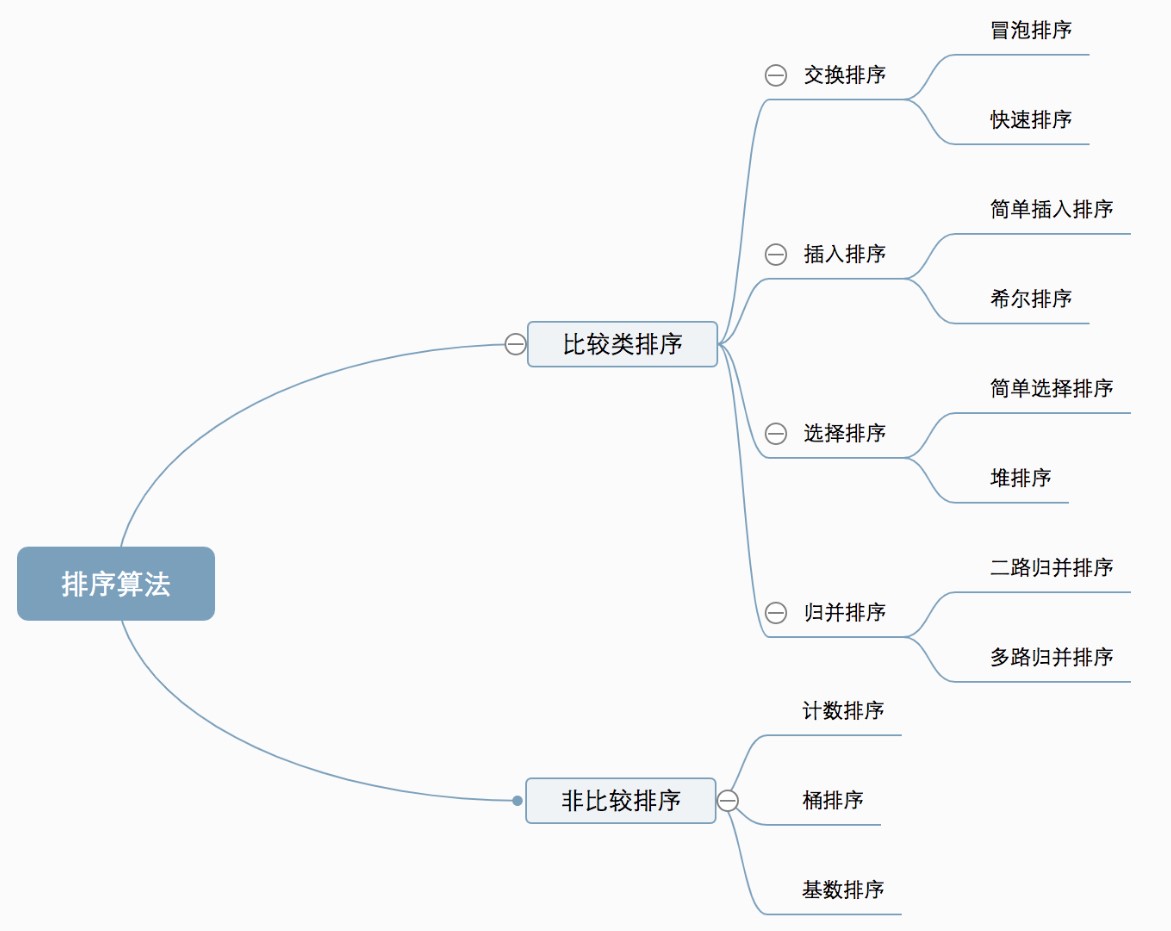
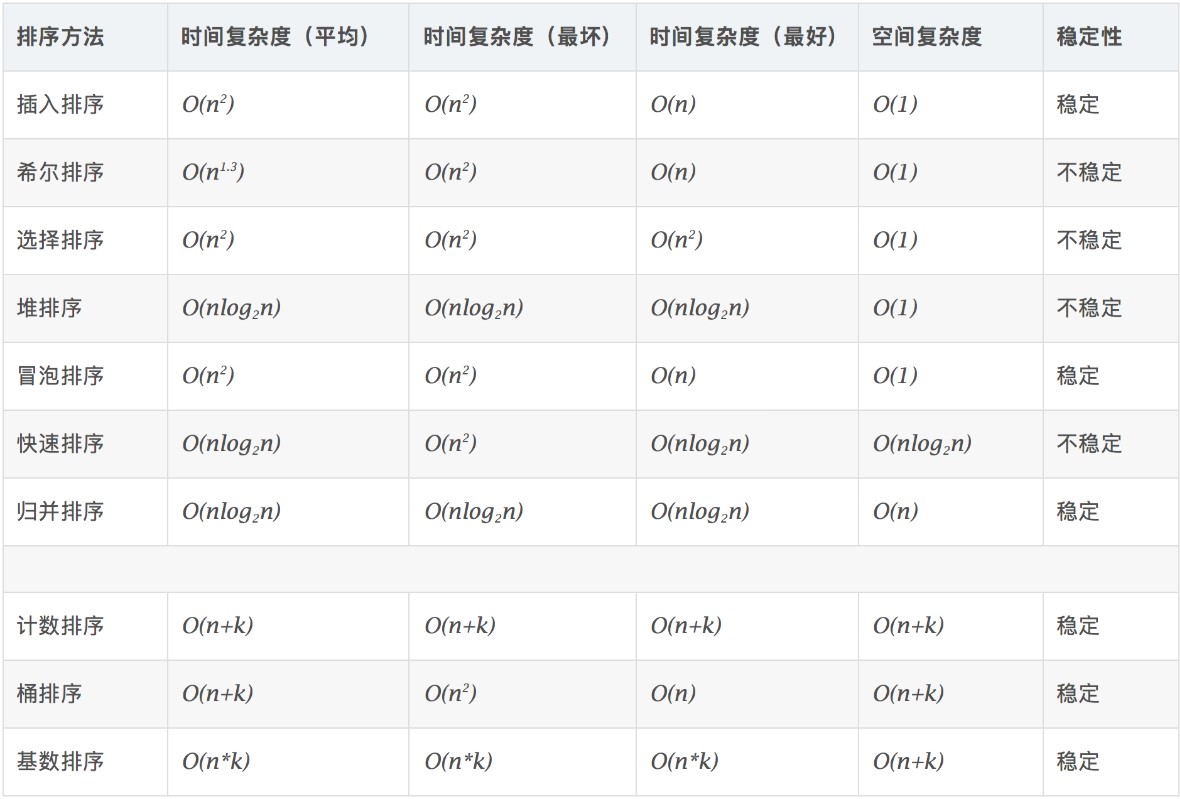
冒泡排序:
比较两个相邻的元素,如果前一个比后一个大,就交换 = 每次回确定一个最大数并且交换到对应的末位
public static void main(String[] args) {
int[] arr = {2, 4, 1, 14, 22, -5, 9, 0};
int len = arr.length;
for (int i = 0; i < len; i++) {
for (int j = 1; j < len - i; j++) {
//前一个比后面的大就交换
if (arr[j - 1] > arr[j]) {
int tmp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = tmp;
}
}
}
System.out.println(Arrays.toString(arr));
}
选择排序:
初始状态:无序区为 [0, n),有序区为空
每次从无序区找到第i小的数,将其与i位置的数交换,无序区减一
public static void main(String[] args) {
int[] arr = {2, 4, 1, 14, 22, -5, 9, 0};
int len = arr.length;
for (int i = 0; i < len - 1; ++i) {
int min = i;
for (int j = i + 1; j < len; ++j) {
if (arr[min] > arr[j]) {
min = j;
}
}
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
System.out.println(Arrays.toString(arr));
}
插入排序:
初始状态:一般认为第数组的一个数是已排序状态,之后为还未排序区域
每次将当前数与前一个数比较,如果比前一个数小,就交换,直到遇到比它小的或到头了
public static void main(String[] args) {
int[] arr = {2, 4, 1, 14, 22, -5, 9, 0};
for (int i = 1; i < arr.length; i++) {
int inNext = arr[i]; //待排序的数
int index = i - 1; //待排序数的前一个数下标
while (index >= 0 && inNext < arr[index]) {
arr[index + 1] = arr[index];
index--;
} //退出循环代表以找到位置
arr[index + 1] = inNext;
}
System.out.println(Arrays.toString(arr));
}
希尔排序:(缩小增量排序)
简单插入排序的改进版,与插入排序的不同之处在于,它会优先比较距离较远的元素
思路:每次对数组分为Len/2组,每组进行比较交换,每次分组越来越细
public static void main(String[] args) {
int[] arr = {2, 4, 1, 14, 22, -5, 9, 0};
// sort(arr);
sortMove(arr);
}
//交换法
public static void sort(int[] arr) {
int temp = 0;
for (int interval = arr.length / 2; interval > 0; interval /= 2) {
for (int i = interval; i < arr.length; i++) {
for (int j = i - interval; j >= 0; j -= interval) {
if (arr[j] > arr[j + interval]) {
temp = arr[j];
arr[j] = arr[j + interval];
arr[j + interval] = temp;
}
}
}
}
System.out.println(Arrays.toString(arr));
}
//移位法
public static void sortMove(int[] arr) {
for (int interval = arr.length / 2; interval > 0; interval /= 2) {
for (int i = interval; i < arr.length; i++) {
int j = i;
int temp = arr[j];
if (arr[j] < arr[j - interval]) {
while (j - interval >= 0 && temp < arr[j - interval]) {
arr[j] = arr[j - interval];
j -= interval;
}
arr[j] = temp;
}
}
}
System.out.println(Arrays.toString(arr));
}
归并排序:
该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并
步骤:分 -> 合
把长度为n的输入序列分成两个长度为n/2的子序列;
对这两个子序列分别采用归并排序;
将两个排序好的子序列合并成一个最终的排序序列;
//分 : 将数组按二分法分为左右子数组(左右指针),递归,直到left == right跳出递归;
//合 : 设置两个指针分别对应左右数组,比较大小按序合并为一个数组
快速排序:
快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。(分治法)
步骤
从数列中挑出一个元素,称为 “基准”(pivot);
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
public static void main(String[] args) {
int[] arr ={32,6,88,63,2,95,33,8};
sort(arr);
System.out.println(Arrays.toString(arr));
}
?
public static void sort(int[] arr){
int first = 0;
int tail = arr.length-1;
sort(arr,first,tail);
}
?
public static void sort(int[] arr,int first,int tail){
if (first<tail){
int index = partition(arr,first,tail);
//向左排序
sort(arr,first,index-1);
//向右排序
sort(arr,index+1,tail);
}
}
?
public static int partition(int[] arr, int first, int tail){
int i = first;
int j = tail;
int temp = arr[first];
while (i<j){
//从右到左,找到第一个小于temp的值
while (arr[j]>=temp && i<j){
j--;
}
//将找到的值填入arr[i],i指针向右移一位
if (i<j){
arr[i] = arr[j];
i++;
}
//从左到右,找到第一个大于temp的值
while (arr[i]<temp && i<j){
i++;
}
//将找到的值填入arr[j],j指针向左移一位
if (i<j){
arr[j] = arr[i];
j--;
}
}
arr[i] = temp;
return i;
}
优化:
对于快排,最主要的点就是基准值的确定,当基准值的数值在中间区域时是最优的,当基准值是最大或者最小时,快排的时间复杂度将是最差的[O(n^2)]
可以对区间取左,右,中三个数,取中位数为基准值
堆排序:
堆排序(HeapSort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点
Java中优先队列(PriorityQueue)实现的方式
步骤:
计数排序
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数
桶排序
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序
基数排序
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前
步骤:
取得数组中的最大数,并取得位数;
arr为原始数组,从最低位开始取每个位组成bucket数组;
对bucket进行计数排序(利用计数排序适用于小范围数的特点);
public static void main(String[] args) {
int[] arr ={44,256,77,2,89,60,456};
sort(arr);
System.out.println(Arrays.toString(arr));
}
?
public static void sort(int[] arr){
int[][] bucket = new int[10][arr.length];
int[] Effectiveindex = new int[10];
//找出数组最大的数,得出最大数的位数,来确定循环次数
int max = arr[0];
for (int i=1;i<arr.length;i++){
if (arr[i]>max){
max = arr[i];
}
}
int max_length = (max +" ").length();//计算max的位数
for (int k=0,n=1;k<max_length;k++,n *=10){
//按基数放数据;记录存放次数
for (int i=0;i<arr.length;i++){
int Remainder = arr[i] /n % 10;
bucket[Remainder][Effectiveindex[Remainder]] = arr[i];
Effectiveindex[Remainder]++;
}
int index = 0;
//将桶里的数依次放入原数组
for (int j=0;j<Effectiveindex.length;j++){
if (Effectiveindex[j]!=0){//存放进j桶的次数
for (int p=0;p<Effectiveindex[j];p++){
arr[index++] = bucket[j][p];
}
}
Effectiveindex[j]=0;
}
}
}
标签:数值 线性 选择排序 遇到 基数排序 array nlog 映射关系 java
原文地址:https://www.cnblogs.com/hehell/p/14860760.html