标签:each 定义 bsp blank 进制转化 注意 超过 退出 radix
二分法练习
一、PAT甲级1010

题目描述:给出两个不超过10位的“数字”,给出其中一个数的基数(表示这个数是几进制),现在给出的两个数在各自的进制下是相等的,要求找出另一个数在什么进制下与已给出的数相等,如果不存在就返回impossible
输入中:N1,N2表示输入的两个数;radix表示其中一个数的基数,tag1表示radix是N1的基数,tag2同理
二、问题分析
按照题目的描述最高是z表示35,所以这些数最大是36进制,如果对已经给出基数的数分别求各个进制下的表示,这样太复杂,很有可能超时。
按照二分的思想,可以把这个算法想象成一个猜数字游戏,于是这个算法就变成从数组2~36中找一个数作为符合要求的基数,可以用二分查找法,为了方便计算就把两个数都转成10进制进行比较。
三、算法描述
分析:首先要分析二分查找的过程,不妨假设一下,已知十进制数120,现在找78对应的基数,使得78=120(78这个数是我用120在16进制转化而来,所以要求的目标结果就是16);那么先取(2+36)/2=19作为基数,计算8*19^0+7*19^1=133;因为133比120大,而且预期结果是16,所以可以断定19取大了,那么就向下压缩,这样就可以得到核心算法了
核心算法:定义三个变量l,r,mid分别作为下界,上界,结果。int l=2,r=36,mid;
循环条件为l<r while(l<r)
每次循环计算mid=(r+l)/2;
以mid为基数计算对应10进制数,如果结果比N1(假设给出的tag=1)的十进制形式大,就取r=mid-1;小就取l=mid+1,等就退出循环取mid为基数
如果循环结束时l=r就输出impossiblle
优化:这里因为n2这个数是给出的,只要找出n2中每位数字里的最大值,这个最大值可以作为下界,而不需要以2为下界
下面定义数据结构;首先需要一个数据结构来对应a-z的值,可以使用一个结构体,手动打表,但是C++中数组下标可以使用字母(https://blog.csdn.net/alovelypeach/article/details/114271843)所以直接用字母当下标就行
四、代码



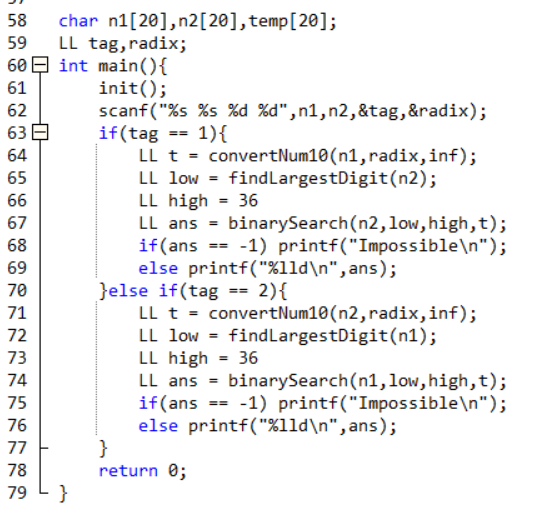
注意,该代码无法在PAT运行,可以在devc++中运行,应该是编译器的问题,这里的代码只是一种思路,可以有多种不同的代码样式,但核心思想就是上述提出的
标签:each 定义 bsp blank 进制转化 注意 超过 退出 radix
原文地址:https://www.cnblogs.com/zyq79434/p/14872787.html