标签:style blog http io color ar os sp strong
前面的文章介绍过二分查找、散列表查找;二分查找效率为Θ(lgn)、二分查找要求数组是静态的,即元素不能动态的插入和删除,否则会耗费较多的时间;散列表查找效率可以到达Θ(1),但是一般用于“等于性查找“,不能进行“范围查找”;本文介绍的二叉查找树,(1)能实现动态查找,查找效率仍能达到Θ(lgn);(2)也能方便的进行范围查找;
除了上面的查找,二叉查找树还能实现动态的插入和删除操作。并且期望效率能达到Θ(lgn)
Question 1、那么,什么是二叉查找树呢?
二叉查找树,也叫二叉搜索树、二叉排序树。是一种特殊的二叉树,数据结构可以用二叉链表结构表示;二叉查找树关键字满足如下特性:设x为二叉查找树中的一个结点。如果y是x的左子树中的一个结点,则key[y]≤key[x]。如果y是x的右子树中的一个结点,则key[x]≤key[y]
二叉查找树有一个很好的特性:中序遍历二叉查找树能输出一组有序的节点序列;其中,中序遍历运行时间为Θ(n)。
Question 2、二叉排序树各种操作的效率如何?
二叉树可以实现的操作包括:基本查询,查询最小、最大关键值、前驱、后继,单个节点的插入和删除操作。这些操作的效率与二叉树的高度成正比,一颗随机构造的二叉查找树的期望高度为O(lgn),从而基本动态集合的操作平均时间为Θ(lgn),注意这里只是期望效率,最坏情况下为Θ(n),在二叉查找树存在的问题小节中会进行讲解原因及如何改进使其最坏情况下达到Θ(lgn)
节点中包括关键字元素key,卫星数据,每个节点还包含属性left,right和parent,他们指向节点的左孩子、右孩子、和双亲。
1 //二叉查找树节点定义,带模板 2 template <class T> 3 class BinarySearchTreeNode 4 { 5 public: 6 T key;//节点值,这里只有一个关键元素值,没有附带数据(卫星数据) 7 BinarySearchTreeNode<T>* parent;//指向双亲节点指针 8 BinarySearchTreeNode<T>* left;//指向左孩子节点指针 9 BinarySearchTreeNode<T>* right;//指向右孩子节点指针 10 };
二叉查找树中最常见的操作是查找树中的某个关键字,除了基本的查询,还支持最大值、最小值、前驱和后继查询操作
2.2.1、基本查询
这个过程从树根开始查找,并沿着这棵树中一条简单路径向下进行,对遇到的每个节点x,比较关键字k(待查找的关键字)与x.key。如果两个关键字相等,查找就终止。如果k小于x.key,查找在x的左子树中继续。对称地,如果k大于x.key,查找在右子树中继续。重复此过程,知道找到或者遇到空节点为止。下图是查找元素4的流程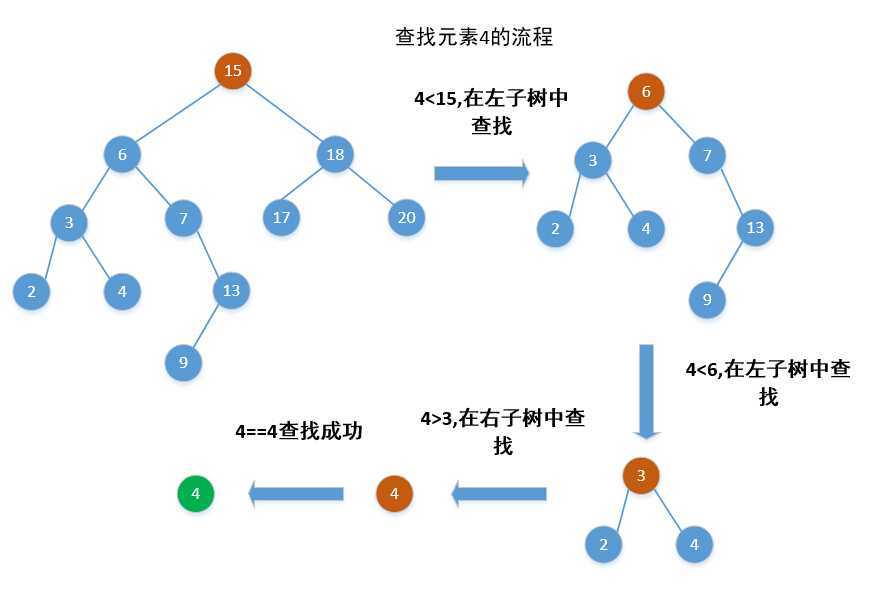
查找过程伪码:
递归:
1 TREE_SEARCH(x,k) 2 if x=NULL or k=key[x] 3 then return x 4 if(k<key[x]) 5 then return TREE_SEARCH(left[x],k) 6 else 7 then return TREE_SEARCH(right[x],k)
非递归:
1 ITERATIVE_TREE_SEARCH(x,k) 2 while x!=NULL and k!=key[x] 3 do if k<key[x] 4 then x=left[x] 5 else 6 then x=right[x] 7 return x
2.2.1、查询最小、最大关键字
根据二叉查找树的特征,很容易查找出最大和最小关键字。查找二叉树中的最小关键字:从根结点开始,沿着各个节点的left指针查找下去,直到遇到NULL时结束。如果一个结点x无左子树,则以x为根的子树中,最小关键字就是key[x]。查找二叉树中的最大关键字:从根结点开始,沿着各个结点的right指针查找下去,直到遇到NULL时结束。查找最大最小关键字的伪代码:
最小关键字
1 TREE-MINIMUM(x) 2 while x.left != NIL 3 x = x.left 4 return x
最大关键字
1 TREE_MAXIMUM(x) 2 while x.right != NIL 3 do x= x.right 4 return x
2.2.1、查询前驱和后继
给定一个二叉查找树中的结点,找出在中序遍历顺序下某个节点的前驱和后继。如果树中所有关键字都不相同,则某一结点x的前驱就是小于key[x]的所有关键字中最大的那个结点,后继即是大于key[x]中的所有关键字中最小的那个结点。根据二叉查找树的结构和性质,不用对关键字做任何比较,就可以找到某个结点的前驱和后继。
查找前驱步骤:先判断x是否有左子树,如果有则在left[x]中查找关键字最大的结点,即是x的前驱。如果没有左子树,则从x继续向上执行此操作,直到遇到某个结点是其父节点的右孩子结点。则该父亲节点即为前驱节点。例如下图查找结点7的前驱结点6过程: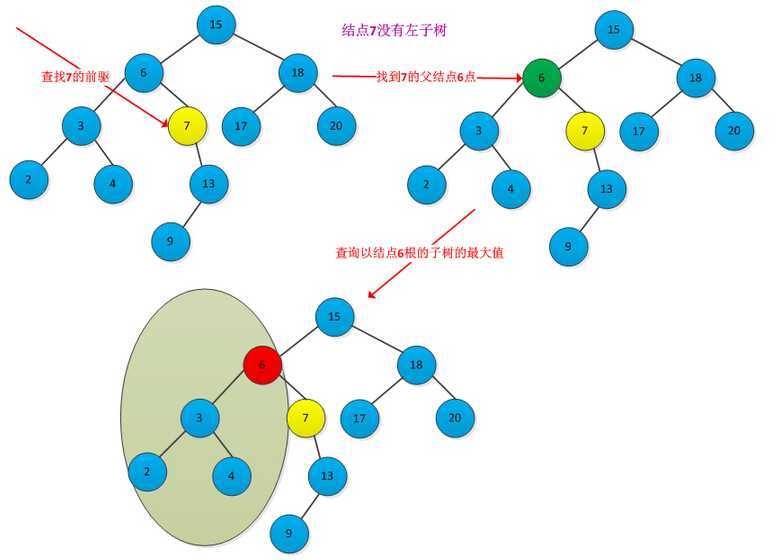
查找后继步骤:先判断x是否有右子树,如果有则在right[x]中查找关键字最小的结点,即使x的后继。如果没有右子树,则从x的父节点开始向上查找,直到遇到某个结点是其父结点的左儿子的结点时为止,则该父亲节点即为后继节点。例如下图查找结点13的后继结点15的过程:
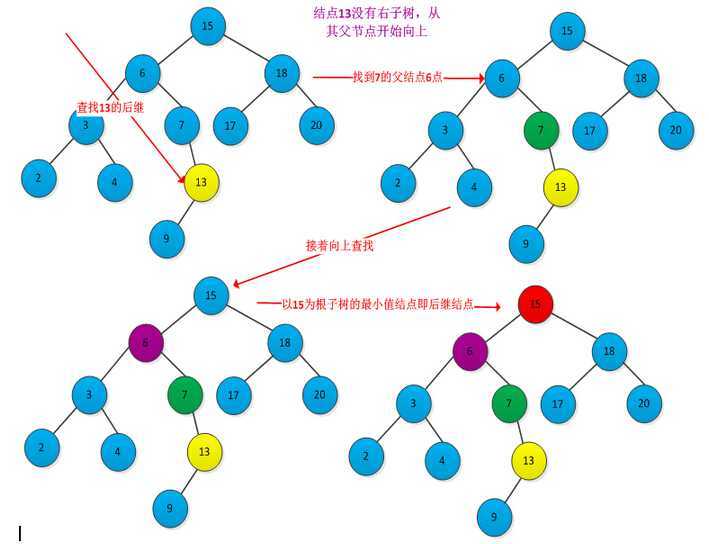
求x前驱节点的伪码:
1 TREE_PREDECESSOR(x) 2 if left[x] != NULL 3 then return TREE_MAXIMUM(left(x)) 4 y=parent[x] 5 while y!= NULL and x ==left[y] 6 do x = y 7 y=parent[y] 8 return y
求x后继节点的伪码:
1 TREE_SUCCESSOR(x) 2 if right[x] != NULL 3 then return TREE_MINMUM(right(x)) 4 y=parent[x] 5 while y!= NULL and x ==right[y] 6 do x = y 7 y=parent[y] 8 return y
插入结点的位置对应着查找过程中查找不成功时候的结点位置,因此需要从根结点开始查找带插入结点位置,找到位置后插入即可。下图所示插入结点过程: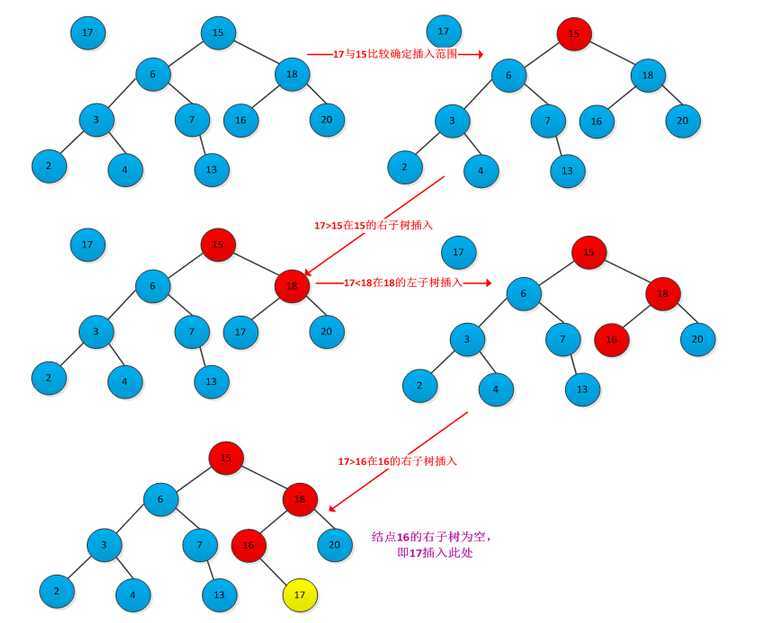
插入过程伪代码:
1 TREE_INSERT(T,z) 2 y = NULL; 3 x =root[T] 4 while x != NULL 5 do y =x 6 if key[z] < key[x] 7 then x=left[x] 8 else x=right[x] 9 parent[z] =y 10 if y=NULL 11 then root[T] =z 12 else if key[z]>key[y] 13 then keft[y] = z 14 else right[y] =z
删除操作比较复杂,从二叉查找树中删除给定的节点z,分三种情况:
<1>结点z没有左右子树,则修改其父节点p[z],使其为NULL。
<2>如果结点z只有一个子树(左子树或者右子树),那么将这个孩子提升到树中z的位置上,并修改z的父节点,用z的孩子来替换z.
<3>如果z有两个子女,则先删除z的后继y(y没有左孩子),在用y的内容来替代z的内容。
下面的分析把上述情况分成4种情况进行详细讲解:
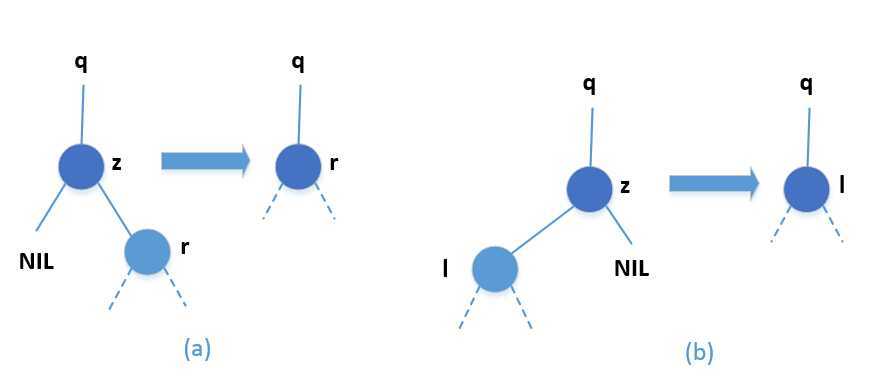
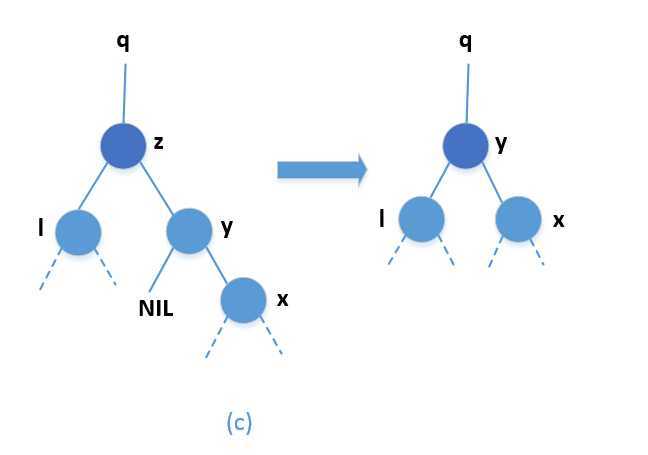
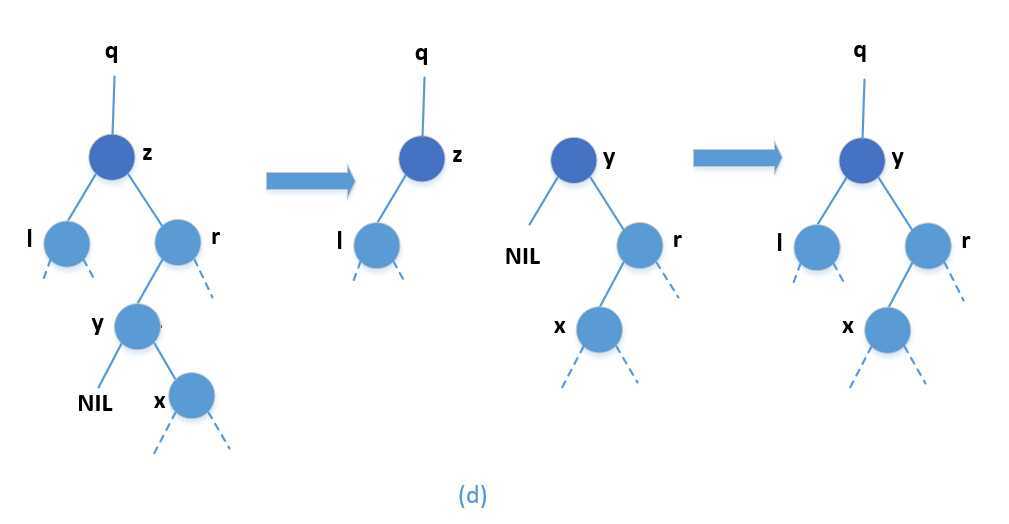
在写删除伪代码之前,为了在二叉查找树内移动子树,先定义一个子过程TRANSPLANT,它是用另一颗子树替换一颗子树并成为其双亲的孩子节点。当TRANSPLANT用一颗以v为根的子树来替换一颗以u为根的子树是,节点u的双亲就变为节点v的双亲,并且最后v成为u的双亲的相应孩子。
TRANSPLANT子过程伪代码:
1 TRANSPLANT(T,u,v) 2 if u.p == NIL 3 T.root = v 4 elseif u == u.p.left//如果u是一个左孩子 5 u.p.left = v 6 else u.p.right = v//如果u是一个右孩子 7 if v != NIL 8 v.p = u.p
利用现成的TRANSPLANT过程,下面是二叉搜索树T中删除节点z的删除过程:
1 TREE-DELETE(T,z) 2 if z.left == NIL //图a,左孩子为空,用z的右孩子替换掉z 3 TRANSPLANT(T,z,z.right) 4 elseif z.right == NIL////图b,右孩子为空,用z的左孩子替换掉z 5 TRANSPLANT(T,z,z.left) 6 else //左右孩子都存在 7 y = TREE-SUCCESSOR(z)//z的后继 8 if y.p != z//y不是z的右孩子 9 TRANSPLANT(T,y,y.right)//y的右孩子替换掉y 10 y.right = z.right//z的右孩子转换为y的右孩子 11 y.right.p = y 12 TRANSPLANT(T,z,y)//用y替换z并成为z的双亲的一个孩子 13 y.left = z.left//再用z的左孩子替换为y的左孩子 14 y.left.p = y
二叉查找上各种基本操作的运行时间都是O(h),h为树的高度。但是在元素插入和删除过程中,树的高度会发生改变。如果n个元素按照严格增长的顺序插入,那个构造出的二叉查找树的高度为n-1。例如按照先后顺序插入7、15、18、20、34、46、59元素构造二叉查找树,二叉查找树结构如下所示:
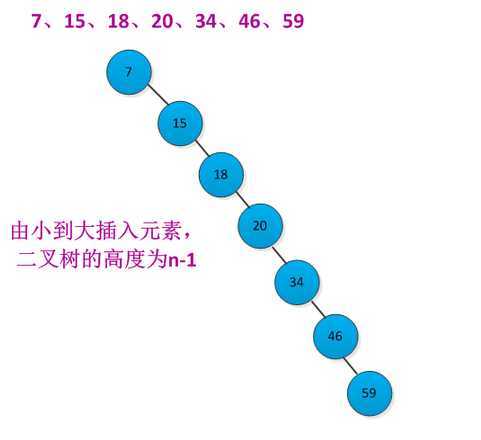
这样就导致二叉查找树的基本操作运行时间是Θ(n),解决方法就是"旋转"二叉树,使二叉树"平衡",比如平衡二叉树、红黑树等。这些在其他文章里面讲解。
BinarySearchTree.h(二叉查找树实现)

1 #include <iostream> 2 #include <stack> 3 using namespace std; 4 5 //二叉查找树节点定义,带模板 6 template <class T> 7 class BinarySearchTreeNode 8 { 9 public: 10 T key;//节点值,这里只有一个值,没有附带数据 11 BinarySearchTreeNode<T>* parent;//指向双亲节点指针 12 BinarySearchTreeNode<T>* left;//指向左孩子节点指针 13 BinarySearchTreeNode<T>* right;//指向右孩子节点指针 14 }; 15 16 /* 17 二查查找树功能实现类,包括节点查找,最大、最小节点查找, 18 前驱、后继节点查找,插入节点,删除节点功能实现,带模板 19 */ 20 template <class T> 21 class BinarySearchTree 22 { 23 public: 24 BinarySearchTree(); 25 void tree_insert(const T& elem); 26 int tree_remove(const T& elem); 27 BinarySearchTreeNode<T>* tree_search(const T& elem)const; 28 BinarySearchTreeNode<T>* tree_minmum(BinarySearchTreeNode<T>* root)const; 29 BinarySearchTreeNode<T>* tree_maxmum(BinarySearchTreeNode<T>* root)const; 30 BinarySearchTreeNode<T>* tree_successor(const T& elem) const; 31 BinarySearchTreeNode<T>* tree_predecessor(const T& elem)const; 32 bool empty() const; 33 void inorder_tree_traverse()const; 34 BinarySearchTreeNode<T>* get_root()const { return root; } 35 void transplant(BinarySearchTreeNode<T>* u, BinarySearchTreeNode<T>* v); 36 private: 37 BinarySearchTreeNode<T>* root; 38 }; 39 /*构造函数*/ 40 template <class T> 41 BinarySearchTree<T>::BinarySearchTree() 42 { 43 root = NULL; 44 } 45 /*二叉查找树插入操作实现 46 实现思路:插入结点的位置对应着查找过程中查找不成功时候的结点位置, 47 因此需要从根结点开始查找带插入结点位置,找到位置后插入即可 48 */ 49 template <class T> 50 void BinarySearchTree<T>::tree_insert(const T& elem) 51 { 52 if (!empty())//判断二叉树是否为空,非空则找到合适节点插入 53 { 54 BinarySearchTreeNode<T> *pnode = root; 55 BinarySearchTreeNode<T> *qnode = NULL; 56 BinarySearchTreeNode<T> *newnode = new BinarySearchTreeNode<T>;//创建新节点 57 newnode->key = elem;//插入节点值 58 newnode->parent = NULL;//初始化双亲节点、左右孩子节点 59 newnode->left = NULL; 60 newnode->right = NULL; 61 while (pnode)//非空,查找插入节点位置 62 { 63 qnode = pnode; 64 if (pnode->key > elem)//当前节点值大于待插入节点值,向左子树查找 65 pnode = pnode->left; 66 else//当前节点值不大于待插入节点值,向右子树查找 67 pnode = pnode->right; 68 } 69 if (qnode->key > elem)//当前节点值大于待插入节点值,则插入到左孩子节点 70 qnode->left = newnode; 71 else//否则插入到右孩子节点 72 qnode->right = newnode; 73 newnode->parent = qnode;//设置新插入节点的双亲节点 74 } 75 else//二叉树为空,则插入节点为根节点 76 { 77 root = new BinarySearchTreeNode<T>; 78 root->key = elem; 79 root->parent = NULL; 80 root->left = NULL; 81 root->right = NULL; 82 } 83 } 84 /*删除节点调用的子过程transplant,用一颗子树v替换另外一颗子树u并成为其双亲的孩子节点 85 输入:u-被替换的子树指针,v-新替换的子树指针 86 输出:void 87 */ 88 template <class T> 89 void BinarySearchTree<T>::transplant(BinarySearchTreeNode<T>* u, BinarySearchTreeNode<T>* v) 90 { 91 if (u->parent == NULL) root = v; 92 else if (u == u->parent->left) u->parent->left=v; 93 else u->parent->right = v; 94 95 if (v != NULL) v->parent = u->parent; 96 } 97 /*节点删除实现 98 输入:要删除的节点的关键字 99 输出:删除成功返回0 100 不存在此关键字则返回-1 101 */ 102 template <class T> 103 int BinarySearchTree<T>::tree_remove(const T&elem) 104 { 105 BinarySearchTreeNode<T> *pnode;//当前节点 106 BinarySearchTreeNode<T> *snode;//双亲节点、后继节点 107 pnode = tree_search(elem);//查找待删除节点 108 if (!pnode) return -1;//待删除节点不存在,返回-1 109 if (pnode->left == NULL)//左孩子不存在,用右孩子直接替换待删除节点(这个右孩子可以是NULL,也可以不是NULL) 110 transplant(pnode, pnode->right); 111 else if (pnode->right == NULL)//只存在左孩子,用左孩子直接替换待删除节点 112 transplant(pnode,pnode->left); 113 else//左右孩子都存在 114 { 115 snode = tree_minmum(pnode->right);//求待删除节点的后继(因右孩子存在,所以一定是右子树中最小的节点) 116 if (snode->parent != pnode)//后继不是待删除节点的右孩子, 117 { 118 transplant(snode, snode->right);//snode是后继节点,所以无左子树,右子树替换掉snode 119 snode->right = pnode->right;//pnode的右孩子成为snode的右孩子 120 snode->right->parent = snode; 121 } 122 transplant(pnode, snode);//snode替换掉pnode 123 snode->left = pnode->left;//处理snode的左子树,及左子树的双亲关系 124 snode->left->parent = snode; 125 } 126 return 0; 127 128 } 129 /*查找search实现 130 输入:待查找的数据elem 131 输出:查找成功,返回指向该节点的指针; 132 待查找数值不存在,返回空指针 133 */ 134 template <class T> 135 BinarySearchTreeNode<T>* BinarySearchTree<T>::tree_search(const T& elem)const 136 { 137 BinarySearchTreeNode<T> *pnode = root;//节点指针,指向根节点 138 //非递归查找过程 139 while (pnode)//节点非空 140 { 141 if (pnode->key == elem)//查找成功:指针指向节点关键值等于待查找数值,退出while 142 break; 143 else if (pnode->key > elem)//当前节点值大于查找的elem,则在当前节点左孩子二叉树中进行查找 144 pnode = pnode->left; 145 else //当前节点值小于查找的elem,则在当前节点右孩子二叉树中进行查找 146 pnode = pnode->right; 147 } 148 149 return pnode; 150 } 151 152 /*查找最小关键字 153 输入:指向要查找的二叉树的根节点的指针 154 输出:返回指向最小关键字节点的指针 155 */ 156 template <class T> 157 BinarySearchTreeNode<T>* BinarySearchTree<T>::tree_minmum(BinarySearchTreeNode<T>* root)const 158 { 159 BinarySearchTreeNode<T> *pnode = root;//节点指针,指向根节点 160 161 while (pnode->left)//从根结点开始,沿着各个节点的left指针查找下去,直到遇到NULL时结束 162 pnode = pnode->left; 163 164 return pnode; 165 } 166 /*查找最d大关键字 167 输入:指向要查找的二叉树的根节点的指针 168 输出:返回指向最大关键字节点的指针 169 */ 170 template <class T> 171 BinarySearchTreeNode<T>* BinarySearchTree<T>::tree_maxmum(BinarySearchTreeNode<T>* root)const 172 { 173 BinarySearchTreeNode<T> *pnode = root;//节点指针,指向根节点 174 175 while (pnode->right)//从根结点开始,沿着各个节点的left指针查找下去,直到遇到NULL时结束 176 pnode = pnode->right; 177 178 return pnode; 179 } 180 /*求节点后继 181 输入:当前节点的值 182 输出: 当前节点的后继节点的指针 183 */ 184 template <class T> 185 BinarySearchTreeNode<T>* BinarySearchTree<T>::tree_successor(const T& elem) const 186 { 187 BinarySearchTreeNode<T>* pnode = tree_search(elem);//查找值为elem的节点,返回指针保存到pnode 188 BinarySearchTreeNode<T>* parentnode=NULL;//定义双亲节点 189 if (pnode != NULL)//当前节点存在 190 { 191 if (pnode->right)//当前节点存在右孩子,则后继为右子树的最小关键字节点 192 return tree_minmum(pnode->right); 193 parentnode = pnode->parent;//不存在右孩子,取双亲节点 194 /* 195 //双亲节点不为空,并且当前节点时双亲节点的右孩子时,一直寻找双亲节点, 196 //直到双亲节点为空,或者当前节点是双亲节点的左孩子 197 */ 198 while (parentnode && pnode == parentnode->right) 199 { 200 pnode = parentnode; 201 parentnode = parentnode->parent; 202 } 203 if (parentnode)//双亲节点不为空,返回 204 return parentnode; 205 else//为空,无后继节点 206 return NULL; 207 } 208 return NULL;//当前节点不存在 209 } 210 /*求节点前驱 211 输入:当前节点的值 212 输出: 当前节点的前驱节点的指针 213 */ 214 template <class T> 215 BinarySearchTreeNode<T>* BinarySearchTree<T>::tree_predecessor(const T& elem)const 216 { 217 BinarySearchTreeNode<T>* pnode = tree_search(elem);//查找值为elem的节点,返回指针保存到pnode 218 BinarySearchTreeNode<T>* parentnode;//定义双亲节点 219 if (pnode != NULL)//当前节点存在 220 { 221 if (pnode->right) 222 return tree_maxmum(pnode->right);//当前节点存在左孩子,则后继为左子树的最大关键字节点 223 parentnode = pnode->parent;//不存在左孩子,取双亲节点 224 /* 225 //双亲节点不为空,并且当前节点是双亲节点的左孩子时,一直寻找双亲节点, 226 //直到双亲节点为空,或者当前节点是双亲节点的右孩子 227 */ 228 while (parentnode && pnode == parentnode->left) 229 { 230 pnode = parentnode; 231 parentnode = pnode->parent; 232 } 233 if (parentnode)//双亲节点不为空,返回 234 return parentnode; 235 else//为空,无后继节点 236 return NULL; 237 } 238 return NULL; 239 } 240 /*判断二叉树查找树是否为空 241 输出:若为空,返回true 242 非空,返回false 243 */ 244 template <class T> 245 bool BinarySearchTree<T>::empty() const 246 { 247 return (NULL == root); 248 } 249 /*二叉查找树中序遍历非递归实现 250 实现思路:借助栈完成 251 */ 252 template <class T> 253 void BinarySearchTree<T>::inorder_tree_traverse()const 254 { 255 if (NULL != root) 256 { 257 stack<BinarySearchTreeNode<T>*> s; 258 BinarySearchTreeNode<T> *ptmpnode; 259 ptmpnode = root;//指向根节点 260 while (NULL != ptmpnode || !s.empty())//当前节点不空,或者栈不空 261 { 262 if (NULL != ptmpnode)//当前节点不为空,入栈,置左孩子节点为当前节点 263 { 264 s.push(ptmpnode);//入栈 265 ptmpnode = ptmpnode->left;//置左孩子节点为当前节点 266 } 267 else//当前节点为空,弹出栈顶元素并访问该节点,然后置右孩子节点为当前节点 268 { 269 ptmpnode = s.top();//弹出栈顶元素 270 s.pop(); 271 cout << ptmpnode->key << " ";//访问该节点 272 ptmpnode = ptmpnode->right; //然后置右孩子节点为当前节点 273 } 274 } 275 } 276 }
Main.cpp(主测试函数)

1 #include"BinarySearchTree.h" 2 int main() 3 { 4 BinarySearchTree<int> bstree; 5 BinarySearchTreeNode<int>* ptnode, *proot; 6 bstree.tree_insert(32); 7 bstree.tree_insert(21); 8 bstree.tree_insert(46); 9 bstree.tree_insert(54); 10 bstree.tree_insert(16); 11 bstree.tree_insert(38); 12 bstree.tree_insert(70); 13 cout << "inorder tree walk is: "; 14 bstree.inorder_tree_traverse(); 15 proot = bstree.get_root(); 16 cout << "\nmax value is: " << bstree.tree_maxmum(proot)->key << endl; 17 cout << "min value is: " << bstree.tree_minmum(proot)->key<< endl; 18 ptnode = bstree.tree_search(38); 19 if (ptnode) 20 cout << "the element 38 is exist in the binary tree.\n"; 21 else 22 cout << "the element 38 is not exist in the binary tree.\n"; 23 cout << "the successor of 38 is: " << bstree.tree_successor(38)->key << endl; 24 cout << "the predecessor of 38 is:" << bstree.tree_predecessor(38)->key << endl; 25 if (bstree.tree_remove(46) == 0) 26 cout << "delete 46 successfully" << endl; 27 else 28 cout << "delete 46 failed" << endl; 29 cout << "inorder tree walk is: "; 30 bstree.inorder_tree_traverse(); 31 exit(0); 32 }
运行结果: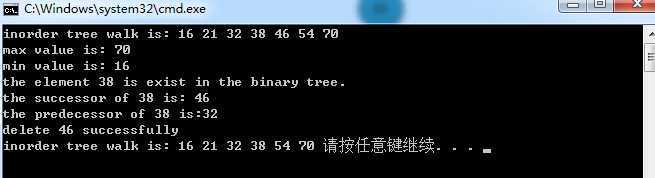
(个人想法):二叉排序树是否可以用来进行对数组进行排序呢?效率是多少?堆排序也是构造二叉树,他们的特点各是什么?(设平均高度为O(lgn))
答(如有不妥请大神指点):(1)可以排序,首先把每个节点插入到而叉查找树中构造完整二叉查找树,然后进行中序遍历即可得到有序序列;其中插入单个节点时间为Θ(lgn),n个节点用时Θ(nlgn),所以二叉排序树排序效率为Θ(nlgn)。
(2)堆排序是一颗完全二叉树,排序效率为Θ(nlgn),需要构造大顶堆或者小顶堆。边调整堆边交换元素排序。完成后进行层序遍历即可得到有序序列;
(3)二叉排序树可以不是完全二叉树,堆排序是一颗完全二叉树。
【1】 http://www.cnblogs.com/Anker/archive/2013/01/28/2880581.html
【2】http://www.cnblogs.com/huangxincheng/archive/2012/07/21/2602375.html
【3】《算法导论》
标签:style blog http io color ar os sp strong
原文地址:http://www.cnblogs.com/zhoutaotao/p/4096237.html