算法——权重最短路径算法

标签：oat   start   最短路径算法   __name__   com   site   join   process   ESS   

迪克斯特拉

最小权重路径

示例1

"""
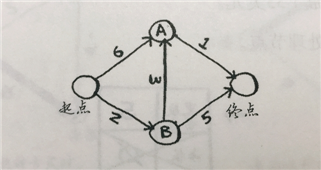
需要三个字段：流程图(各个节点)，权重图(启点到各个节点)，父节点(各个节点)，是否处理过的一个数组
"""

graph = {}
graph[‘start‘] = {}
graph[‘start‘][‘a‘] = 6
graph[‘start‘][‘b‘] = 2

graph[‘b‘] = {}
graph[‘b‘][‘a‘] = 3
graph[‘b‘][‘end‘] = 5

graph[‘a‘] = {}
graph[‘a‘][‘end‘] = 1

graph[‘end‘] = {}

infinity = float("inf")
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["end"] = infinity

parents = {}
parents[‘a‘] = "start"
parents[‘b‘] = "start"
parents[‘end‘] = None

processed = []

class DiKeSiTeLa():

    def find_lowest_cost_node(self, costs):
        """
        找到开销最小的节点
        """
        lowest_cost = float(‘inf‘)
        lowest_cost_node = None
        for node in costs:
            cost = costs[node]
            if cost < lowest_cost and node not in processed:
                lowest_cost_node = node
                lowest_cost = cost
        return lowest_cost_node


if __name__ == "__main__":
    di = DiKeSiTeLa()
    node = di.find_lowest_cost_node(costs)
    while node is not None:
        cost = costs[node]
        nighbors = graph[node]
        for n in nighbors.keys():
            new_cost = cost + nighbors[n]
            if costs[n] > new_cost:
                costs[n] = new_cost
                parents[n] = node
        processed.append(node)
        node = di.find_lowest_cost_node(costs)
    
    
    print(costs)
    print(parents)
    # {‘a‘: 5, ‘b‘: 2, ‘end‘: 6}
    # {‘a‘: ‘b‘, ‘b‘: ‘start‘, ‘end‘: ‘a‘}

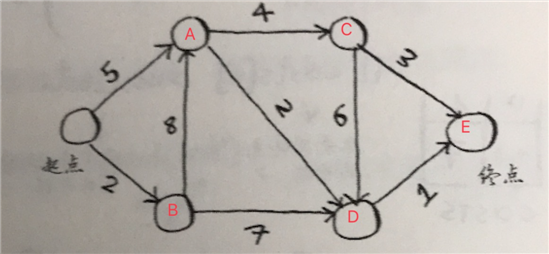
示例2

graph = {
    ‘start‘: {
        ‘a‘: 5,
        ‘b‘: 2
    },
    ‘a‘: {
        ‘c‘: 4,
        ‘d‘: 2
    },
    ‘b‘: {
        ‘a‘: 8,
        ‘d‘: 7
    },
    ‘c‘: {
        ‘end‘: 3,
        ‘d‘: 6
    },
    ‘d‘: {
        ‘end‘: 1
    },
    ‘end‘: {}
}
# 权重
inf = float(‘inf‘)
costs = {}
costs[‘a‘] = 5
costs[‘b‘] = 2
costs.update({
    ‘c‘: inf,
    ‘d‘: inf,
    ‘end‘: inf
})
# 父节点
parents = {
    ‘a‘: ‘start‘,
    ‘b‘: ‘start‘,
    ‘c‘: None,
    ‘d‘: None,
    ‘end‘: None
}
# 已处理的节点
processed = []

def find_lowest_cost_node(costs):
    lowest_node = None
    lowest_node_cost = float(‘inf‘)
    for node in costs:
        if costs[node] < lowest_node_cost and node not in processed:
            lowest_node_cost = costs[node]
            lowest_node = node
    return lowest_node

def shortest_way(parents):
    way = []
    next = ‘end‘
    while next != ‘start‘:
        way.append(next)
        next = parents.get(next)
    return ‘ --> ‘.join([‘start‘]+way[::-1])

if __name__ == ‘__main__‘:
    node = find_lowest_cost_node(costs)
    while node:
        nighbors = graph[node]
        for n in nighbors.keys():
            new_cost = costs[node] + nighbors[n]
            if costs[n] > new_cost:
                costs[n] = new_cost
                parents[n] = node
        processed.append(node)
        node = find_lowest_cost_node(costs)
    print(costs)  # {‘a‘: 5, ‘b‘: 2, ‘c‘: 9, ‘d‘: 7, ‘end‘: 8}
    print(parents)  # {‘a‘: ‘start‘, ‘b‘: ‘start‘, ‘c‘: ‘a‘, ‘d‘: ‘a‘, ‘end‘: ‘d‘}
    print(shortest_way(parents))  # start --> a --> d --> end

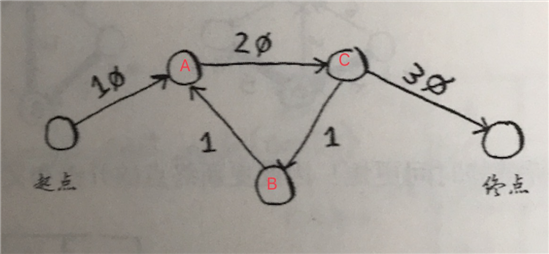
示例3

from 迪克斯特拉算法2_A import shortest_way

grahp = {
    ‘start‘: {
        ‘a‘: 10
    },
    ‘a‘: {
        ‘c‘: 20
    },
    ‘c‘: {
        ‘end‘: 30,
        ‘b‘: 1
    },
    ‘b‘: {
        ‘a‘: 1
    },
    ‘end‘: {}
}
inf = float(‘inf‘)
costs = {
    ‘a‘: 10,
    ‘b‘: inf,
    ‘c‘: inf,
    ‘end‘: inf
}
parents = {
    ‘a‘: ‘start‘,
    ‘b‘: ‘c‘,
    ‘c‘: ‘a‘,
    ‘end‘: ‘c‘
}
processed = []

def find_lowest_cost_node(costs):
    lowest_node = None
    lowest_node_cost = inf
    for node in costs:
        if lowest_node_cost > costs[node] and node not in processed:
            lowest_node = node
            lowest_node_cost = costs[node]
    return lowest_node

if __name__ == "__main__":
    node = find_lowest_cost_node(costs=costs)
    while node:
        highbors = grahp[node]
        for n in highbors.keys():
            new_cost = costs[node] + highbors[n]
            if costs[n] > new_cost:
                costs[n] = new_cost
                parents[n] = node
        processed.append(node)
        node = find_lowest_cost_node(costs=costs)
    print(costs)  # {‘a‘: 10, ‘b‘: 31, ‘c‘: 30, ‘end‘: 60}
    print(parents)  # {‘a‘: ‘start‘, ‘b‘: ‘c‘, ‘c‘: ‘a‘, ‘end‘: ‘c‘}
    print(shortest_way(parents))  # start --> a --> c --> end
    

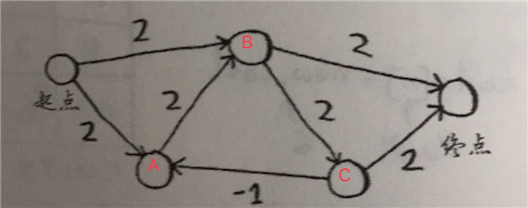
示例4

from 迪克斯特拉算法2_B import shortest_way, inf

grahp = {
    ‘start‘: {
        ‘b‘: 2,
        ‘a‘: 2
    },
    ‘a‘: {
        ‘b‘: 2
    },
    ‘b‘: {
        ‘c‘: 2,
        ‘end‘: 2
    },
    ‘c‘: {
        ‘a‘: -1,
        ‘end‘: 2
    },
    ‘end‘: {}
}
costs = {
    ‘a‘: 2,
    ‘b‘: 2,
    ‘c‘: inf,
    ‘end‘: inf
}
parents = {
    ‘a‘: ‘start‘,
    ‘b‘: ‘start‘,
    ‘c‘: None,
    ‘end‘: None
}
processed = []

def find_lowest_cost_node(costs):
    lowest_node = None
    lowest_node_cost = inf
    for node in costs:
        if lowest_node_cost > costs[node] and node not in processed:
            lowest_node = node
            lowest_node_cost = costs[node]
    return lowest_node

if __name__ == ‘__main__‘:
    node = find_lowest_cost_node(costs)
    while node:
        nighbors = grahp[node]
        for n in nighbors.keys():
            new_cost = costs[node] + nighbors[n]
            if costs[n] > new_cost:
                costs[n] = new_cost
                parents[n] = node
        processed.append(node)
        node = find_lowest_cost_node(costs)

    print(shortest_way(parents))  # start --> b --> end

算法——权重最短路径算法

标签：oat   start   最短路径算法   __name__   com   site   join   process   ESS   

原文地址：https://www.cnblogs.com/pywjh/p/14945404.html