标签:style blog http io color ar os 使用 sp
现在开始学习CORDIC算法
学习的博文:
(1)http://blog.csdn.net/liyuanbhu/article/details/8458769 三角函数计算,Cordic 算法入门
(1)很好的解释了cordic算法的思想。坐标旋转公式。推导http://www.cnblogs.com/ywxgod/archive/2010/08/06/1793609.html
顺时针旋转: x‘ = xcos(θ) + ysin(θ), y‘ = -xsin(θ) + ycos(θ);
逆时针旋转:x‘ = xcos(θ) - ysin(θ), y‘ = xsin(θ) + ycos(θ);
知道这个后,要确定(x,y)的极坐标ρ = sqrt(x2+y2 ), θ = arctan(y/x)。其中θ 的求解就是一个要求超函数。在博文中是通过二分查找发。其中逼近的指标是y = 0;到此我估计cordic算法也是一种类似的逼近。
这个二分查找实在是形象。
使用FPGA实现如下:只使用了5级流水线。其角度精度在26-7.
1 //***************************************************************************************** 2 // 3 // function: achieve the coordinate rotation digital computers 5 4 // 5 // 6 // corn 2014.11.15 7 // 8 // 9 //***************************************************************************************** 10 11 module cordic_module( 12 input clk, rst_n, 13 14 input signed [7 : 0] x0, y0, 15 16 output reg signed [7 : 0] r, syta 17 18 ); 19 20 parameter WIDTH = 8; 21 22 23 reg signed [WIDTH - 1 : 0] x0_r, x1_r, x2_r, x3_r, x4_r; 24 reg signed [WIDTH - 1 : 0] y0_r, y1_r, y2_r, y3_r, y4_r; 25 reg signed [WIDTH - 1 : 0] syta0_r, syta1_r, syta2_r, syta3_r, syta4_r; 26 27 28 always @(posedge clk or negedge rst_n) begin 29 if(!rst_n) begin 30 syta0_r <= 0; 31 end 32 else begin 33 //first stage---------------------------------------------------------- 34 if(x0 >= 0) begin //in the first sector or forth sector 35 x0_r <= x0; 36 y0_r <= y0; 37 syta0_r <= 0; 38 end 39 else if(y0 >= 0) begin //in the second sector 40 x0_r <= y0; 41 y0_r <= -x0; 42 syta0_r <= 90; 43 end 44 else begin //in the third sector 45 x0_r <= -y0; 46 y0_r <= x0; 47 syta0_r <= -90; 48 end 49 //second stage arctan(1)------------------------------------------------------- 50 if(y0_r >= 0) begin 51 x1_r <= x0_r + y0_r; 52 y1_r <= y0_r - x0_r; 53 syta1_r <= syta0_r + 45; 54 end 55 else begin 56 x1_r <= x0_r - y0_r; 57 y1_r <= y0_r + x0_r; 58 syta1_r <= syta0_r - 45; 59 end 60 //third stage arctan(2)--------------------------------------------------------- 61 if(y1_r >= 0) begin 62 x2_r <= x1_r + y1_r / 2; 63 y2_r <= y1_r - x1_r / 2; 64 syta2_r <= syta1_r + 26; 65 end 66 else begin 67 x2_r <= x1_r - y1_r / 2; 68 y2_r <= y1_r + x1_r / 2; 69 syta2_r <= syta1_r - 26; 70 end 71 //forth stage arctan(4)--------------------------------------------------------- 72 if(y2_r >= 0) begin 73 x3_r <= x2_r + y2_r / 4; 74 y3_r <= y2_r - x2_r / 4; 75 syta3_r <= syta2_r + 14; 76 end 77 else begin 78 x3_r <= x2_r - y2_r / 4; 79 y3_r <= y2_r + x2_r / 4; 80 syta3_r <= syta2_r - 14; 81 end 82 //fiveth stage arctan(8)--------------------------------------------------------- 83 if(y3_r >= 0) begin 84 x4_r <= x3_r + y3_r / 8; 85 y4_r <= y3_r - x3_r / 8; 86 syta4_r <= syta3_r + 7; 87 end 88 else begin 89 x4_r <= x3_r - y3_r / 8; 90 y4_r <= y3_r + x3_r / 8; 91 syta4_r <= syta3_r - 7; 92 end 93 94 //output 95 r <= x4_r; 96 syta <= syta4_r; 97 end 98 99 100 101 end //always 102 // 103 104 105 106 endmodule
仿真结果:
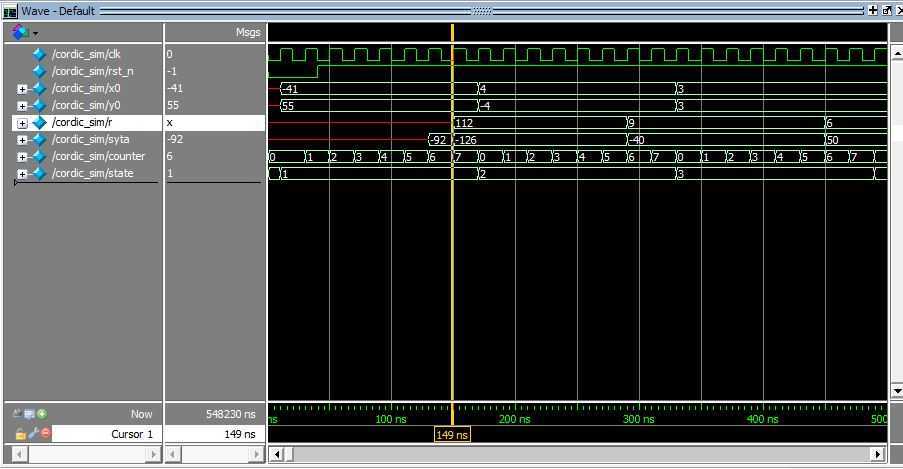
其中使用了三组数据:(-41, 55),(4, -4),(3, 3)
使用计算机的结果:(68.6,-53), (5.6, -45) (4.2, 45)
仿真结果: (112,-126),(9, -40),(6, 50)其中(-126)180 = -54
结论: 半径有所增加,角度有一定的误差误差范围在27-7。在角度的时候有一定的误差。如果要增加精度,就增加迭代的次数。
标签:style blog http io color ar os 使用 sp
原文地址:http://www.cnblogs.com/cornhill/p/4098123.html