标签:android style blog http io ar os 使用 sp
二维码的定义:二维码 (2-dimensional bar code),是用某种特定的几何图形按一定规律在平面(二维方向上)
分布的黑白相间的图形记录数据符号信息的。
在许多种类的二维条码中,常用的码制有:Data Matrix, Maxi Code, Aztec, QR Code, Vericode, PDF417, Ultracode, Code 49, Code 16K等。
1.堆叠式/行排式二维条码,如,Code 16K、Code 49、PDF417(如下图)等
2.矩阵式二维码,最流行莫过于QR CODE
二维码的名称是相对与一维码来说的,比如以前的条形码就是一个“一维码”,
它的优点有:二维码存储的数据量更大;可以包含数字、字符,及中文文本等混合内容;有一定的容错性(在部分损坏以后可以正常读取);空间利用率高等。
二维码原理介绍:QR(Quick-Response) code是被广泛使用的一种二维码,解码速度快。
它可以存储多用类型
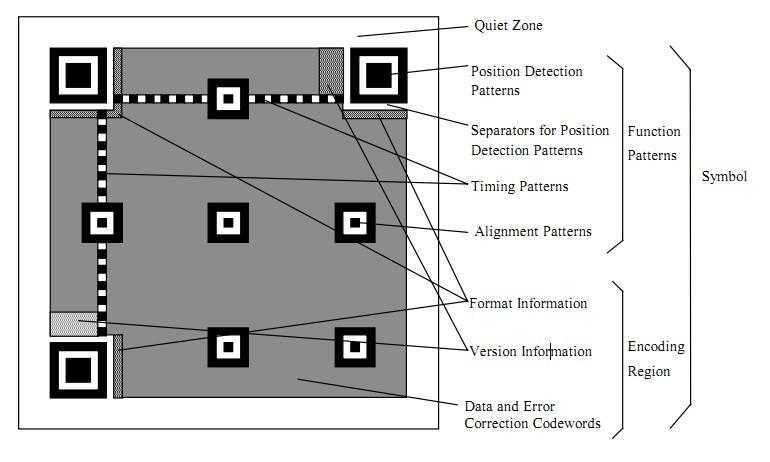
如上图时一个qrcode的基本结构,其中:
位置探测图形、位置探测图形分隔符、定位图形:用于对二维码的定位,对每个QR码来说,位置都是固定存在的,只是大小规格会有所差异;
校正图形:规格确定,校正图形的数量和位置也就确定了;
格式信息:表示改二维码的纠错级别,分为L、M、Q、H;
版本信息:即二维码的规格,QR码符号共有40种规格的矩阵(一般为黑白色),从21x21(版本1),到177x177(版本40),每一版本符号比前一版本 每边增加4个模块。
数据和纠错码字:实际保存的二维码信息,和纠错码字(用于修正二维码损坏带来的错误)。
简要的编码过程:
1. 数据分析:确定编码的字符类型,按相应的字符集转换成符号字符; 选择纠错等级,在规格一定的条件下,纠错等级越高其真实数据的容量越小。
2. 数据编码:将数据字符转换为位流,每8位一个码字,整体构成一个数据的码字序列。其实知道这个数据码字序列就知道了二维码的数据内容。
数据可以按照一种模式进行编码,以便进行更高效的解码,例如:对数据:01234567编码(版本1-H),
1)分组:012 345 67
2)转成二进制:
012→0000001100
345→0101011001
67 →1000011
3)转成序列:0000001100 0101011001 1000011
4)字符数 转成二进制:8→0000001000
5)加入模式指示符(上图数字)0001:0001 0000001000 0000001100 0101011001 1000011
对于字母、中文、日文等只是分组的方式、模式等内容有所区别。基本方法是一致的
3. 纠错编码:按需要将上面的码字序列分块,并根据纠错等级和分块的码字,产生纠错码字,并把纠错码字加入到数据码字序列后面,成为一个新的序列。
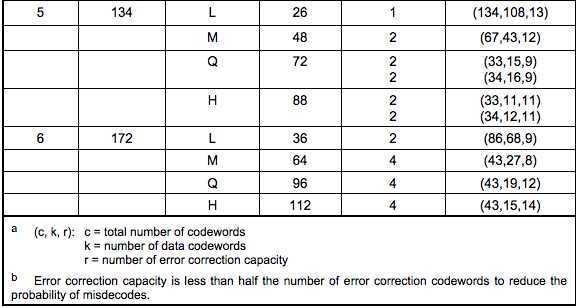
在二维码规格和纠错等级确定的情况下,其实它所能容纳的码字总数和纠错码字数也就确定了,比如:版本10,纠错等级时H时,总共能容纳346个码字,其中224个纠错码字。
就是说二维码区域中大约1/3的码字时冗余的。对于这224个纠错码字,它能够纠正112个替代错误(如黑白颠倒)或者224个据读错误(无法读到或者无法译码),
这样纠错容量为:112/346=32.4%
4. 构造最终数据信息:在规格确定的条件下,将上面产生的序列按次序放如分块中
按规定把数据分块,然后对每一块进行计算,得出相应的纠错码字区块,把纠错码字区块 按顺序构成一个序列,添加到原先的数据码字序列后面。
如:D1, D12, D23, D35, D2, D13, D24, D36, ... D11, D22, D33, D45, D34, D46, E1, E23,E45, E67, E2, E24, E46, E68,...
构造矩阵:将探测图形、分隔符、定位图形、校正图形和码字模块放入矩阵中。
把上面的完整序列填充到相应规格的二维码矩阵的区域中
6. 掩摸:将掩摸图形用于符号的编码区域,使得二维码图形中的深色和浅色(黑色和白色)区域能够比率最优的分布。
7. 格式和版本信息:生成格式和版本信息放入相应区域内。
版本7-40都包含了版本信息,没有版本信息的全为0。二维码上两个位置包含了版本信息,它们是冗余的。
版本信息共18位,6X3的矩阵,其中6位时数据为,如版本号8,数据位的信息时 001000,后面的12位是纠错位。
练习实现二维码编码与解码过程:(调用三方包zxing 其中的解码与编码的API)
编码过程:
public static void encode(String content, String format, String filePath) {
try {
Hashtable hints = new Hashtable();//设置编码类型
hints.put(EncodeHintType.CHARACTER_SET, DEFAULT_ENCODING); //编码
BitMatrix bitMatrix = new QRCodeWriter().encode(content,
BarcodeFormat.QR_CODE, DEFAULT_IMAGE_WIDTH,
DEFAULT_IMAGE_HEIGHT,hints);
//输出到文件,也可以输出到流
File file = new File(filePath);
MatrixToImageWriter.writeToFile(bitMatrix, format, file);
} catch (IOException e) {
e.printStackTrace();
} catch (WriterException e1) {
e1.printStackTrace();
}
}
解码过程:
BufferedImage image = ImageIO.read(file);//读取文件
LuminanceSource source = new BufferedImageLuminanceSource(image);
BinaryBitmap bitmap = new BinaryBitmap(new HybridBinarizer(
source));
//解码
Result result = new MultiFormatReader().decode(bitmap);
String resultStr = result.getText();
System.out.println(resultStr);
二维码又称 QR Code,QR 全称 Quick Response,是一个近几年来移动设备上超流行的一种编码方式,它比传统的 Bar Code 条形码能存更多的信息,也能表示更多的数据类型:比如:字符,数字,日文,中文等等。这两天学习了一下二维码图片生成的相关细节,觉得这个玩意就是一个密码算法,在此写一这篇文章 ,揭露一下。供好学的人一同学习之。
关于 QR Code Specification,可参看这个 PDF:http://raidenii.net/files/datasheets/misc/qr_code.pdf
基础知识
首先,我们先说一下二维码一共有 40 个尺寸。官方叫版本 Version。Version 1 是 21 x 21 的矩阵,Version 2 是 25 x 25 的矩阵,Version 3 是 29 的尺寸,每增加一个 version,就会增加 4 的尺寸,公式是:(V-1)*4 + 21(V是版本号) 最高 Version 40,(40-1)*4+21 = 177,所以最高是 177 x 177 的正方形。
下面我们看看一个二维码的样例:
定位图案
功能性数据
数据码和纠错码
数据编码
我们先来说说数据编码。QR 码支持如下的编码:
Numeric mode 数字编码,从 0 到9。如果需要编码的数字的个数不是 3 的倍数,那么,最后剩下的 1 或 2 位数会被转成 4 或 7bits,则其它的每 3 位数字会被编成 10,12,14bits,编成多长还要看二维码的尺寸(下面有一个表 Table 3 说明了这点)
Alphanumeric mode 字符编码。包括 0-9,大写的A到Z(没有小写),以及符号$ % * + – . / : 包括空格。这些字符会映射成一个字符索引表。如下所示:(其中的 SP 是空格,Char 是字符,Value 是其索引值) 编码的过程是把字符两两分组,然后转成下表的 45 进制,然后转成 11bits 的二进制,如果最后有一个落单的,那就转成 6bits 的二进制。而编码模式和字符的个数需要根据不同的 Version 尺寸编成9, 11 或 13 个二进制(如下表中 Table 3)
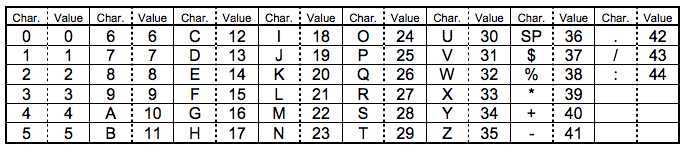
Byte mode, 字节编码,可以是0-255 的 ISO-8859-1 字符。有些二维码的扫描器可以自动检测是否是 UTF-8 的编码。
Kanji mode 这是日文编码,也是双字节编码。同样,也可以用于中文编码。日文和汉字的编码会减去一个值。如:在 0X8140 to 0X9FFC 中的字符会减去 8140,在 0XE040 到 0XEBBF 中的字符要减去 0XC140,然后把前两位拿出来乘以 0XC0,然后再加上后两位,最后转成 13bit 的编码。如下图示例:

Extended Channel Interpretation (ECI) mode 主要用于特殊的字符集。并不是所有的扫描器都支持这种编码。
Structured Append mode 用于混合编码,也就是说,这个二维码中包含了多种编码格式。
FNC1 mode 这种编码方式主要是给一些特殊的工业或行业用的。比如 GS1 条形码之类的。
简单起见,后面三种不会在本文中讨论。
下面两张表中,
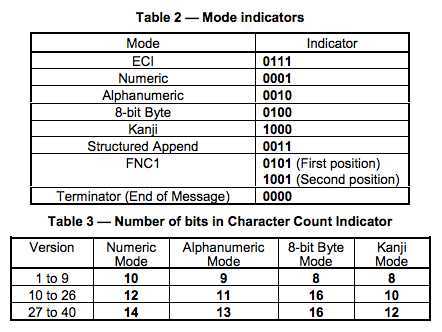
下面我们看几个示例,
示例一:数字编码
在 Version 1 的尺寸下,纠错级别为H的情况下,编码: 01234567
1. 把上述数字分成三组: 012 345 67
2. 把他们转成二进制: 012 转成 0000001100; 345 转成 0101011001; 67 转成 1000011。
3. 把这三个二进制串起来: 0000001100 0101011001 1000011
4. 把数字的个数转成二进制 (version 1-H 是 10 bits ): 8 个数字的二进制是 0000001000
5. 把数字编码的标志 0001 和第 4 步的编码加到前面: 0001 0000001000 0000001100 0101011001 1000011
示例二:字符编码
在 Version 1 的尺寸下,纠错级别为H的情况下,编码: AC-42
1. 从字符索引表中找到 AC-42 这五个字条的索引 (10,12,41,4,2)
2. 两两分组: (10,12) (41,4) (2)
3. 把每一组转成 11bits 的二进制:
(10,12) 10*45+12 等于 462 转成 00111001110
(41,4) 41*45+4 等于 1849 转成 11100111001
(2) 等于 2 转成 000010
4. 把这些二进制连接起来:00111001110 11100111001 000010
5. 把字符的个数转成二进制 (Version 1-H 为 9 bits ): 5 个字符,5 转成 000000101
6. 在头上加上编码标识 0010 和第 5 步的个数编码: 0010 000000101 00111001110 11100111001 000010
结束符和补齐符
假如我们有个 HELLO WORLD 的字符串要编码,根据上面的示例二,我们可以得到下面的编码,
注:二维码的纠错码主要是通过 Reed-Solomon error correction(里德-所罗门纠错算法)来实现的。对于这个算法,对于我来说是相当的复杂,里面有很多的数学计算,比如:多项式除法,把1-255 的数映射成 2 的n次方(0<=n<=255)的伽罗瓦域 Galois Field 之类的神一样的东西,以及基于这些基础的纠错数学公式,因为我的数据基础差,对于我来说太过复杂,所以我一时半会儿还有点没搞明白,还在学习中,所以,我在这里就不展开说这些东西了。还请大家见谅了。(当然,如果有朋友很明白,也繁请教教我)
最终编码
穿插放置
如果你以为我们可以开始画图,你就错了。二维码的混乱技术还没有玩完,它还要把数据码和纠错码的各个 codewords 交替放在一起。如何交替呢,规则如下:
对于数据码:把每个块的第一个 codewords 先拿出来按顺度排列好,然后再取第一块的第二个,如此类推。如:上述示例中的 Data Codewords 如下:
| 块 1 | 67 | 85 | 70 | 134 | 87 | 38 | 85 | 194 | 119 | 50 | 6 | 18 | 6 | 103 | 38 | |
| 块 2 | 246 | 246 | 66 | 7 | 118 | 134 | 242 | 7 | 38 | 86 | 22 | 198 | 199 | 146 | 6 | |
| 块 3 | 182 | 230 | 247 | 119 | 50 | 7 | 118 | 134 | 87 | 38 | 82 | 6 | 134 | 151 | 50 | 7 |
| 块 4 | 70 | 247 | 118 | 86 | 194 | 6 | 151 | 50 | 16 | 236 | 17 | 236 | 17 | 236 | 17 | 236 |
我们先取第一列的:67, 246, 182, 70
然后再取第二列的:67, 246, 182, 70, 85,246,230 ,247
如此类推:67, 246, 182, 70, 85,246,230 ,247 ……… ……… ,38,6,50,17,7,236
对于纠错码,也是一样:
| 块 1 | 213 | 199 | 11 | 45 | 115 | 247 | 241 | 223 | 229 | 248 | 154 | 117 | 154 | 111 | 86 | 161 | 111 | 39 |
| 块 2 | 87 | 204 | 96 | 60 | 202 | 182 | 124 | 157 | 200 | 134 | 27 | 129 | 209 | 17 | 163 | 163 | 120 | 133 |
| 块 3 | 148 | 116 | 177 | 212 | 76 | 133 | 75 | 242 | 238 | 76 | 195 | 230 | 189 | 10 | 108 | 240 | 192 | 141 |
| 块 4 | 235 | 159 | 5 | 173 | 24 | 147 | 59 | 33 | 106 | 40 | 255 | 172 | 82 | 2 | 131 | 32 | 178 | 236 |
和数据码取的一样,得到:213,87,148,235,199,204,116,159,…… …… 39,133,141,236
然后,再把这两组放在一起(纠错码放在数据码之后)得到:
67, 246, 182, 70, 85, 246, 230, 247, 70, 66, 247, 118, 134, 7, 119, 86, 87, 118, 50, 194, 38, 134, 7, 6, 85, 242, 118, 151, 194, 7, 134, 50, 119, 38, 87, 16, 50, 86, 38, 236, 6, 22, 82, 17, 18, 198, 6, 236, 6, 199, 134, 17, 103, 146, 151, 236, 38, 6, 50, 17, 7, 236, 213, 87, 148, 235, 199, 204, 116, 159, 11, 96, 177, 5, 45, 60, 212, 173, 115, 202, 76, 24, 247, 182, 133, 147, 241, 124, 75, 59, 223, 157, 242, 33, 229, 200, 238, 106, 248, 134, 76, 40, 154, 27, 195, 255, 117, 129, 230, 172, 154, 209, 189, 82, 111, 17, 10, 2, 86, 163, 108, 131, 161, 163, 240, 32, 111, 120, 192, 178, 39, 133, 141, 236
Remainder Bits
最后再加上 Reminder Bits,对于某些 Version 的 QR,上面的还不够长度,还要加上 Remainder Bits,比如:上述的 5Q 版的二维码,还要加上 7 个 bits,Remainder Bits 加零就好了。关于哪些 Version 需要多少个 Remainder bit,可以参看 QR Code Spec 的第 15 页的 Table-1 的定义表。
画二维码图
Position Detection Pattern
首先,先把 Position Detection 图案画在三个角上。
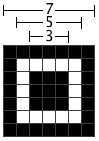
Alignment Pattern
然后,再把 Alignment 图案画上

关于 Alignment 的位置,可以查看 QR Code Spec 的第 81 页的 Table-E.1 的定义表(下表是不完全表格)
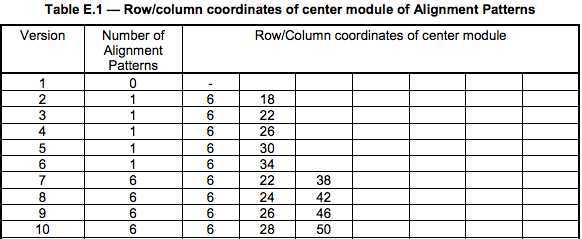
下图是根据上述表格中的 Version8 的一个例子(6,24,42)
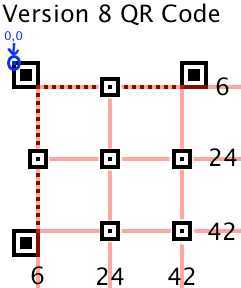
Timing Pattern
接下来是 Timing Pattern 的线(这个不用多说了)
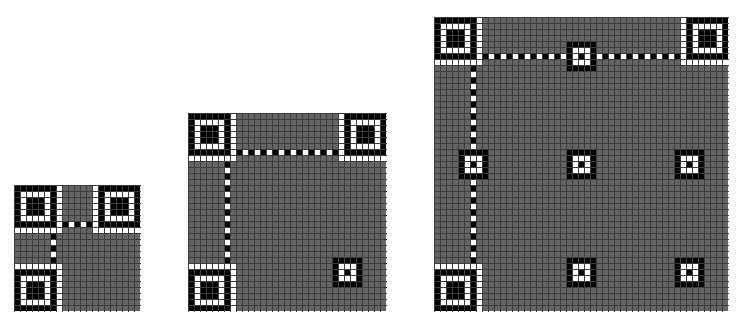
Format Information
再接下来是 Formation Information,下图中的蓝色部分。
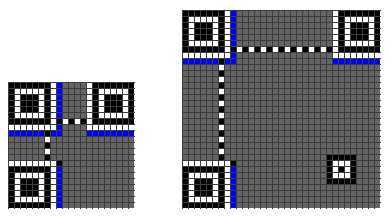
Format Information 是一个 15 个 bits 的信息,每一个 bit 的位置如下图所示:(注意图中的 Dark Module,那是永远出现的)
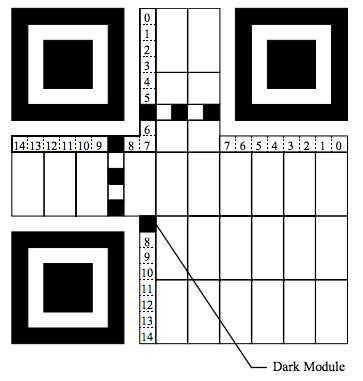
这 15 个 bits 中包括:
然后 15 个 bits 还要与 101010000010010 做 XOR 操作。这样就保证不会因为我们选用了 00 的纠错级别,以及 000 的 Mask,从重造成全部为白色,这会增加我们的扫描器的图像识别的困难。
下面是一个示例:

关于 Error Correction Level 如下表所示:
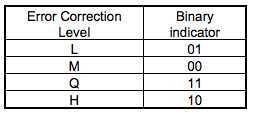
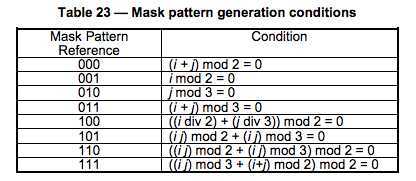
关于 Mask 图案如后面的 Table 23 所示。
Version Information
再接下来是 Version Information(版本 7 以后需要这个编码),下图中的蓝色部分。
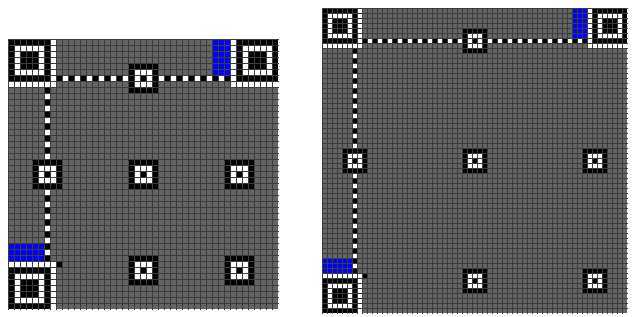
Version Information 一共是 18 个 bits,其中包括 6 个 bits 的版本号以及 12 个 bits 的纠错码,下面是一个示例:

而其填充位置如下:
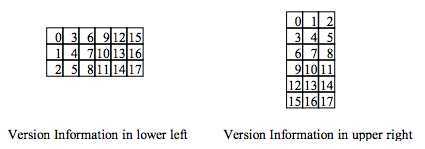
数据和数据纠错码
然后是填接我们的最终编码,最终编码的填充方式如下:从左下角开始沿着红线填我们的各个 bits,1 是黑色,0 是白色。如果遇到了上面的非数据区,则绕开或跳过。

掩码图案
这样下来,我们的图就填好了,但是,也许那些点并不均衡,所以,我们还要做 Masking 操作(靠,还嫌不复杂)QR 的 Spec 中说了,QR 有 8 个 Mask 你可以使用,如下所示:其中,各个 mask 的公式在各个图下面。所谓 mask,说白了,就是和上面生成的图做 XOR 操作。Mask 只会和数据区进行 XOR,不会影响功能区。

其 Mask 的标识码如下所示:(其中的i,j分别对应于上图的x,y)
下面是 Mask 后的一些样子,我们可以看到被某些 Mask XOR 了的数据变得比较零散了。
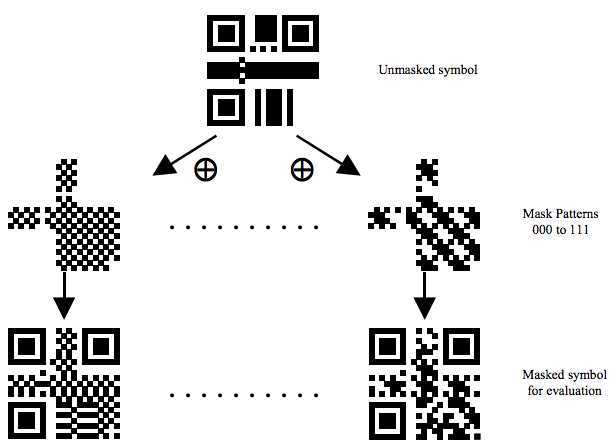
Mask 过后的二维码就成最终的图了。
可以去尝试去写一下 QR 的编码程序,当然,你可以用网上找个 Reed Soloman 的纠错算法的库,或是看看别人的源代码是怎么实现这个繁锁的编码。
标签:android style blog http io ar os 使用 sp
原文地址:http://www.cnblogs.com/douzhanshen/p/4126362.html