标签:style blog http io ar color os sp for
由于这个是K-means的改进算法,所以优缺点与之相同。
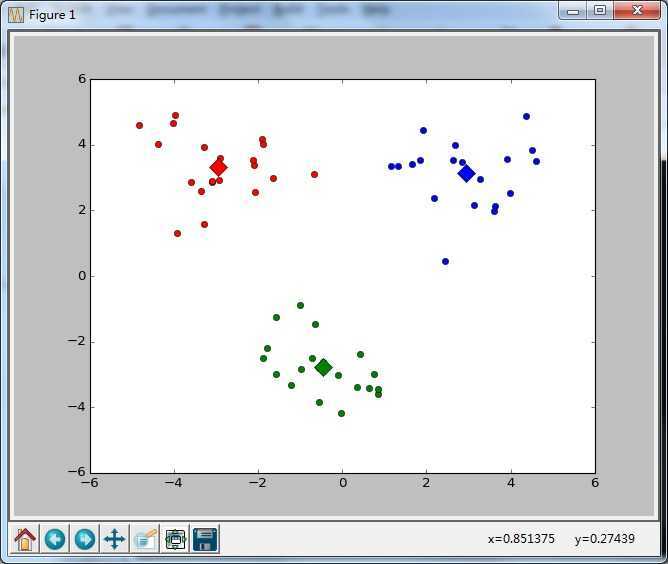
1.要了解这个首先应该了解K-means算法,可以看这里这个算法的思想是:首先将所有点作为一个簇,然后将该簇一分为二。之后选择能最大程度降低聚类代价函数(也就是误差平方和)的簇划分为两个簇(或者选择最大的簇等,选择方法多种)。以此进行下去,直到簇的数目等于用户给定的数目k为止。
2.以上隐含着一个原则是:因为聚类的误差平方和能够衡量聚类性能,该值越小表示数据点月接近于它们的质心,聚类效果就越好。所以我们就需要对误差平方和最大的簇进行再一次的划分,因为误差平方和越大,表示该簇聚类越不好,越有可能是多个簇被当成一个簇了,所以我们首先需要对这个簇进行划分。
3.关于二分K-means的优点《Machine Learning in Action》说的是能够克服K-means收敛于局部最小,但是想了一下感觉这个并不能保证收敛到全局最优值(而且后面运行代码结果也会出现不太好的情况,不知道这算不算是个证据)
4.通过查阅一些资料和总结,二分K-means聚类的优点有:
所以说这个算法也并不能够保证完全不受K的影响一定归到全局最小,只是相对较优,并且还有了一定的速度提升。理解有偏差欢迎指正。
biKmeans(dataSet, k, distMeas=distEclud)
这个函数实现了二分算法,过程大体如下(代码中注释已经很详细了):
1.初始化全部点的质心,并建立所需要的数据存储结构
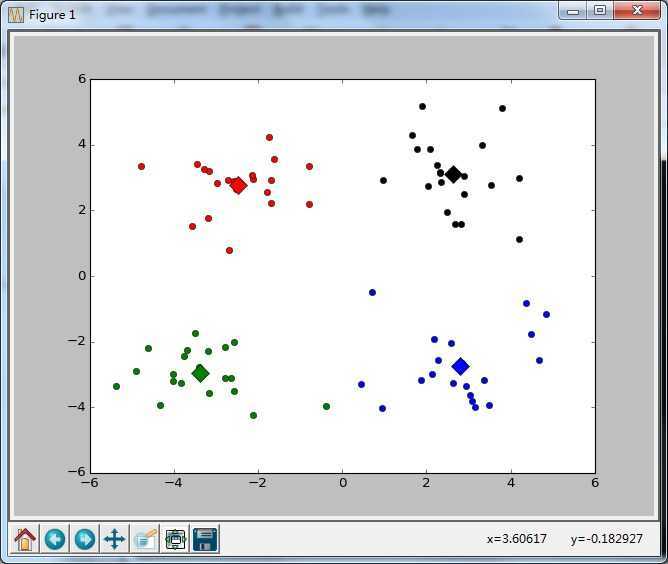
2.对每一个簇尝试二分(最开始就是一个簇),选出最好的
3.更新各个簇的元素个数
1 def biKmeans(dataSet, k, distMeas=distEclud): 2 m = shape(dataSet)[0] 3 clusterAssment = mat(zeros((m,2)))#记录簇分配的结果及误差 4 centroid0 = mean(dataSet, axis=0).tolist()[0]#计算整个数据集的质心 5 centList =[centroid0] #create a list with one centroid 6 for j in range(m):#计算初始聚类点与其他点的距离 7 clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2 8 while (len(centList) < k): 9 lowestSSE = inf 10 for i in range(len(centList)):#尝试划分每一簇 11 ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]#get the data points currently in cluster i 12 centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)#对这个簇运行一个KMeans算法,k=2 13 sseSplit = sum(splitClustAss[:,1])#compare the SSE to the currrent minimum 14 sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1]) 15 print "sseSplit, and notSplit: ",sseSplit,sseNotSplit 16 if (sseSplit + sseNotSplit) < lowestSSE:##划分后更好的话 17 bestCentToSplit = i 18 bestNewCents = centroidMat 19 bestClustAss = splitClustAss.copy() 20 lowestSSE = sseSplit + sseNotSplit 21 bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) #更新簇的分配结果change 1 to 3,4, or whatever 22 bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit 23 print ‘the bestCentToSplit is: ‘,bestCentToSplit 24 print ‘the len of bestClustAss is: ‘, len(bestClustAss) 25 centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]#replace a centroid with two best centroids 26 centList.append(bestNewCents[1,:].tolist()[0]) 27 clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss#reassign new clusters, and SSE 28 return mat(centList), clusterAssment
标签:style blog http io ar color os sp for
原文地址:http://www.cnblogs.com/MrLJC/p/4129700.html