标签:style blog http io ar color os 使用 sp
B 树(B-Tree)是为磁盘等辅助存取设备设计的一种平衡查找树,它实现了以 O(log n) 时间复杂度执行查找、顺序读取、插入和删除操作。由于 B 树和 B 树的变种在降低磁盘 I/O 操作次数方面表现优异,所以经常用于设计文件系统和数据库。
在 1972 年,在 Boeing Research Labs 工作的 Rudolf Bayer 和 Ed McCreight 发明了 B 树。当时他们并没有解释 B 树中的 "B" 代表什么涵义,所以猜测的多是 "Balanced", "Broad", "Bushy", "Boeing", "Bayer" 等,不过通常使用 "Balanced" 来描述树是平衡的。Ed McCreight 在 CPM 2013 会议中回答 "B" 的起源问题时说:"对 B 的涵义思考的越多,对 B 树的理解则越深。"。
如下图是一棵键值为英语字母的 B 树,带浅阴影的节点是查找字母 R 时要检查的节点。
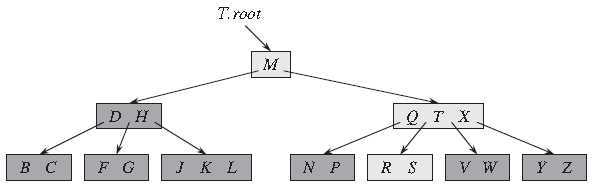
B 树中的节点分为内部节点(Internal Node)和叶节点(Leaf Node),内部节点也就是非叶节点(Non-Leaf Node)。
B 树的内部节点可以包含 2 个以上的子节点,所以在设计时可以预先设定可包含子节点的数量范围,也就是上界(Upper Bound)和下界(Lower Bound)。当向节点插入或删除数据时,也就意味着子节点的数量发生变化。为了维持在预先设定的数量范围,内部节点可能会被合并(Join)或拆分(Split)。因为子节点的数量有一定的范围,所以 B 树不需要频繁地变化以保持平衡。但同时,由于节点可能没有被完全填充,所以会浪费一些空间。
B 树中每一个内部节点会包含一定数量的键值(Key)。这些键值同时也扮演着分割子节点的角色。例如,假设某内部节点包含 3 个子节点,则实际上必须有 2 个键值:a1 和 a2。其中,a1 的左子树上的所有的值都要小于 a1,在 a1 和 a2 之间的子树中的值都大于 a1 并小于 a2,a2 的右子树上的所有的值都大于 a2。
通常,键值的数量被设定在 d 和 2d 之间,其中 d 是可包含键值的最小数量。可知,d + 1 是节点可拥有子节点的最小数量,也就是树的最小的度(Degree)。因数 2 将确保节点可以被合并或拆分。
如果一个内部节点有 2d 个键值,那么添加一个键值给该节点将会导致 2d + 1 的数量大于范围上界,则会拆分 2d + 1 数量的节点为 2 个 d 数量的节点,并有 1 个键值提升至父节点中。
类似地,如果一个内部节点和它的邻居节点(Neighbor)都包含 d 个键值,那么删除一个键值将导致此节点拥有 d - 1 个键值,小于范围下界,则会导致与邻居节点合并。合并后的节点包括 d – 1 的数量加上邻居的 d 的数量和两者的父节点中的 1 个键值,共为 d – 1 + d + 1 = 2d 数量的节点。
深度(Depth)描述树中层(Level)的数量。B 树通过要求所有叶节点保持在相同深度来保持树的平衡。深度通常会随着键值的不断添加而缓慢地增长。
对于 B 树定义中的一些术语常有混淆,比如对于阶(Order)的定义。Knuth Donald 在 1998 年将阶(Order)定义为节点包含子节点的最大数量。
使用阶来定义 B 树,一棵 m 阶的 B 树,需要满足下列条件:
下面是一棵高度(Height)为 3 的 B 树。
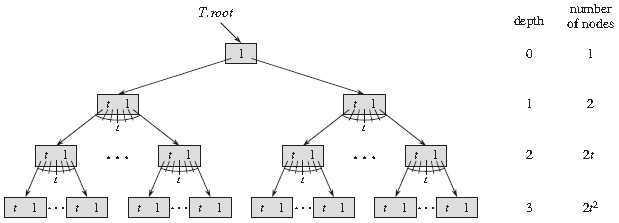
B 树上大部分操作所需的磁盘存取次数与 B 树的高度成正比。
使用 h 代表 B 树的高度;使用 n 代表整个树中包含键值的数量 n > 0;m 为内部节点可包含子节点的最大数量,则当树满时 n = mh – 1;每个内部节点最多包含 m - 1 个键值;使用 d 代表内部节点可包含最少子节点的数量,即最小度数(Degree)有 d = ⌈m/2⌉。
B 树的最优条件下的 h 为:
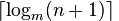
B 树的最差条件下的 h 为:
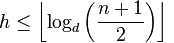
合理的选取最小度数 d 的值,可以大大地降低树的高度,则可降低查找任意键值时所需的磁盘存取次数。与自平衡二叉树相比,高度都以 O(log n) 的速度增长,对 B 树来说对数的底要大很多倍。对于大多数树操作来说,B 树要比自平衡二叉树节省大约 lg d 因子的节点检查次数。因为在树中查找任意一个节点通常都需要一次磁盘存取,所以磁盘存取的次数大大地减少了。
查询操作
在 B 树中查询键值与在二叉树中的键值查询方式是类似的。从根节点开始查询,通过递归进行自顶向下的遍历。在每一层上,将查询键值与内部节点中的键值比较,以确定向哪个子树中进行遍历。
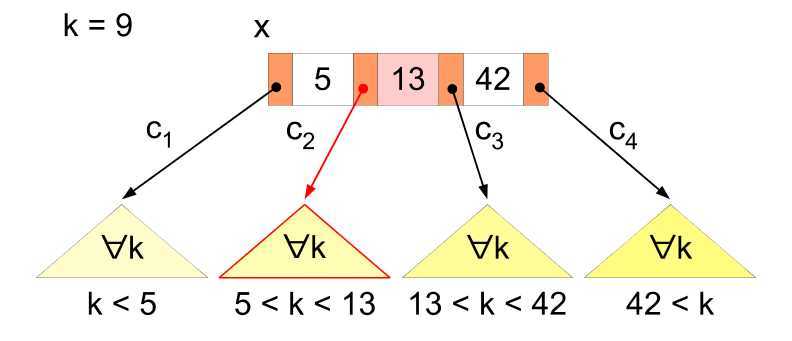
二叉树相关的查询可参考如下文章:
插入操作
当要插入一个新的键值时,首先在树中找到该键值应当被插入的叶节点的位置:
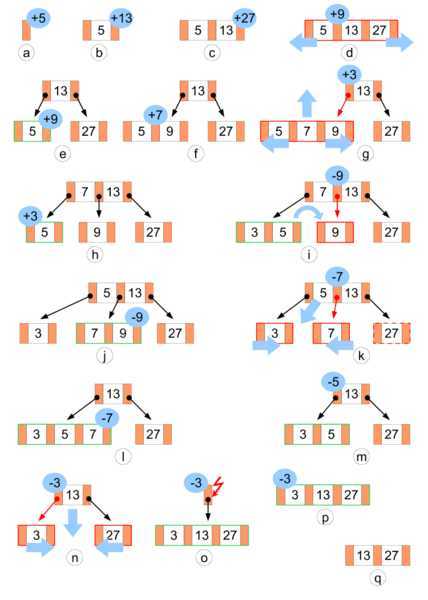
删除操作
在 B 树中删除键值可以通过不同的策略来实现,这里介绍常见的定位删除策略:定位键值后删除,然后重构整个树至平衡。平衡指的是仍然保持 B 树的性质。
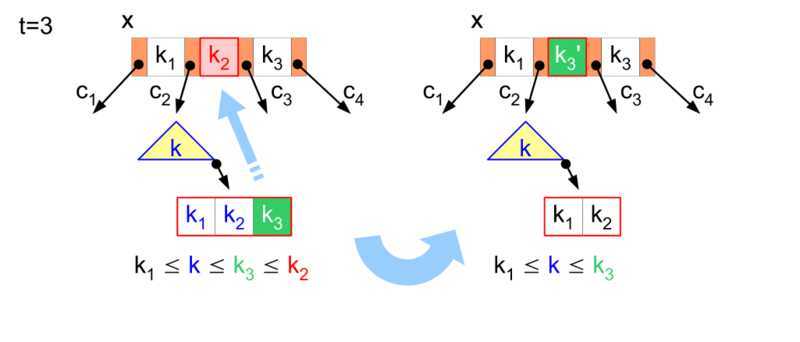
"B 树" 这个术语在实际应用中还代表着多种 B 树的变种,它们有着相似的结构,却各有特点和优势:
B+ 树是 B 树的一个变种,在内部节点中存储的键值同样也会出现在叶节点中,但内部节点中不存储关联附属数据或指针。在叶节点中的不仅存储键值,还存储关联附属数据或指针。这样,所有的附属数据都保存在了叶节点中,只将键值和子女指针保存在了内节点中,因此最大化了内节点的分支能力。
此外,叶节点还增加了一个指向下一个顺序关联叶节点的指针,以改进顺序读取的速度。
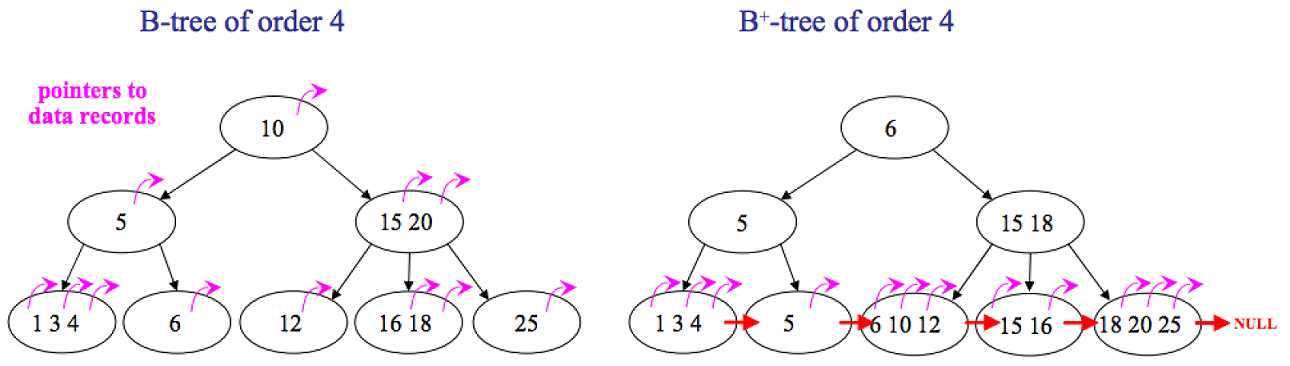
常见的文件系统和数据库均使用 B+ 树实现,例如:
B+ 树的优势在于:
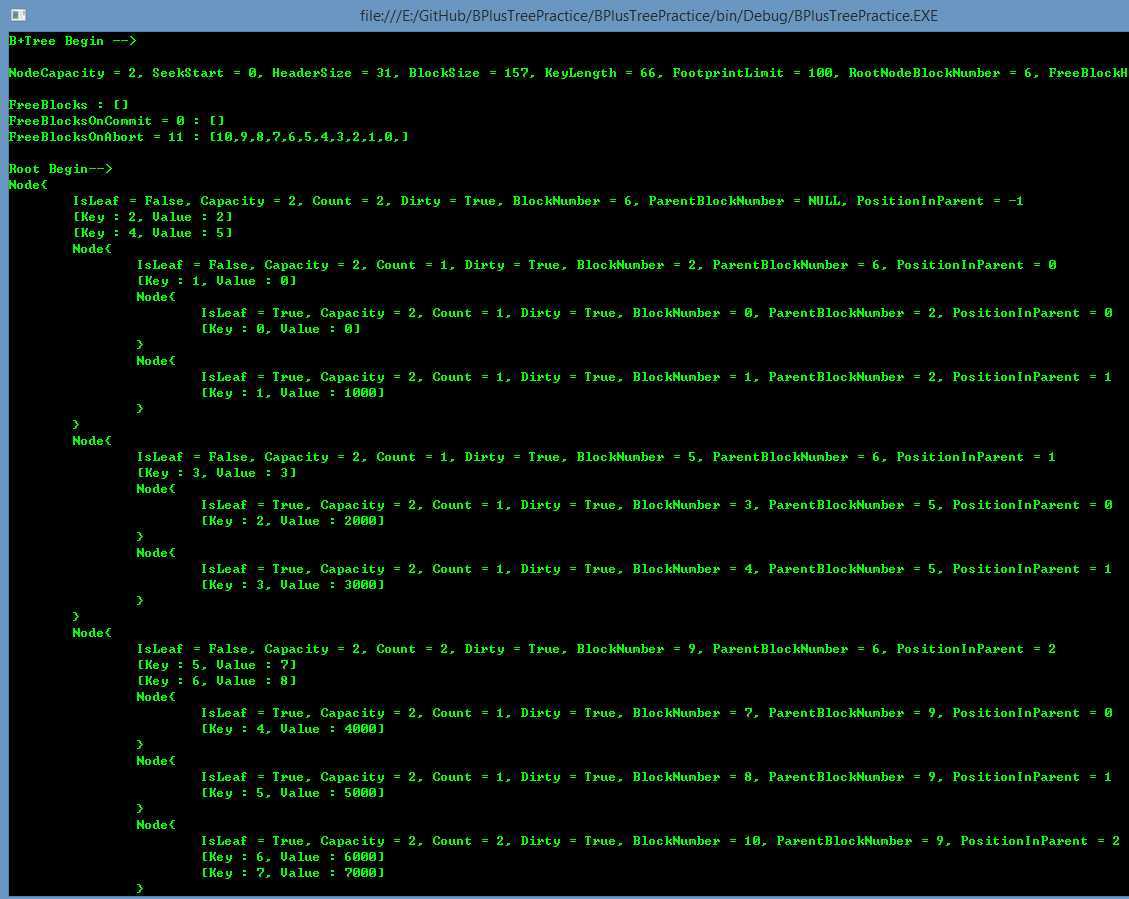
在 GitHub 上的项目 BPlusTreePractice 使用 C# 语言实现了简单的 B+ 树,功能包括插入键值对、搜索键、删除键、存储至磁盘块文件等,但未实现节点链的双向链表和扫描功能。
下面是测试代码示例。
1 using System; 2 using System.IO; 3 4 namespace BPlusTreePractice 5 { 6 class Program 7 { 8 static void Main(string[] args) 9 { 10 // 指定磁盘文件位置 11 string treeFileName = 12 @"E:\BPlusTree_" + DateTime.Now.ToString(@"yyyyMMddHHmmssffffff") + ".data"; 13 Stream treeFileStream = 14 new FileStream(treeFileName, FileMode.CreateNew, FileAccess.ReadWrite); 15 16 // 初始化 B+ 树,固定长度字符串为键,映射至长整形 17 int keyLength = 64; 18 int nodeCapacity = 2; 19 BPlusTree tree = 20 BPlusTree.InitializeInStream(treeFileStream, 0L, keyLength, nodeCapacity); 21 22 // 插入 0 到 7 共 8 个键值对 23 for (int i = 0; i < 8; i++) 24 { 25 tree.Set(i.ToString(), (long)(i * 1000)); // Key 是字符串,Value 是 long 类型 26 } 27 28 // 将 B+ 树输出到命令行 29 Console.WriteLine(tree.ToText()); 30 31 // 获取指定的键值对 32 Console.WriteLine(); 33 Console.WriteLine(string.Format("Tree‘s first key is {0}.", tree.FirstKey())); 34 Console.WriteLine(string.Format("Check key {0} exists {1}.", 35 "3", tree.ContainsKey("3"))); 36 Console.WriteLine(string.Format("{0}‘s next key is {1}.", "6", tree.NextKey("6"))); 37 Console.WriteLine(string.Format("Get key {0} with value {1}.", "2", tree.Get("2"))); 38 Console.WriteLine(string.Format("Index key {0} with value {1}.", "4", tree["4"])); 39 Console.WriteLine(); 40 41 // 删除键值对 42 tree.RemoveKey("6"); 43 Console.WriteLine(tree.ToText()); 44 45 Console.ReadKey(); 46 } 47 } 48 }
本篇文章《B 树和 B+ 树》由 Dennis Gao 发表自博客园个人技术博客,未经作者本人同意禁止任何形式的转载,任何自动或人为的爬虫转载或抄袭行为均为耍流氓。
标签:style blog http io ar color os 使用 sp
原文地址:http://www.cnblogs.com/gaochundong/p/btree_and_bplustree.html