标签:希尔排序
(摘自wiki) 一个更好理解的希尔排序实现:将数组列在一个表中并对列排序。重复这过程,不过每次用更长的列来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法,算法本身仅仅对原数组进行排序(通过增加索引的步长,例如是用i
+= step_size而不是i++)。
例如,假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ],如果我们以步长为5开始进行排序,我们可以通过将这列表放在有5列的表中来更好地描述算法,这样他们就应该看起来是这样:
13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10
然后我们对每列进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
将上述四行数字,依序接在一起时我们得到:[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时10已经移至正确位置了,然后再以3为步长进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
排序之后变为:
10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94
最后以1步长进行排序(此时就是简单的插入排序了)。
#include<iostream>
using namespace std;
void shellsort(int a[],int N)//希尔排序
{
int gap;
int tmp;
int p;
int j;
for (gap = N/2; gap > 0; gap = gap/2)//这里采用的是最原始的步长1/2
for ( p = gap; p < N ; p++)
{
tmp = a[p];
for (j = p; j >= gap && tmp < a[j- gap]; j = j - gap)
a[j] = a[j-gap];
a[j] = tmp;
}
}
int main()
{
int a[]={54,3,2,1,-9};
shellsort(a , 5);
for(int i=0;i<sizeof(a)/sizeof(int);++i)
printf("%d\n",a[i]);
}

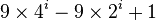 和
和  这两个算式
这两个算式标签:希尔排序
原文地址:http://blog.csdn.net/wdkirchhoff/article/details/41808563