七牛的存储算法猜测

    个人浏览网页的时候，有打标签的习惯。最近整理以往的标签的时候，发现积累了一些有关七牛公司存储策略的网页，遂决定整理一篇文章处理，以备记忆。当然，也希望对他人有用。

    因为七牛公司的存储策略主要基于纠删码(Erasure Codes,EC)，所以下面先从纠删码引申开来。

引言：何为纠删码

    数据的爆炸式增长使得存储系统的规模不断增加，存储设备的可靠性却一直没有得到显著提高（SSD 从SLC 到MLC 和TLC 可靠性不断下降，磁盘随着单位面积写入数据更多导致可靠性无法提升），从而给数据的持久化存储带来巨大挑战。另外随着存储系统规模的增大，存储系统中的冷数据的增加将远超过热数据的增加，如何安全保存冷数据，在需要的时候能够获取冷数据也成为存储系统中的重要挑战。

    副本策略和编码策略是保证数据冗余度的两个重要方法。当原始数据发生部分丢失时，副本策略和编码策略都可以保证数据仍旧可以正确获取。副本策略将原始数据拷贝一份或多份进行存储，编码策略则将原始数据分块并编码生成冗余数据块，保证丢失一定量内的数据块，原始数据仍旧可以获取。

    两种策略性能比较如下：

||策略||存储效率||计算开销||修复效率||

||副本策略||低||无||高||

||编码策略||高||有||低||

    虽然编码策略比副本策略存在计算开销和修复效率低（后面将介绍）的缺点，但能够极大的减少存储开销的优势还是为编码策略赢得了巨大的空间。实际中，存在着副本策略和编码策略的存储系统，比如在分布存储系统（HDFS, GFS, TFS）中热数据往往通过副本策略保存，冷数据则通过编码后保存，节省存储空间。在ECC内存和SSD的page 中也使用了ECC 编码策略保证数据冗余。

从信息论和编码的角度来说，纠删码属于分组线性编码。其编码过程可以通过一个编码矩阵GM 和分块数据的乘法（点积）来表示，也就是说编码矩阵GM 定义了数据是如何编码为冗余数据的。 
                                                                              

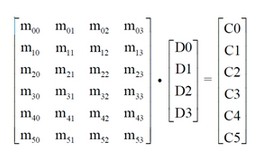
    C0 ~ C5 是冗余数据，所有的冗余数据可以表示为GM × D{D0、D1、D2、D3} 的乘法，每一个冗余数据块Ci 是矩阵的对应的一行和数据块的乘积（黄色标示）。编码矩阵中GM 每一个元素则是对应原始数据块的乘法系数。

    以上摘自：存储系统中的纠删码（Erasure Codes）—综述（一）

纠删码中运算的基础域———有限域

• 什么是有限域?

    在数学上，构建一些符号，和基于它们的运算，构成了一个“域”。如整数数字及其之上的思则运算（加减乘除）构成了一个整数域。如果域中的符号数目是有限的，则称之为有限域，否则即为无限域。如整数域即为无限域，而我们熟悉的布尔域即为有限域。有限域的大小是素数（记作p）或者素数的指数幂（p^q）。

• 域的运算性质
  • 加法和乘法的封闭性，加法和乘法结果还在域内
  • 加法和乘法的交换律； a + b = b + a 和 a · b = b · a
  • 加法和乘法的分配律： a + ( b + c ) = ( a + b ) + c 和 a · ( b · c ) = ( a · b ) · c
  • 加法和乘法的分配律： a · ( b + c ) = ( a · b ) + ( a · c )
  • 存在加法和乘法的单位元素：a+0 = a 和 a·1 = 1（这里的0,1 不是自然数的0,1，代表着域上的加法单位元素和乘法单位元素）
  • 每个域上的元素都存在其负元和逆元： a+(-a) = 0, a·(a -1 ) = 1
• 计算机运算与有限域

    如大家知道的每种计算机语言，不论静态语言还是动态语言，都有其最基本的数据类型，每种数据类型都有其数据范围，这就决定了其间的运算必定是有限域运算。有限域由数学家伽罗瓦最早提出的，一种有限域的构造方法即使由他提出的，也称作Galois Field，这样的域记作GF(p) 和GF(p^{q)，计算机中的p为2，因为其数据是二进制形式，其运算也是基于二进制的运算，即GF(2}w)，w可为1、2、4、8、16等。如果w为1，则GF(2)的加法运算即为异或运算，乘法运算即为与运算。当w大于1时，其加法运算仍未异或预算，而乘法运算则稍有不同，在此不再详解。

七牛的存储方案

• 【先锋】七牛云存储：三年磨一剑及背后核心技术解析

在技术上存储系统的核心诉求是成本和可靠性，而这两者又是一对矛盾，想降低丢失数据的风险，势必要增加每份数据拷贝的份数，而增加每份数据拷贝的份数，又势必增加成本，七牛使用EC冗余算法来平衡这对矛盾。这个算法将一份数据拆分成M份，并将这M份数据代入一个多元线性方程组，算出N份校验数据，然后将这M+N份数据存储，在存储下来的M+N份数据中，有任何一份或多份数据损坏，我们都可以通过这个多元线性方程组将损坏的数据算回，由这个原理我们很容易得到一个结论，使用EC冗余算法的系统最多支持N份数据损毁而不丢失数据，七牛使用了一些自己独有的技术，将M和N都做到比较大的数值，M又远远大于N，使得系统的备份数非常低 — (M+N)/M （M远大于N），而可靠性又非常高 — 可同时损坏N份数据（N也是较大的数值）。我前面讲过七牛使用EC冗余算法，获得了极高的数据可靠性，并在此基础上又引入双数据中心互备来避免单机房灾难性事故，通过这些努力，七牛做到保护企业的数据零丢失。

• 许式伟：十一年逆流顺流，首席架构师到CEO

域代数遵循自然代数的加减乘除规律，但数据值控制在有限区域，不管怎么算，结果都在0到255这个域里面，所以叫域代数。存储文件可以认为是0到255的一个序列，举个例子，一个100K的文件拆成10份，每份是10K，存在10个地方，但文件仍然是一份。这时候用域代数里的加法（其实就是计算机中的异或操作），从这10份数据里取出一份校验数据，数据变成了11份，它的冗余度是1.1。这是一种基于校验码的存储方式，成本比较低，但效果和双副本差不多，其中任何一个数据丢了，都能恢复回去。

• «存储系统的那些事 —-七牛新存储(V2)上线有感 许世伟于2014年6月5日»

新存储的第一大亮点是引入了纠删码(EC)这样的算数冗余方案，而不再是经典的3副本冗余方案。我们的EC采用的是28+4，也就是把文件切分为28份，然后再根据这28份数据计算出4份冗余数据，最后把这32份数据存储在32台不同的计算机上。这样做的好处是既便宜，又提升了可靠性和可用性。从成本角度，同样是要存储1PB的数据，要买的存储服务器只要3副本存储的36.5%,经济效益相当好。从可靠性方面，以前3副本只允许同事损坏2块盘，现在允许同时损坏4块盘，直观来说大大改善了可靠性。从可用性角度，以前能够接受2台服务器下线，现在能否同时允许4台服务器下线。新存储的第二大两点是修复速度，我们把单盘修复时间从三小时提升到了30分钟以内。修复时间对提升可靠性有着重要意义。28+4(M=4)方案保证数据丢失概率是1e-16，即可以做到16个9的可靠性。

    上面一段有待商榷的是，通过36.5%这个经济效益值不知许先生是怎么计算出来的？我认为是38.95%【（28+4）/ (28 * 3) = 38.95%】。

    上面三段引论中，都是我从互联网上搜集来的七牛存储方案的只言片语。可以确认的是，其计算过程一定是基于有限域的纠删码算法。不能确认的是它的纠删码算法，即28+4(M=4)方案【如果按照七牛云存储CTO韩拓的说法，应当是M=28, N=4】中，这4份冗余数据是如何计算出来的？

    大体来说，纠删码的算法有分为XOR码和RS码两类，XOR码基于有限域GF(2)，因其编解码的加法运算基于计算机能够快速完成异或运算（bit-wise exclusive-OR）。常见的XOR码有：

• 低密度奇偶校验码（Low Density Parity Code, LDPC）
• 柯西-里德所罗门码（Cauchy-Reed-Solomon Codes，CRS）
• RAID码（如RAID5、RAID6）
• 奇偶码（EVENODD）
• X-码（X-code）

    从第二段引论，可以确认的是七牛的存储算法应该是基于GF(2^3)有限域，其纠删码算法应该是XOR码算法的一种。其GM应该是4行7列矩阵(矩阵上每个元素亦可视为一个矩阵块，即一份数据分块)，D则应该为7行一列矩阵，其校验矩阵C则应该为四行一列矩阵（每个元素就是一个校验数据块）。

    个人的推算也仅能到此为止。或许随着七牛公司以后披露更多的资料，我继续对这篇文章进行补充。

    以上分析可能谬论百出，还请各位行家抛砖，继续修改本篇文章，以求共同进步。