标签：
网上有很多关于CORDIC算法的资料，看了之后觉得还是wikipedia讲述的更加清晰，特此总结+转载
http://en.wikipedia.org/wiki/CORDIC
算法思想
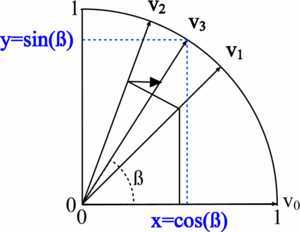
CORDIC算法是一种对目标值进行逼近的迭代算法，且迭代次数越多精度越高。迭代过程中仅仅需要除2运算和加减运算，因此特别适合硬件方式实现。在单位圆中，圆上角β点的x坐标和y坐标分别对应β的cos和sin值，因此，求角β的正弦值的CORDICn次迭代过程如下：
1、以(1,0)为初始点，向靠近β的方向旋转arctan(1)=45°得到点v1
2、v1向靠近β的方向旋转角度arctan(1/2)得到点v2
3、点vi向靠近β的方向旋转角度arctanc(1/(2^i))得到vi+1
4、当i+1=n时，停止，vn的坐标便是所求正余弦值
坐标旋转
每一次cordic迭代都是以此旋转计算，通过让
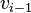乘以旋转矩阵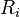
来实现，如下式：
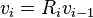
旋转矩阵通过下式来计算：
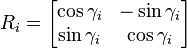
而cos和sin函数可用下式化为tan
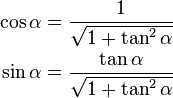
因此
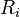可化为：
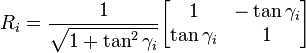
如果让tan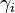
取值
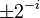，那么vi坐标与矩阵的乘法运算均可用移位来实现，此时旋转公式为：
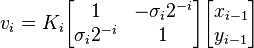
其中，
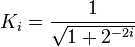
Ki可以在迭代完成后单独计算，最终只需乘以Kn即可：
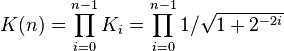
随着n的增加，Kn趋于稳定
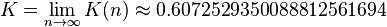
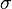取±1，它决定着是顺时针旋转还是逆时针旋转。
β则根据下式进行逼近，每次迭代都应朝着向β靠近的方向旋转。
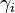的值可以通过查表法来获得。
Matlab 代码
1 function v = cordic(beta,n) 2 % This function computes v = [cos(beta), sin(beta)] (beta in radians) 3 % using n iterations. Increasing n will increase the precision. 4 5 if beta < -pi/2 || beta > pi/2 6 if beta < 0 7 v = cordic(beta + pi, n); 8 else 9 v = cordic(beta - pi, n); 10 end 11 v = -v; % flip the sign for second or third quadrant 12 return 13 end 14 15 % Initialization of tables of constants used by CORDIC 16 % need a table of arctangents of negative powers of two, in radians: 17 % angles = atan(2.^-(0:27)); 18 angles = [ ... 19 0.78539816339745 0.46364760900081 0.24497866312686 0.12435499454676 ... 20 0.06241880999596 0.03123983343027 0.01562372862048 0.00781234106010 ... 21 0.00390623013197 0.00195312251648 0.00097656218956 0.00048828121119 ... 22 0.00024414062015 0.00012207031189 0.00006103515617 0.00003051757812 ... 23 0.00001525878906 0.00000762939453 0.00000381469727 0.00000190734863 ... 24 0.00000095367432 0.00000047683716 0.00000023841858 0.00000011920929 ... 25 0.00000005960464 0.00000002980232 0.00000001490116 0.00000000745058 ]; 26 % and a table of products of reciprocal lengths of vectors [1, 2^-2j]: 27 Kvalues = [ ... 28 0.70710678118655 0.63245553203368 0.61357199107790 0.60883391251775 ... 29 0.60764825625617 0.60735177014130 0.60727764409353 0.60725911229889 ... 30 0.60725447933256 0.60725332108988 0.60725303152913 0.60725295913894 ... 31 0.60725294104140 0.60725293651701 0.60725293538591 0.60725293510314 ... 32 0.60725293503245 0.60725293501477 0.60725293501035 0.60725293500925 ... 33 0.60725293500897 0.60725293500890 0.60725293500889 0.60725293500888 ]; 34 Kn = Kvalues(min(n, length(Kvalues))); 35 36 % Initialize loop variables: 37 v = [1;0]; % start with 2-vector cosine and sine of zero 38 poweroftwo = 1; 39 angle = angles(1); 40 41 % Iterations 42 for j = 0:n-1; 43 if beta < 0 44 sigma = -1; 45 else 46 sigma = 1; 47 end 48 factor = sigma * poweroftwo; 49 R = [1, -factor; factor, 1]; 50 v = R * v; % 2-by-2 matrix multiply 51 beta = beta - sigma * angle; % update the remaining angle 52 poweroftwo = poweroftwo / 2; 53 % update the angle from table, or eventually by just dividing by two 54 if j+2 > length(angles) 55 angle = angle / 2; 56 else 57 angle = angles(j+2); 58 end 59 end 60 61 % Adjust length of output vector to be [cos(beta), sin(beta)]: 62 v = v * Kn; 63 return
标签：
原文地址：http://www.cnblogs.com/huangqiwei/p/4177067.html
