标签:
选择排序的基本思想是:每一趟从n-i+1 (i=1,2,…,n)个元素中选取一个关键字最小的元素作为有序序列中第i个元素。本节在介绍简单选择排序的基础上,给出了对其进行改进的算法堆排序。
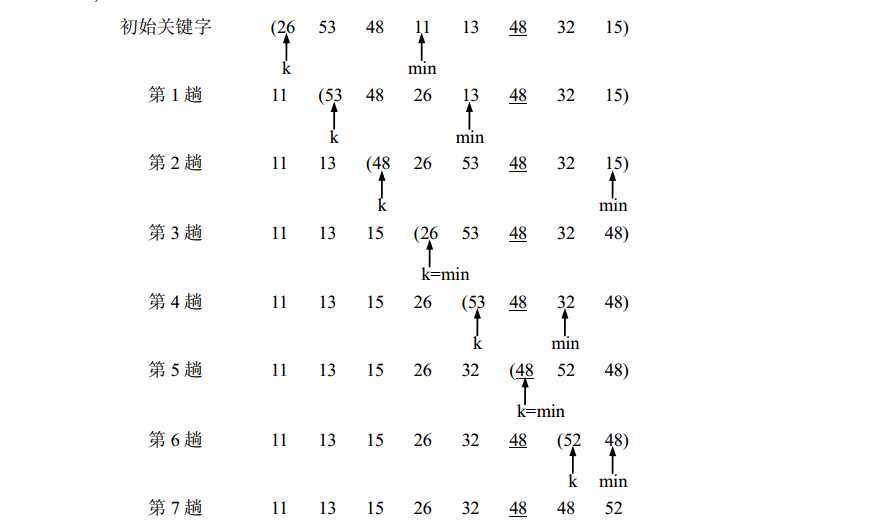
简单选择排序的基本思想非常简单,即:第一趟,从n个元素中找出关键字最小的元素与第一个元素交换;第二趟,在从第二个元素开始的n-1个元素中再选出关键字最小的元素与第二个元素交换;如此,第k趟,则从第k个元素开始的n-k+1个元素中选出关键字最小的元素与第k个元素交换,直到整个序列按关键字有序。
public void selectSort(int[] r, int low, int high) {
for (int k = low; k < high - 1; k++) { // 作n-1趟选取
int min = k;
for (int i = min + 1; i <= high; i++)
// 选择关键字最小的元素
if (compare(r[i], r[min]))
min = i;
if (k != min) {
int temp = r[k]; // 关键字最小的元素与元素r[k]交换
r[k] = r[min];
r[min] = temp;
}// end of if
}// end of for(int k=0…
}// end of selectSort
【效率分析】
空间效率:显然简单选择排序只需要一个辅助空间。
时间效率:在简单选择排序中,所需移动元素的次数较少,在待排序序列已经有序的情况下,简单选择排序不需要移动元素,在最坏的情况下,即待排序序列本身是逆序时,则移动元素的次数为3(n-1)。然而无论简单选择排序过程中移动元素的次数是多少,在任何情况下,简单选择排序都需要进行n(n-1)/2次比较操作,因此简单选择排序的时间复杂度为Ο(n²)
SelectSort.java
package com.test.sort.selection;
public class SelectSort {
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
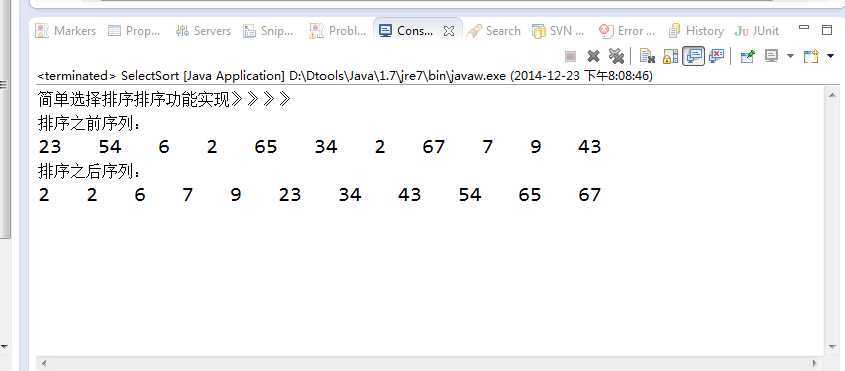
System.out.println("简单选择排序排序功能实现》》》》");
int[] arr = { 23, 54, 6, 2, 65, 34, 2, 67, 7, 9, 43 };
SelectSort sort = new SelectSort();
System.out.println("排序之前序列:");
sort.printArr(arr);
sort.selectSort(arr, 0, arr.length - 1);
System.out.println("排序之后序列:");
;
sort.printArr(arr);
}
public void selectSort(int[] r, int low, int high) {
for (int k = low; k < high - 1; k++) { // 作n-1趟选取
int min = k;
for (int i = min + 1; i <= high; i++)
// 选择关键字最小的元素
if (compare(r[i], r[min]))
min = i;
if (k != min) {
int temp = r[k]; // 关键字最小的元素与元素r[k]交换
r[k] = r[min];
r[min] = temp;
}// end of if
}// end of for(int k=0…
}// end of selectSort
public boolean compare(int paramA, int paramB) {
if (paramA < paramB) {
return true;
} else {
return false;
}
}
/**
* 依次打印出数组元素
*/
public void printArr(int[] arr) {
if (arr != null) {
for (int temp : arr) {
System.out.print(temp + " ");
}
System.out.println();
}
}
}
设有n个元素,欲将其按关键字排序。可以首先将这n个元素按关键字建成堆,将堆顶元素输出,得到n个元素中关键字最大(或最小)的元素。然后,再将剩下的n-1个元素重新建成堆,再输出堆顶元素,得到n个元素中关键字次大(或次小)的元素。如此反复执行,直到最后只剩一个元素,则可以得到一个有序序列,这个排序过程称之为堆排序。堆排序需要解决两个问题,一个是如何将n个元素的序列按关键字建成堆;一个是输出堆顶元素后,怎样调整剩余n-1个元素,使其按关键字成为一个新堆。
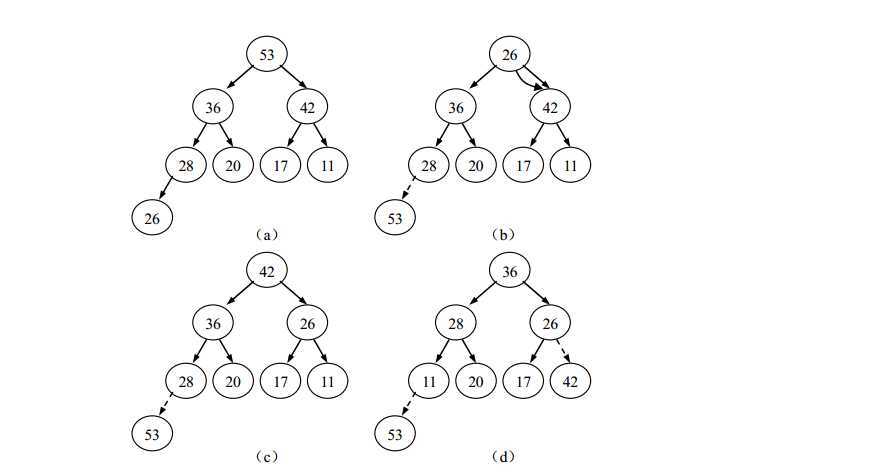
调整堆结构
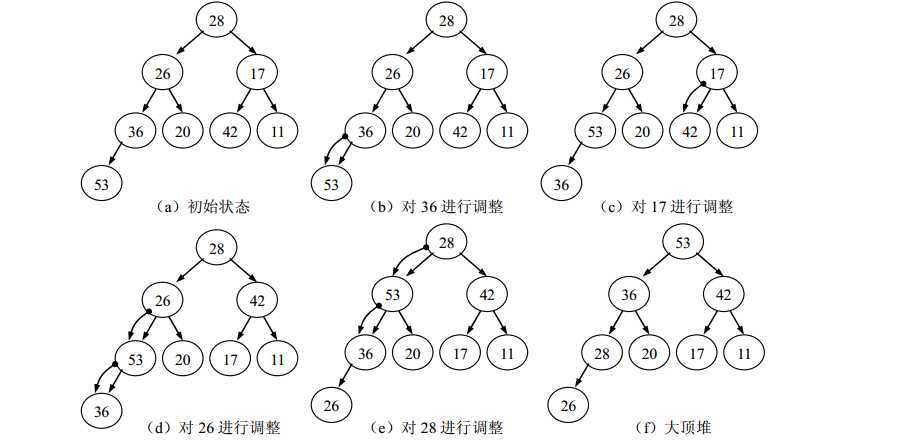
初始堆建立过程
public void heapSort(int[] r) {
int n = r.length - 1;
for (int i = n / 2; i >= 1; i--)
// 初始化建堆
heapAdjust(r, i, n);
for (int i = n; i > 1; i--) { // 不断输出堆顶元素并调整r[1..i-1]为新堆
int temp = r[1]; // 交换堆顶与堆底元素
r[1] = r[i];
r[i] = temp;
heapAdjust(r, 1, i - 1); // 调整
}
}
// 已知r[low..high]中除r[low]之外,其余元素均满足堆的定义
private void heapAdjust(int[] r, int low, int high) {
int temp = r[low];
for (int j = 2 * low; j <= high; j = j * 2) { // 沿关键之较大的元素向下进行筛选
// j指向关键之较大的元素
if (j < high && compare(r[j], r[j + 1]))
j++;
// 若temp比其孩子都大,则插入到low所指位置
if (!compare(temp, r[j]))
break;
r[low] = r[j];
low = j; // 向下筛选
}
r[low] = temp;
}
HeapSort.java
package com.test.sort.selection;
public class HeapSort {
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
System.out.println("堆排序排序功能实现》》》》");
int[] arr = {1, 54, 6, 1, 65, 34, 2, 67, 7, 9, 43 };
HeapSort sort = new HeapSort();
System.out.println("排序之前序列:");
sort.printArr(arr);
sort.heapSort(arr);
System.out.println("排序之后序列:");
sort.printArr(arr);
}
public void heapSort(int[] r) {
int n = r.length - 1;
for (int i = n / 2; i >= 1; i--)
// 初始化建堆
heapAdjust(r, i, n);
for (int i = n; i > 1; i--) { // 不断输出堆顶元素并调整r[1..i-1]为新堆
int temp = r[1]; // 交换堆顶与堆底元素
r[1] = r[i];
r[i] = temp;
heapAdjust(r, 1, i - 1); // 调整
}
}
// 已知r[low..high]中除r[low]之外,其余元素均满足堆的定义
private void heapAdjust(int[] r, int low, int high) {
int temp = r[low];
for (int j = 2 * low; j <= high; j = j * 2) { // 沿关键之较大的元素向下进行筛选
// j指向关键之较大的元素
if (j < high && compare(r[j], r[j + 1]))
j++;
// 若temp比其孩子都大,则插入到low所指位置
if (!compare(temp, r[j]))
break;
r[low] = r[j];
low = j; // 向下筛选
}
r[low] = temp;
}
public boolean compare(int paramA, int paramB) {
if (paramA < paramB) {
return true;
} else {
return false;
}
}
/**
* 依次打印出数组元素
*/
public void printArr(int[] arr) {
if (arr != null) {
for (int temp : arr) {
System.out.print(temp + " ");
}
System.out.println();
}
}
}
标签:
原文地址:http://www.cnblogs.com/zhangminghui/p/4181121.html