标签:
1.引言
假如你经营着一家网店,里面卖各种商品(Items),有很多用户在你的店里面买过东西,并对买过的Items进行了评分,我们称之为历史信息,现在为了提高销售量,必须主动向用户推销产品,所以关键是要判断出用户除了已经买过的商品之外还会喜欢哪些商品,这就需要利用用户购买商品过程产生的历史信息。协同过滤通常分为基于用户的协同过滤和基于商品的协同过滤。
2.原理
关于协同过滤的原理网上到处都有,思想很简单,这里就不赘述,下面举一个简单的实例来说明基于用户的协同过滤:
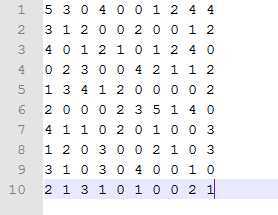
上面每一行代表一个用户,每一列代表一个商品,比如第2行第一列的3表示用户2对商品1的评分为3,0代表对应的用户还没有购买过该商品,现在想预测用户2对商品4的评分:
要计算用户2与用户1之间的相似度,首先找到二者都评过分的商品为:商品1, 2, 9, 10,用户1对这4个商品的评分向量为r1=[5 3 4 4],用户2对这4个商品评分向量为r2=[3 1 1 2];所谓余弦相似度 就是利用两个向量之间夹角的余弦值来衡量两个向量之间的相似度,显然夹角越小,余弦值就越大,两个向量就越靠近,即二者越相似,于是用户2和用户1之间的相似度就为
sim2_1=(5*3 + 3*1 + 4*1 + 4*2)/ (||r1|| * ||r2||) = 0.953, 其中||r||代表向量r的模长或者2范数,类似地分别计算出用户2与用户3 4 8 9 10之间的sim2_3,sim2_5,sim2_8,
sim2_9,sim2_10
3.实现
关于Matlab的实现可以参考:http://blog.csdn.net/google19890102/article/details/28112091,这里我用C++实现,并用movielens.rar进行测试,这个数据集是包括训练集和测试集,已经处理成矩阵形式。
#ifndef LOAD_H
#define LOAD_H
#include <iostream>
#include <fstream>
#include <vector>
#include <string>
using namespace std;
template <typename T>
vector<vector<T> > txtRead(string FilePath,int row,int col)
{
ifstream input(FilePath);
if (!input.is_open())
{
cerr << "File is not existing, check the path: \n" << FilePath << endl;
exit(1);
}
vector<vector<T> > data(row, vector<T>(col,0));
for (int i = 0; i < row; ++i)
{
for (int j = 0; j < col; ++j)
{
input >> data[i][j];
}
}
return data;
}
template<typename T>
void txtWrite(vector<vector<T> > Matrix, string dest)
{
ofstream output(dest);
vector<vector<T> >::size_type row = Matrix.size();
vector<T>::size_type col = Matrix[0].size();
for (vector<vector<T> >::size_type i = 0; i < row; ++i)
{
for (vector<T>::size_type j = 0; j < col; ++j)
{
output << Matrix[i][j];
}
output << endl;
}
}
#endif
1 #ifndef EVALUATE_H
2 #define EVALUATE_H
3 #include <cmath>
4 #include <vector>
5
6 double ComputeRMSE(vector<vector<double> > predict, vector<vector<double> > test)
7 {
8 int Counter = 0;
9 double sum = 0;
10 for (vector<vector<double> >::size_type i = 0; i < test.size(); ++i)
11 {
12 for (vector<double>::size_type j = 0; j < test[0].size(); ++j)
13 {
14 if (predict[i][j] && test[i][j])
15 {
16 ++Counter;
17 sum += pow((test[i][j] - predict[i][j]), 2);
18 }
19 }
20 }
21 return sqrt(sum / Counter);
22 }
23
24 #endif
1 #include "load.h"
2 #include "evaluate.h"
3 #include <vector>
4 #include <string>
5 #include <cmath>
6 #include <assert.h>
7 using namespace std;
8
9 double norm(vector<double> A)
10 {
11 double res = 0;
12 for(vector<double>::size_type i = 0; i < A.size(); ++i)
13 {
14 res += pow(A[i], 2);
15 }
16 return sqrt(res);
17 }
18
19 double InnerProduct(vector<double> A, vector<double> B)
20 {
21 double res = 0;
22 for(vector<double>::size_type i = 0; i < A.size(); ++i)
23 {
24 res += A[i] * B[i];
25 }
26 return res;
27 }
28
29 double ComputeSim(vector<double> A, vector<double> B, int method)
30 {
31 switch (method)
32 {
33 case 0://欧氏距离
34 {
35 vector<double> C;
36 for(vector<double>::size_type i = 0; i < A.size(); ++i)
37 {
38 C.push_back((A[i] - B[i]));
39 }
40 return 1 / (1 + norm(C));
41 break;
42 }
43 case 1://皮尔逊相关系数
44 {
45 double A_mean = 0;
46 double B_mean = 0;
47 for(vector<double>::size_type i = 0; i < A.size(); ++i)
48 {
49 A_mean += A[i];
50 B_mean += B[i];
51 }
52 A_mean /= A.size();
53 B_mean /= B.size();
54 vector<double> C(A);
55 vector<double> D(B);
56 for(vector<double>::size_type i = 0; i < A.size(); ++i)
57 {
58 C[i] = A[i] - A_mean;
59 D[i] = B[i] - B_mean;
60 }
61 assert(norm(C) * norm(D));
62 return InnerProduct(C,D) / (norm(C) * norm(D));
63 break;
64 }
65 case 2:
66 {
67 assert(norm(A) * norm(B));
68 return InnerProduct(A,B) / (norm(A) * norm(B));
69 break;
70 }
71 default:
72 {
73 cout << " Choose method:" << endl;
74 cout << "0:欧氏距离\n1:皮尔逊相关系数\n2:余弦相似度\n";
75 return -1;
76 }
77 }
78
79 }
80
81 void FindCommon(vector<double> A, vector<double> B, vector<double> &C, vector<double> &D)
82 {
83 for(vector<double>::size_type i = 0; i < A.size(); ++i)
84 {
85 if (A[i] && B[i])
86 {
87 C.push_back(A[i]);
88 D.push_back(B[i]);
89 }
90 }
91 }
92
93
94 vector<vector<double> > UserBasedCF(vector<vector<double> > train, int usersNum, int itemsNum)
95 {
96 vector<vector<double> > predict(usersNum, vector<double>(itemsNum, 0));
97 for (int i = 0; i < usersNum; ++i) //对每个用户进行预测
98 {
99 //找出user i未评分的item j,预测user i 对item j的评分
100 for (int j = 0; j < itemsNum; ++j)
101 {
102
103
104 if (train[i][j])
105 continue;
106 //如果item j没有被user i评过分,找出对 item j评过分的用户
107 else
108 {
109 vector<double> sim;
110 vector<double> historyScores;
111 for (int k = 0; k < usersNum; ++k)
112 {
113 //如果user k对item j 评过分,计算user k与user i的相似度
114
115 if (train[k][j])//找出对item j 评过分的user k
116 {
117 // 为了计算user k与user i的相似度,必须找出二者共同评过分的items
118 // 把二者对共同评过分的items的评分分别存储在两个vector中
119 vector<double> commonA,commonB;
120 FindCommon(train[i], train[k], commonA, commonB);
121 //如果二者存在共同评过分的items,计算相似度
122 if (!commonA.empty())
123 {
124 sim.push_back(ComputeSim(commonA, commonB, 2));
125 // 把user k对item j 的历史评分记录下来
126 historyScores.push_back(train[k][j]);
127 }
128 }
129
130 }
131 // 计算出所有与user i存在共同评过分的items的users与user i之间的相似度,
132 // 保存在sim中,这些users对目标items j(即user i没有评过分)的历史评分记
133 // 录在historyScores中。利用这两个vector,计算出相似度加权平均分作为预
134 // 测user i对item j的评分
135 double SimSum = 0;
136 if (!sim.empty())
137 {
138 for(vector<double>::size_type m = 0; m < sim.size(); ++m)
139 {
140 SimSum += sim[m];
141 }
142 predict[i][j] = InnerProduct(sim, historyScores) / (SimSum);
143 cout << "User "<< i << " 对第 " << j << " 个Item的评分为 " << predict[i][j] << endl;
144 }
145 }
146 }
147 }
148 return predict;
149 }
150
151 int main()
152 {
153 string FilePath1("E:\\Matlab code\\recommendation system\\data\\movielens\\train.txt");
154 string FilePath2("E:\\Matlab code\\recommendation system\\data\\movielens\\test.txt");
155
156 int row = 943;
157 int col = 1682;
158 vector<vector<double> > train = txtRead<double>(FilePath1, row, col);
159 vector<vector<double> > predict = UserBasedCF(train, row, col);
160 txtWrite(predict, "predict.txt");
161 vector<vector<double> > test = txtRead<double>(FilePath2, 462, 1591);
162 double rmse = ComputeRMSE(predict,test);
163 cout << "RMSE is " << rmse <<endl;
164 return 0;
165 }
4.运行
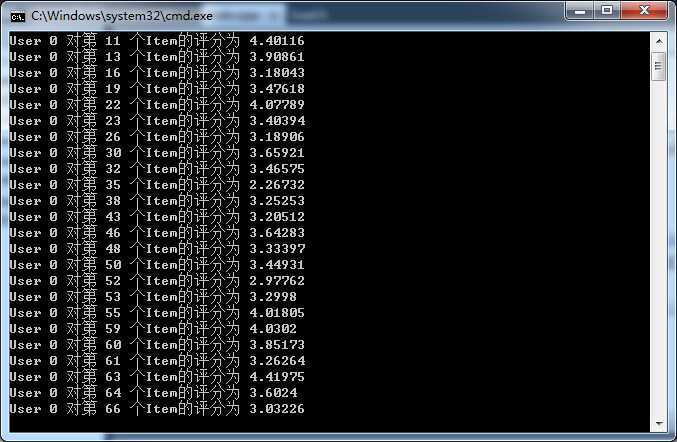
由于程序没有优化,循环比较多,时间比较长,程序没写好,如果读者有兴趣帮我优化,请联系我,多谢,欢迎有兴趣的可以自己构造一个小点的数据集试一试,以前我用这个数据在Matlab中运行的RMSE是1左右,所以如果读者运行结果得到测试集上的RMSE是0.9-1.3之间问题应该不大,如果偏离太多,程序设计可能就有问题。
标签:
原文地址:http://www.cnblogs.com/90zeng/p/CollabirativeFiltering.html