.NET下文本相似度算法余弦定理和SimHash浅析及应用

时间：2014-12-25 01:23:26 阅读：506 评论：0 收藏：0 [点我收藏+]

标签：

在数据采集及大数据处理的时候，数据排重、相似度计算是很重要的一个环节，由此引入相似度计算算法。常用的方法有几种：最长公共子串（基于词条空间）、最长公共子序列（基于权值空间、词条空间）、最少编辑距离法（基于词条空间）、汉明距离（基于权值空间）、余弦值（基于权值空间）等，今天我们着重介绍最后两种方式。

余弦相似性

原理：首先我们先把两段文本分词，列出来所有单词，其次我们计算每个词语的词频，最后把词语转换为向量，这样我们就只需要计算两个向量的相似程度.

我们简单表述如下

文本1：我/爱/北京/天安门/ 经过分词求词频得出向量（伪向量） [1,1,1,1]

文本2：我们/都爱/北京/天安门/ 经过分词求词频得出向量（伪向量） [1,0,1,2]

我们可以把它们想象成空间中的两条线段，都是从原点（[0, 0, ...]）出发，指向不同的方向。两条线段之间形成一个夹角，如果夹角为0度，意味着方向相同、线段重合；如果夹角为90度，意味着形成直角，方向完全不相似；如果夹角为180度，意味着方向正好相反。因此，我们可以通过夹角的大小，来判断向量的相似程度。夹角越小，就代表越相似。

C#核心算法

    public class TFIDFMeasure
    {
        private string[] _docs;
        private string[][] _ngramDoc;
        private int _numDocs=0;
        private int _numTerms=0;
        private ArrayList _terms;
        private int[][] _termFreq;
        private float[][] _termWeight;
        private int[] _maxTermFreq;
        private int[] _docFreq;


        public class TermVector
        {        
            public static float ComputeCosineSimilarity(float[] vector1, float[] vector2)
            {
                if (vector1.Length != vector2.Length)                
                    throw new Exception("DIFER LENGTH");
                

                float denom=(VectorLength(vector1) * VectorLength(vector2));
                if (denom == 0F)                
                    return 0F;                
                else                
                    return (InnerProduct(vector1, vector2) / denom);
                
            }

            public static float InnerProduct(float[] vector1, float[] vector2)
            {
            
                if (vector1.Length != vector2.Length)
                    throw new Exception("DIFFER LENGTH ARE NOT ALLOWED");
                
            
                float result=0F;
                for (int i=0; i < vector1.Length; i++)                
                    result += vector1[i] * vector2[i];
                
                return result;
            }
        
            public static float VectorLength(float[] vector)
            {            
                float sum=0.0F;
                for (int i=0; i < vector.Length; i++)                
                    sum=sum + (vector[i] * vector[i]);
                        
                return (float)Math.Sqrt(sum);
            }

        }

        private IDictionary _wordsIndex=new Hashtable() ;

        public TFIDFMeasure(string[] documents)
        {
            _docs=documents;
            _numDocs=documents.Length ;
            MyInit();
        }

        private void GeneratNgramText()
        {
            
        }

        private ArrayList GenerateTerms(string[] docs)
        {
            ArrayList uniques=new ArrayList() ;
            _ngramDoc=new string[_numDocs][] ;
            for (int i=0; i < docs.Length ; i++)
            {
                Tokeniser tokenizer=new Tokeniser() ;
                string[] words=tokenizer.Partition(docs[i]);            

                for (int j=0; j < words.Length ; j++)
                    if (!uniques.Contains(words[j]) )                
                        uniques.Add(words[j]) ;
                                
            }
            return uniques;
        }
        


        private static object AddElement(IDictionary collection, object key, object newValue)
        {
            object element=collection[key];
            collection[key]=newValue;
            return element;
        }

        private int GetTermIndex(string term)
        {
            object index=_wordsIndex[term];
            if (index == null) return -1;
            return (int) index;
        }

        private void MyInit()
        {
            _terms=GenerateTerms (_docs );
            _numTerms=_terms.Count ;

            _maxTermFreq=new int[_numDocs] ;
            _docFreq=new int[_numTerms] ;
            _termFreq =new int[_numTerms][] ;
            _termWeight=new float[_numTerms][] ;

            for(int i=0; i < _terms.Count ; i++)            
            {
                _termWeight[i]=new float[_numDocs] ;
                _termFreq[i]=new int[_numDocs] ;

                AddElement(_wordsIndex, _terms[i], i);            
            }
            
            GenerateTermFrequency ();
            GenerateTermWeight();            
                
        }
        
        private float Log(float num)
        {
            return (float) Math.Log(num) ;//log2
        }

        private void GenerateTermFrequency()
        {
            for(int i=0; i < _numDocs  ; i++)
            {                                
                string curDoc=_docs[i];
                IDictionary freq=GetWordFrequency(curDoc);
                IDictionaryEnumerator enums=freq.GetEnumerator() ;
                _maxTermFreq[i]=int.MinValue ;
                while (enums.MoveNext())
                {
                    string word=(string)enums.Key;
                    int wordFreq=(int)enums.Value ;
                    int termIndex=GetTermIndex(word);

                    _termFreq [termIndex][i]=wordFreq;
                    _docFreq[termIndex] ++;

                    if (wordFreq > _maxTermFreq[i]) _maxTermFreq[i]=wordFreq;                    
                }
            }
        }
        

        private void GenerateTermWeight()
        {            
            for(int i=0; i < _numTerms   ; i++)
            {
                for(int j=0; j < _numDocs ; j++)                
                    _termWeight[i][j]=ComputeTermWeight (i, j);                
            }
        }

        private float GetTermFrequency(int term, int doc)
        {            
            int freq=_termFreq [term][doc];
            int maxfreq=_maxTermFreq[doc];            
            
            return ( (float) freq/(float)maxfreq );
        }

        private float GetInverseDocumentFrequency(int term)
        {
            int df=_docFreq[term];
            return Log((float) (_numDocs) / (float) df );
        }

        private float ComputeTermWeight(int term, int doc)
        {
            float tf=GetTermFrequency (term, doc);
            float idf=GetInverseDocumentFrequency(term);
            return tf * idf;
        }
        
        private  float[] GetTermVector(int doc)
        {
            float[] w=new float[_numTerms] ;
            for (int i=0; i < _numTerms; i++)                                            
                w[i]=_termWeight[i][doc];
            
                
            return w;
        }

        public float GetSimilarity(int doc_i, int doc_j)
        {
            float[] vector1=GetTermVector (doc_i);
            float[] vector2=GetTermVector (doc_j);

            return TermVector.ComputeCosineSimilarity(vector1, vector2) ;

        }
        
        private IDictionary GetWordFrequency(string input)
        {
            string convertedInput=input.ToLower() ;
                    
            Tokeniser tokenizer=new Tokeniser() ;
            String[] words=tokenizer.Partition(convertedInput);            
            Array.Sort(words);
            
            String[] distinctWords=GetDistinctWords(words);
                        
            IDictionary result=new Hashtable();
            for (int i=0; i < distinctWords.Length; i++)
            {
                object tmp;
                tmp=CountWords(distinctWords[i], words);
                result[distinctWords[i]]=tmp;
                
            }
            
            return result;
        }                
                
        private string[] GetDistinctWords(String[] input)
        {                
            if (input == null)            
                return new string[0];            
            else
            {
                ArrayList list=new ArrayList() ;
                
                for (int i=0; i < input.Length; i++)
                    if (!list.Contains(input[i])) // N-GRAM SIMILARITY?                
                        list.Add(input[i]);
                
                return Tokeniser.ArrayListToArray(list) ;
            }
        }
        

        
        private int CountWords(string word, string[] words)
        {
            int itemIdx=Array.BinarySearch(words, word);
            
            if (itemIdx > 0)            
                while (itemIdx > 0 && words[itemIdx].Equals(word))                
                    itemIdx--;                
                        
            int count=0;
            while (itemIdx < words.Length && itemIdx >= 0)
            {
                if (words[itemIdx].Equals(word)) count++;                
                
                itemIdx++;
                if (itemIdx < words.Length)                
                    if (!words[itemIdx].Equals(word)) break;                    
                
            }
            
            return count;
        }                
    }

View Code

缺点

由于有可能一个文章的特征向量词特别多导致整个向量维度很高，使得计算的代价太大不适合大数据量的计算。

SimHash

原理

算法的主要思想是降维，将高维的特征向量映射成一个f-bit的指纹(fingerprint)，通过比较两篇文章的f-bit指纹的Hamming Distance来确定文章是否重复或者高度近似。由于每篇文章我们都可以事先计算好Hamming Distance来保存，到时候直接通过Hamming Distance来计算，所以速度非常快适合大数据计算。

Google就是基于此算法实现网页文件查重的。我们假设有以下三段文本：

1，the cat sat on the mat

2，the cat sat on a mat

3，we all scream for ice cream

如何实现这种hash算法呢？以上述三个文本为例，整个过程可以分为以下六步：
1、选择simhash的位数，请综合考虑存储成本以及数据集的大小，比如说32位
2、将simhash的各位初始化为0
3、提取原始文本中的特征，一般采用各种分词的方式。比如对于"the cat sat on the mat"，采用两两分词的方式得到如下结果：{"th", "he", "e ", " c", "ca", "at", "t ", " s", "sa", " o", "on", "n ", " t", " m", "ma"}
4、使用传统的32位hash函数计算各个word的hashcode，比如："th".hash = -502157718
，"he".hash = -369049682，……
5、对各word的hashcode的每一位，如果该位为1，则simhash相应位的值加1；否则减1
6、对最后得到的32位的simhash，如果该位大于1，则设为1；否则设为0

流程图如下

技术分享

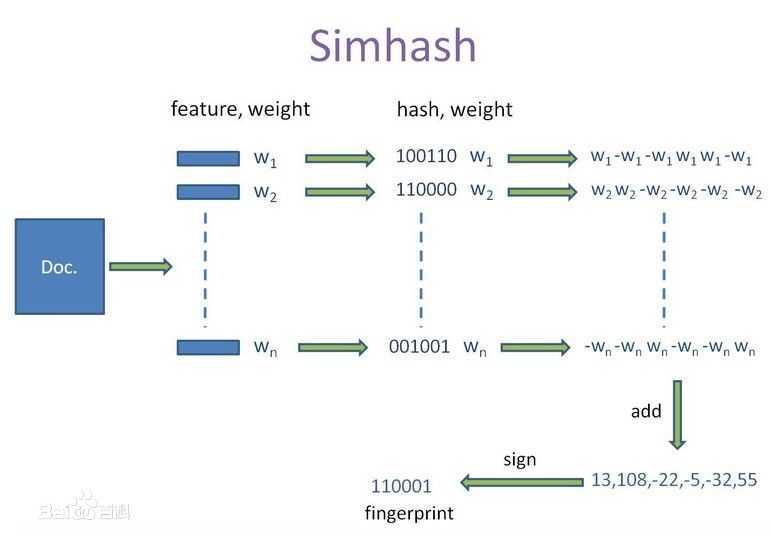
按照Charikar在论文中阐述的，64位simhash，海明距离在3以内的文本都可以认为是近重复文本。当然，具体数值需要结合具体业务以及经验值来确定.

c#核心算法

 1 public class SimHashAnalyser : IAnalyser
 2     {
 3         #region Constants and Fields
 4 
 5         private const int HashSize = 32;
 6 
 7         #endregion
 8 
 9         #region Public Methods and Operators
10 
11         public float GetLikenessValue(string needle, string haystack)
12         {
13             var needleSimHash = this.DoCalculateSimHash(needle);
14             var hayStackSimHash = this.DoCalculateSimHash(haystack);
15             return (HashSize - GetHammingDistance(needleSimHash, hayStackSimHash)) / (float)HashSize;
16         }
17 
18         #endregion
19 
20         #region Methods
21 
22         private static IEnumerable<int> DoHashTokens(IEnumerable<string> tokens)
23         {
24             var hashedTokens = new List<int>();
25             foreach (string token in tokens)
26             {
27                 hashedTokens.Add(token.GetHashCode());
28             }
29             return hashedTokens;
30         }
31 
32         private static int GetHammingDistance(int firstValue, int secondValue)
33         {
34             var hammingBits = firstValue ^ secondValue;
35             var hammingValue = 0;
36             for (int i = 0; i < 32; i++)
37             {
38                 if (IsBitSet(hammingBits, i))
39                 {
40                     hammingValue += 1;
41                 }
42             }
43             return hammingValue;
44         }
45 
46         private static bool IsBitSet(int b, int pos)
47         {
48             return (b & (1 << pos)) != 0;
49         }
50 
51         private int DoCalculateSimHash(string input)
52         {
53             ITokeniser tokeniser = new OverlappingStringTokeniser(4, 3);
54             var hashedtokens = DoHashTokens(tokeniser.Tokenise(input));
55             var vector = new int[HashSize];
56             for (var i = 0; i < HashSize; i++)
57             {
58                 vector[i] = 0;
59             }
60 
61             foreach (var value in hashedtokens)
62             {
63                 for (var j = 0; j < HashSize; j++)
64                 {
65                     if (IsBitSet(value, j))
66                     {
67                         vector[j] += 1;
68                     }
69                     else
70                     {
71                         vector[j] -= 1;
72                     }
73                 }
74             }
75 
76             var fingerprint = 0;
77             for (var i = 0; i < HashSize; i++)
78             {
79                 if (vector[i] > 0)
80                 {
81                     fingerprint += 1 << i;
82                 }
83             }
84             return fingerprint;
85         }
86 
87         #endregion
88     }

View Code

缺点

SimHash对于短文本误判率比较高，因此建议大于500字以上的使用此算法

测试

技术分享

总结

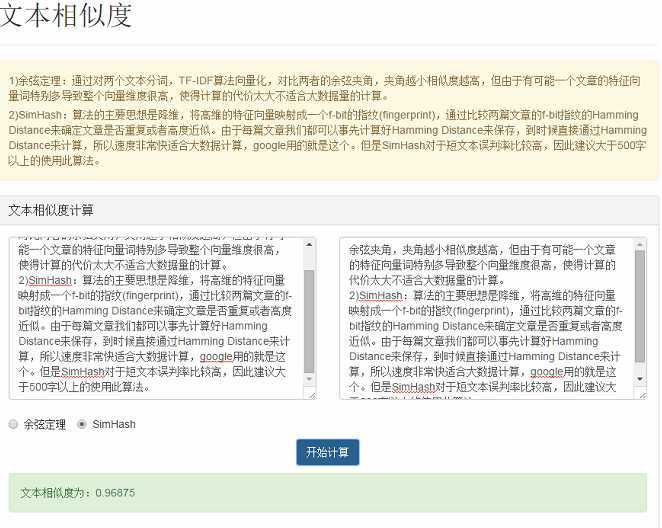
经过大量测试发现，余弦定理和SimHash都能很好的计算出文本相似度，而且有很高的正确度，余弦定理由于要对一整篇文章计算特征向量导致向量维度很高，计算速度比较慢，不适合大数据量的相似度计算；SimHash则事先把每篇文章降维到一个局部哈希数字，计算相似度的时候只需要计算对应的hash值，因此速度比较快，但是测试发现对于短文不误判率比较高，因此建议大于500字以上的使用此算法。

参考

http://grunt1223.iteye.com/blog/964564

http://www.ruanyifeng.com/blog/2013/03/cosine_similarity.html

https://simhash.codeplex.com/

https://github.com/primaryobjects/TFIDF

文章出处:http://www.cnblogs.com/weiguang3100/

.NET 开发交流